1.2 Для одного точечного заряда вне поверхности
Совершенно аналогичные рассуждения, проведенные для случая, когда q находится вне области, ограничиваемой поверхностью S, с учетом знака при подсчете потока через каждую площадку, дают в результате поток ноль. (малый телесный угол теперь пересечет S четное число раз, потоки будут равны по абсолютной величине, но противоположны по знаку)[15].
Суммирование элементарных потоков производится также аналогично сделанному в пункте 1, как и их вычисление.
Итак, для одного заряда вне замкнутой поверхности поток через неё ноль.
2. Для любого количества зарядов
Завершающий шаг прост. Он заключается в применении принципа суперпозиции.
Если для каждого точечного заряда поле , создаваемое им (когда остальные заряды отсутствуют), создает через поверхность поток, удовлетворяющий теореме Гаусса (то есть для каждого заряда внутри поверхности, и 0 для каждого снаружи поверхности), то поток от суммарного поля
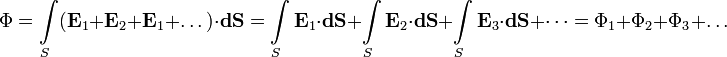
равен сумме потоков, создаваемых каждым зарядом при отсутствии остальных, равен просто
где суммирование производится только по зарядам внутри поверхности (каждый из тех, что снаружи, дает вклад 0).
Теорема доказана.
Доказательство через формулу Гаусса — Остроградского
Это доказательство более формальное.
1. Исходим опять из закона Кулона (в этом параграфе будем использовать систему СГС и говорить для определенности о теореме поле E, а не D):
2. Кулоновское поле удовлетворяет дифференциальной форме закона Гаусса:
Это можно проверить[16] прямой подстановкой[17] формулы (1) в (2).
3. Исходя из принципа суперпозиции полагаем, что поле, создаваемое многими зарядами, также удовлетворяет этому дифференциальному уравнению (попутно замечая, что уравнение это линейное, а следовательно принцип суперпозиции применим).
4. Пользуясь формулой Гаусса — Остроградского, сразу получаем:
Теорема доказана.
См. урок 73-74 в тетради.
Тот же урок.
И снова тот же.
…