На «3»

1. Элементарный заряд – количественная характеристика способности тела к электрическому взаимодействию.

e=1,6*10^-19 Кл

Способы электризации тел: трение, фотоэффект, термоэлектрическая эмиссия, влияние.

2. Закон Кулона: F=(k*|q1|*|q2|)/(r^2); k=9*10^9 H*м^2/Кл^2; E0 = 8,82*10^12 Кл^2/(Н*м^2)

Пределы применимости: точечные заряды, сферически симметричное распределение зарядов, небольшие расстояния.

Векторная форма: F=(k*q1*q2)/r^3*r¯, где r¯ - вектор

3. Закон сохранения электрического заряда: в замкнутых системах (где нет притока/оттока заряда) =const

4. Электрическое поле – особая форма материи, обладающей 2 свойствами: действует на электрический заряд с силой; создаётся электрическим зарядом.

5. Напряженность электрического поля - E¯(x, y, z) = F¯/qпр.

Если напряженность поля E¯ известна, то можно предсказать силу, которая подействует на любой заряд Q.

6. Напряженность поля точечного заряда: E(r¯)=kq/(r^2)

F¯ = k*q1*q2*r¯/r^3 = q2*E¯1(r¯)

7. …

8. Принцип суперпозиции: E¯A= A

Прямой метод: E¯A=F¯Q/Q= ( Q) /Q (?)

9. Силовые линии – линии, касательные к которым совпадают с E¯. Чтобы увидеть направление напряженности электрического поля в данной точке, нужно провести касательную к силовым линиям в данной точке. Чтобы оценить относительную величину вектора напряженности в данной точке, нужно посмотреть на частоту силовых линий в данной точке.

10. 

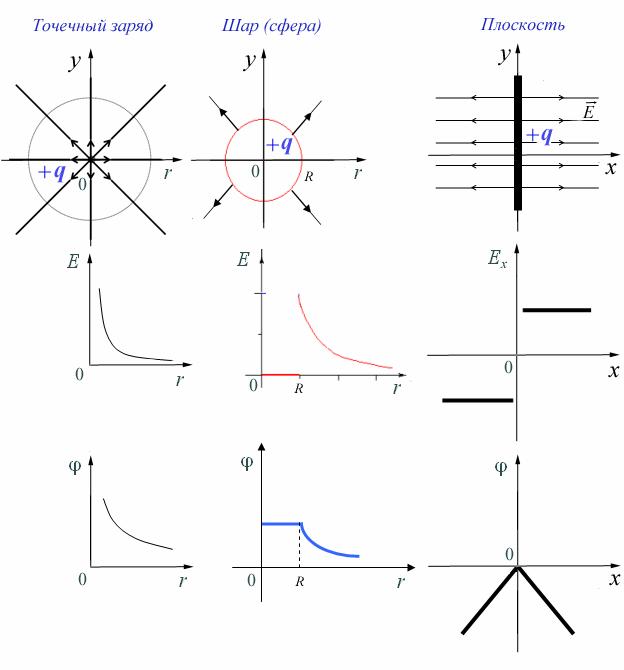
11. E(точечн. заряд) = kq/(R^2)

E(плоскость) = сигма/(2E0)

E(шар_in)=ро/(3E0) ; E(шар_out)=kq/(R^2)

Е(сфера_in) = 0; E(сфера_out)=kq/(R^2)

12. В пределах малой площадки электрическое поле можно считать однородным ^[1], тогда поток вектора напряженности ΔФ_E определяется как произведение площади площадки на нормальную составляющую вектора напряженности

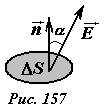
\(~\Delta \Phi_E = E \cos \alpha \Delta S = (\vec E \cdot \vec n) \Delta S = E_n \Delta S\) . (1)

где \(~(\vec E \cdot \vec n) = E \cos \alpha\) — скалярное произведение векторов \(~\vec E\) и \(~\vec n\); E_n — нормальная к площадке компонента вектора напряженности.

В произвольном электростатическом поле поток вектора напряженности через произвольную поверхность, определяется следующим образом (рис. 158):

- поверхность разбивается на малые площадки ΔS (которые можно считать плоскими);

- определяется вектор напряженности \(~\vec E\) на этой площадке (который в пределах площадки можно считать постоянным);

- вычисляется сумма потоков через все площадки, на которые разбита поверхность

\(~\Phi = \Delta \Phi_1 + \Delta \Phi_2 + \Delta \Phi_3 + \ldots = \sum_{i} {\Delta \Phi_i} = \sum_{i} {E_i \cos \alpha_i \Delta S_i}\) .

Эта сумма называется потоком вектора напряженности электриче-ского поля через заданную поверхность.

13. Теорема Остроградского – Гаусса (теорема Гаусса): поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на : .

Таким образом, чтобы рассчитать поле, созданное какой-то конфигурацией зарядов в данной точке, нужно через эту точку провести замкнутую поверхность произвольной формы и рассчитать поток вектора напряженности через эту поверхность. Так как по теореме Гаусса поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на , то, зная величину заряда, находящегося внутри замкнутой поверхности можно найти напряженность поля в интересующей нас точке пространства.

14. Электростатическое поле потенциально. Работа не зависит от пройденного пути => А=W1-W2; A= (фи1-фи2)*q

15. Потенциал электростатического поля – скалярная энергетическая характеристика поля, характеризующая потенциальную энергию поля, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.

16. Потенциальная энергия взаимодействия двух точечных зарядов: U = k*q1*q2/r

17. Разность потенциалов – отношение работы поля по перемещению q из 1 в 2 к заряду q. Если известна разность потенциалов, то можно узнать, какую работу необходимо совершить для перемещения любого заряда q из одной точки в другую.

18. Дельта фи =- E¯ * дельта r¯. Поверхности равного потенциала называются эквипотенциальными поверхностями.

19. См. 10

20. Классическая модель металлического проводника – модель проводника, в которой выполняются законы классической электронной теории (т.е. молекулы подчиняются законам механики Ньютона).

21. Утв. 1: Существуют проводники и диэлектрики.

Утв. 2: Незаряженный проводник всегда притягивается к заряду.

Утв. 3: В статическом состоянии поле внутри проводника равно нулю.

Утв. 4: В статическом состоянии объемная плотность заряда внутри проводника равна нулю.

Утв. 5: Если заряд проводника не равен нулю, то весь заряд расположен на поверхности проводника.

Утв. 6: В статическом состоянии потенциал проводника равен нулю.

Утв. 7: Линии электростатического поля вблизи поверхности проводника перпендикулярны к его поверхности.

Утв. 8: Напряженность поля вблизи поверхности проводника Е = сигма/ Е0

Утв. 9: Максимальная поверхностная плотность заряда достигается в местах самой большой кривизны проводника.

22. Электрический диполь – система, состоящая из двух точечных зарядов, одинаковых по величине и противоположных по знаку, расположенных на малом расстоянии друг от друга.

23. Дипольный момент: p¯=q+*d¯

Опр.: векторная величина, характеризующая, наряду с суммарным зарядом, электрические свойства системы заряженных частиц в смысле создаваемого ею поля и действия на нее внешних полей.

Картина силовых линий – два точечных заряда.

24. Полярные диэлектрики – диэлектрики, в которых центры распределения положительных и отрицательных зарядов совпадают.

Неполярные диэлектрики - диэлектрики, в которых центры распределения положительных и отрицательных зарядов не совпадают.

Явление поляризации диэлектриков – внешнее поле упорядочивает положительные и отрицательные заряды в диэлектрике (плюсы – в одну сторону, минусы – в другую).

25. Ослабление внешнего поля диэлектриками – за счет поляризации (образование внутреннего электрического поля).

Диэлектрическая проницаемость среды – физическая величина, характеризующая свойства изолирующей (диэлектрической) среды и показывающая зависимость электрической индукции от напряжённости электрического поля.

Е = Е0/E

26. Электроёмкость уединенного проводника – физическая величина, характеризующая способность проводников накапливать электрические заряды, а следовательно, и электроэнергию, которая в дальнейшем может быть использована.

С=Q/фи

Электроёмкость изолированного проводящего шара: С = r/k

C=q/фи(q) = q/(k*r/q)=r/k

27. Конденсатор – система двух проводников, расстояние между которыми много меньше их линейных размеров.

Ёмкость конденсатора: С = q+/(фи+ - фи-)

Ёмкость плоского конденсатора: C = E0*S/d

C = q+/U = q+*E0*S/(q+*d) = E0*S/d

28. Ёмкость при параллельном соединении конденсаторов: Сeff =

Ёмкость при последоватльном соединении конденсаторов: 1/Ceff = 1/C1+1/C2+…+1/Ci

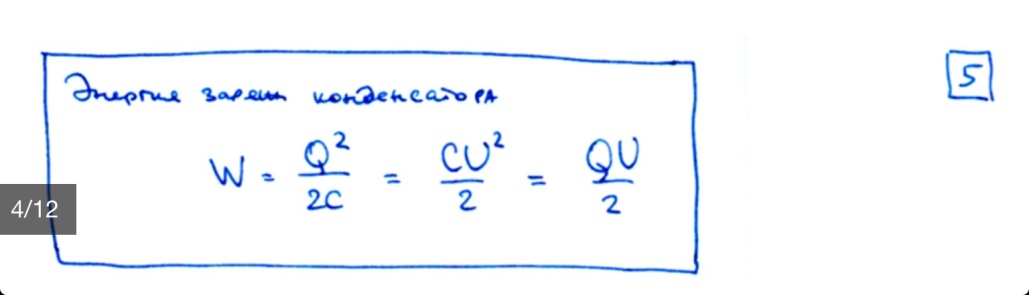
29. Энергия заряженного уединенного проводника – работа по собиранию заряда Q из бесконечности на проводник.

W=Q^2/(2C)=C*U^2/2=Q*U/2

На «4»

1. Поле, образованное двумя разноименными заряженными плоскостями (бесконечно большими)

Поле двух параллельных бесконечно больших плоскостей, заряженных разноименно с одинаковой по величине постоянной поверхностной плотностью можно рассматривать как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. В области между плоскостями (рис.2.13) складываемые поля имеют одинаковое направление, так что результирующая напряженность равна ( 4) Вн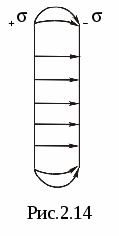 е объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулю E=0. Таким образом, поле сосредоточено между плоскостями. Напряженность поля во всех точках этой области одинакова по величине и по направлению. Поле, обладающее такими свойствами, называется однородным. Линии напряженности однородного поля представляют собой совокупность параллельных равноотстоящих прямых. Поле объемного заряженного шара Найдем напряженность поля, созданного заряженным шаром в точке А, находящейся на расстоянии r от центра шара. Окружим заряженное тело замкнутой сферической поверхностью, радиуса r, проходящей через точку А (рис. 2.18). Для всех точек этой поверхности . Внутрь поверхности попадает весь заряд q, создающий рассматриваемое поле. Следовательно, (так как ). Таким образом, для поля вне шара радиусом R (рисунок 2.18) получается тот же результат, что и для сферы, т.е. справедлива формула: . 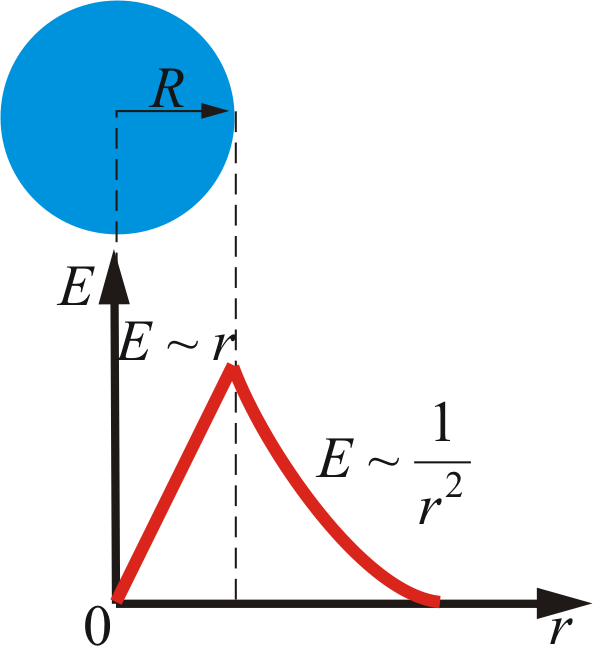Рисунок 2.18 Точка В находится внутри заряженной сферической поверхности, на расстоянии r от центра (r<R). Сферическая поверхность, проведенная через эту точку содержать в себе заряд, равный где ρ – объемная плотность заряда, равная ; – объем шара. Тогда по теореме Остроградского-Гаусса запишем: , т.е. внутри шара . (10) Таким образом, внутри шара напряженность поля пропорциональна расстоянию от центра

Поле, образованное заряженной сферической поверхностью

Ра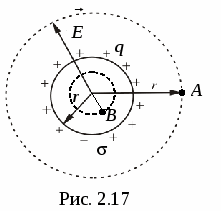 ссмотрим поле, создаваемое сферической поверхностью радиуса R, заряженной с постоянной поверхностной плотностью . Это поле обладает центральной симметрией. Это означает, что направление вектора в любой точке проходит через центр сферы, а значение напряженности является функцией расстояния r от центра сферы (рис. 2.17). Найдем напряженность поля, созданную заряженной сферой в точках А и В. Через точки А и В проведем сферические поверхности и найдем поток вектора напряженности через эти поверхности. Точка В находится внутри заряженной сферической поверхности, на расстоянии r от центра (r<R). Сферическая поверхность, проведенная через эту точку, не будет содержать внутри заряда. Следовательно, по теореме Гаусса , напряженность в точке В будет равна нулю. Е=0 (r<R) (рис. 2.17). Найдем напряженность поля, созданного заряженной сферической поверхностью в точке А, находящейся на расстоянии r от центра сферы. Окружим заряженное тело замкнутой сферической поверхностью, радиуса r, проходящей через точку А (рис. 2.17). Для всех точек этой поверхности . Внутрь поверхности попадает весь заряд q, создающий рассматриваемое поле. Следовательно, (так как ). Таким образом, напряженность поля в точках, расположенных на расстоянии r>R, равна (8) Поле вне заряженной сферической поверхности имеет такой же вид, как поле точечного заряда q, находящегося на расстоянии r от точки А. Если известна поверхностная плотность заряда σ, то , подставив в (8), получим . (9) Поле, образованное бесконечно длинным заряженным цилиндром Ра ссчитаем напряженность поля, создаваемого бесконечно длинным цилиндром радиуса R, заряженным с поверхностной плотностью в точке А, отстоящей на расстояния r от оси цилиндра. Из соображений симметрии следует, что напряженность в любой точке направлена вдоль радиальной прямой, перпендикулярной к оси цилиндра, а значение напряженности зависит лишь от расстояния r от цилиндра. Вырежем из бесконечно длинного цилиндра элемент длиной h. Окружим этот элемент цилиндрической поверхностью (коаксиальной с заряженной) радиуса r, так, чтобы эта поверхность проходила через точку А (рис. 2.15). Для оснований внешнего цилиндра , для боковой поверхности (заряд считаем положительным) . Силовые линии поля пересекают только боковую поверхность цилиндра радиуса r. Следовательно, поток вектора через эту замкнутую поверхность будет равен . Если внутрь поверхности попадает заряд , где –поверхностная плотность заряда. Применяя теорему Гаусса, получаем: , , откуда . (5) Если , рассматриваемая замкнутая поверхность не содержит внутри зарядов, вследствие чего . Таким образом, внутри заряженной цилиндрической поверхности поле отсутствует. Если радиус цилиндра , а заряд распределяется по длине цилиндра с линейной плотностью τ. Тогда можно формулу (17) преобразовать: Тогда (6)

2. 1) Поле вблизи поверхности проводника: E = пов.плотность/E0

Доказательство:

Ф = Qin/E0

Фосн.внешн. + Фосн.внутр. +Фбок. = пов.плотность *Sосн./E0

E*Sосн. + 0*Sосн. +0 = пов.плотность *Sосн./E0

E = сигма/E0

2)Максимальная поверхностная плотность заряда достигается в местах самой большой кривизны

Док-во: хардкор. Примеры: громоотвод, свечение мачт («Огни Эльма»)

3. 

4. Потенциал заряженной плоскости

Поле плоскости ортогонально к ней. Если это направление взять за ось x, то

Здесь

Из соотношения

получаем для потенциала заряженной плоскости

(1.41)

где (0)  произвольная постоянная интегрирования (потенциал плоскости).

5. Потенциальная энергия системы точечных зарядов. В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Q_i (i = 1, 2, ... , n). Энергия взаимодействия всех n зарядов определится соотношением

,

где r_ij - расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.

6. Ёмкость сферического конденсатора:

Два проводника, имеющие форму концентрических сфер с радиусами R₁ и R₂ (R₂ > R₁), образуют сферический конденсатор. Используя теорему Гаусса, легко показать, что электрическое поле существует только в пространстве между сферами. Напряженность этого поля

,

где q - электрический заряд внутренней сферы; - относительная диэлектрическая проницаемость среды, заполняющей пространство между обкладками; r - расстояние от центра сфер, причем R₁ r R₂. Разность потенциалов между обкладками

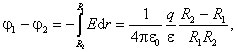
и емкость сферического конденсатора

7. 

8. 

9. Ну тут всё понятно.

10. 

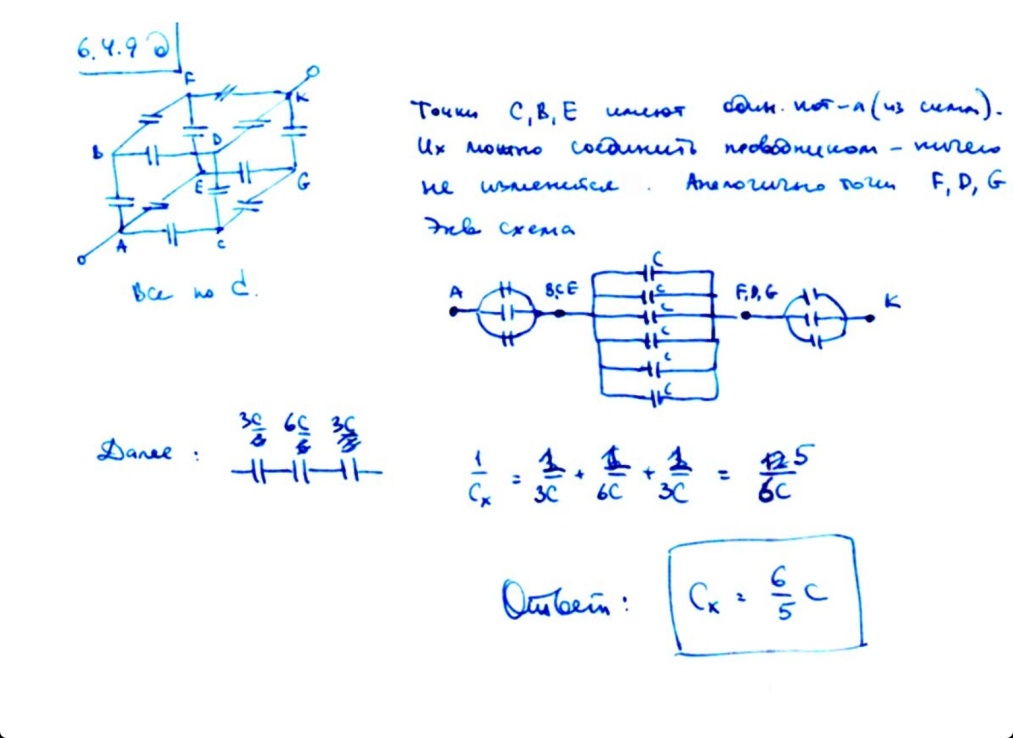
На «5»