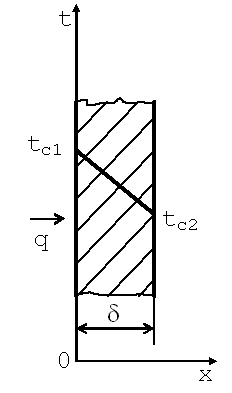
Теплопроводность через плоскую стенку

Рис. 9.2. Однородная плоская стенка

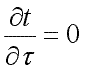Рассмотрим однородную плоскую стенку толщиной δ (рис. 9.2). На наружных поверхностях стенки поддерживаются постоянные температуры t_с1 и t_с2. Коэффициент теплопроводности стенки постоянен и равен λ. При стационарном режиме ( ) и отсутствии внутренних источников теплоты (q_v=0) дифференциальное уравнение теплопроводности примет вид:

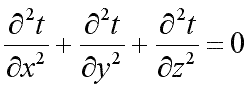(9.16)

При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки (ось Оx). В этом случае

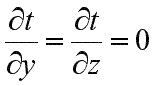
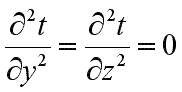
и дифференциальное уравнение теплопроводности перепишется в виде:

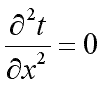(9.17) Граничные условия первого рода запишутся следующим образом: при x=0 t=t_c1; при x=δ t=t_c2. Интегрируя уравнение (9.17), находим

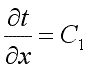
После второго интегрирования получаем

(9.18)

Постоянные С₁ и С₂ определим из граничных условий: при x=0 t=t_c1, С₂=t_c1; при x=δ t=t_c2=С₁·δ+t_c1, отсюда 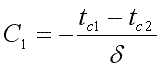 . Подставляя значения С₁ и С₂ в уравнение (9.18), получим уравнение распределения температуры по толщине стенки:

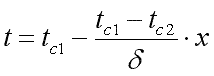(9.19)

Для определения плотности теплового потока, проходящего через стенку в направлении оси Оx, воспользуемся законом Фурье, согласно которому  .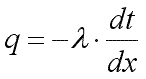

Учитывая, что 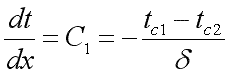 , получим

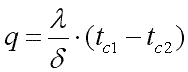.(9.20) Общее количество теплоты, которое передается через поверхность стенки F за время τ,

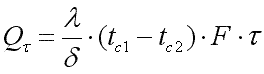(9.21) Отношение   называют тепловой проводимостью стенки, обратную ей величину 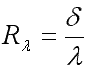  - термическим сопротивлением теплопроводности. Поскольку величина λ зависит от температуры, в уравнения (9.20), (9.21) необходимо подставить коэффициент теплопроводности λ_с, взятый при средней температуре стенки.

Передача теплоты теплопроводностью связана с наличием разности температур тела. Совокупность значений температур всех точек тела в данный момент времени называется температурным полем. В общем случае уравнение температурного поля имеет вид:

(9.1) где t — температура тела; х, у, z — координаты точки; τ — время. Такое температурное поле называется нестационарным и отвечает неустановившемуся режиму теплопроводности. Если температура тела не изменяется с течением времени, то температурное поле называется стационарным. Тогда

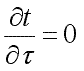(9.2)

Температура может быть функцией одной, двух и трех координат, соответственно температурное поле будет одно-, дву- и трехмерным. Наиболее простой вид имеет уравнение одномерного стационарного температурного поля:

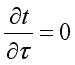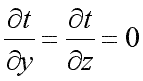; ; . Если соединить все точки тела с одинаковой температурой, то получим поверхность равных температур, называемую изотермической. Так как в определенной точке тела в данный момент времени может быть только одна температура, изотермические поверхности не пересекаются; все они либо замыкаются на себя, либо заканчиваются на границе тела. Пересечение изотермных поверхностей плоскостью дает на ней семейство изотерм. Интенсивность изменения температуры в каком-либо направлении характеризуется производной  , принимающей наибольшее значение в направлении нормали к изотермической поверхности

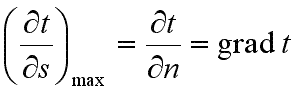(9.3) Вектор   называется температурным градиентом и является мерой интенсивности изменения температуры в направлении по нормали к изотермной поверхности. Направлен он в сторону возрастания температуры.