
- •2.2. Энергетическая форма записи закона Фурье. Коэффициент температуропроводности
- •2.3. Дифференциальное уравнение теплопроводности (дифференциальное уравнение Фурье)
- •8. Понятие о конвективном массообмене и основных теплофизических свойствах к описанию процесса переноса массы Понятие об основных и производных системных единиц измерения в массообмене.
- •Основные механизмы передачи тепла
- •Теплопроводность
- •15 Условия однозначности и расчет задач тепломассопереноса. Граничные условия 1,2,3,4 рода. Условия Стефана
- •16 Понятие о задачи теплопроводности в твердой стенке. Уравнение к определению поля температуры.
- •Теплопроводность через плоскую стенку
- •17 Понятие о методе анализа размерности, отличие его от метод подобия
- •18 Три основные теоремы к исследованию процесса тепломассообмена
- •Закон теплопроводности Фурье
- •Закон Ньютона-Рихмана (основной закон теплоотдачи)
- •19 Метод масштабных преобразований к сведению системы в безразмерному виду. (в чем он состоит)
- •23. Понятие о критериях гидродинамического типа в ршении задач теплообмена: критерий гомохромности, струхаля, жуковского, рейнольдса, эйлера, фруда.
- •24. Понятие о критериях теплового подобия. Нестационарная задача: критерий гомохромности фурье
- •25.Конвективный тепломассообмен и критерии подобия его описания: нусельт, шервуд, пекле, рейнольдс, прандтль, шмит, льюис-семенова, остроградский, экердт, мах
- •26. Основные критерии в описании условий однозначности- критерий Био, Кирпичева. Сходства и различия с критерием нуссельта
- •32. Структура течения в круглой цилиндрической трубе и универсальные законы распределения поля скорости и температуры в области гидродинамической стабилизации
- •33. Понятие о турбулентных потоках теплоты и массы в рамках статистического метода
Основные механизмы передачи тепла
Теплопроводность
Теплопроводность – диффузионный ( кондуктивный) перенос теплоты за счет взаимодействия атомов в узлах их решеток; перенос энергии свободными электронами.
Конвективный перенос (конвекция)
Конвекция – перенос энергии вместе с движущимися макрообъемами теплоносителя.
Конвекция существует в жидкостях и газах.Конвекция всегда сопровождается теплопроводностью.
Тепловое излучение
Тепловое излучение – электромагнитное излучение в инфракрасном диапазоне длин волн.
Любой реальный теплообмен представляет собой конкретную комбинацию этих трех механизмов.
12 Уравнение теплового баланса Согласно закону сохранения энергии в замкнутой системе при теплообменеколичество теплоты, отдаваемое более нагретыми телами, равно получаемой болеехолодными. Считая полученное телом количество теплоты положительным (ΔQ>0), аотданное – отрицательным (ΔQ<0), алгебраическая (с учетом знаков)сумма теплоты, отданной и полученной всеми телами, равна нулю: ΔQ1+ΔQ2+…ΔQn=0.
Вну́тренняя эне́ргия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:
![]()
где
![]() —
подведённое
к телу количество теплоты, измеренное
в джоулях
—
подведённое
к телу количество теплоты, измеренное
в джоулях
![]() [1] — работа,
совершаемая телом против внешних сил,
измеренная в джоулях
[1] — работа,
совершаемая телом против внешних сил,
измеренная в джоулях
Эта формула является математическим выражением первого начала термодинамики
Средняя кинетическая энергия молекул идеального газа (Eк). Пример см. здесь.
Содержание |
Величина |
Наименование |
С |
Eк - средняя кинетическая энергия молекул газа |
Дж |
v - средняя скорость движения молекул |
м/с |
|
n - концентрация молекул |
1/м3 |
|
m0 - масса молекулы |
кг |
|
p - давление |
Па = Н/м2 |
|
i - число степеней свободы, для одноатомного газа i = 3 |
- |
|
T - абсолютная температура газа (to + 273) |
К |
|
k = 1,38 . 10-23 |
Дж/К |
13 Уравнение баланса энтропии
В термодинамике неравновесных процессов принимается, что энтропия S (локальная энтропия) элементарного объема является функцией от внутренней энергии U, удельного объёма V = 1/ и концентрации Сk, и, следовательно, для неё справедливы обычные термодинамические равенства. Эти положения вместе с законами сохранения массы, импульса и энергии позволяют найти уравнение баланса энтропии:
(dS/dt) = - div Js + ,
где: - локальное производство энтропии на единицу объёма в единицу времени;
Js – плотность потока энтропии;
div – дивергенция потока энтропии (число характеризующее расхождение векторов, т.е. изменение векторного потока в каждой точке векторного поля)
Энтропия, в отличие от массы, энергии и импульса, не сохраняется, а возрастает со временем в элементе объёма вследствие необратимых процессов (согласно второму началу термодинамики). Кроме того, энтропия может изменяться вследствие втекания её в элемент объёма или вытекания из него, что не связано с необратимыми процессами. Положительность производства энтропии ( 0) выражает в термодинамике необратимых процессов закон её возрастания, составляющий суть второго начала термодинамики.
14.Понятие об изотермической и неизотермической диффузии. Роль скрещивающих эффектов в неизотермическом случае. Механизмы бародиффузии, динодиффузии, концентрационной диффузии
Главной характеристикой диффузии служит плотность диффузионного потока J - количество вещества, переносимого в единицу времени через единицу площади поверхности, перпендикулярной направлению переноса. Если в среде, где отсутствуют градиенты температуры, давления, электрического потенциала и др., имеется градиент концентрации с(х, t), характеризующий ее изменение на единицу длины в направлении х (одномерный случай) в момент времени t, то в изотропной покоящейся среде
J = -D(dс/dх),
где D - коэффициент диффузии (м2/с); знак "минус" указывает на направление потока от больших концентраций к меньшим. Пространственно-временное распределение концентрации:
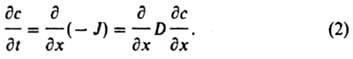
В случае диффузии в многокомпонентных смесях в отсутствие градиентов давления и температуры (изобарно-изотермическая диффузия) для упрощения описания взаимного проникновения компонентов при наличии градиентов их концентраций вводят так называемые коэффициенты взаимной диффузии. Например, при одномерной диффузии в двухкомпонентной системе выражение для диффузионного потока одного из компонентов принимает вид:
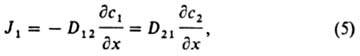
где c1 + с2 = const, D12 = D21 - коэффициент взаимной диффузии обоих компонентов.
В результате неравномерного нагревания среды под влиянием градиента температуры происходит перенос компонентов газовых или жидких смесей - термодиффузия (в растворах - эффект Соре). Если между отдельными частями системы поддерживается постоянная разность температур, то вследствие термодиффузии в объеме смеси появляются градиенты концентрации компонентов, что инициирует обычную диффузию.
Характерным примером процесса переноса, в котором учитывается взаимное влияние двух потоков, диффундирующего вещества и тепла, служит неизотермическая диффузия (или термодиффузия). Это перенос компонент газовой смеси или растворов при наличии в них градиента темп-ры. Если разность темп-р поддерживается постоянной, то вследствие Т. в объёме смеси возникает градиент концентрации, что вызывает и обычную диффузию. В стационарных условиях при отсутствии потока вещества Т. уравновешивается обычной диффузией и в объёме возникает разность концентраций, которая может быть использована, напр., для разделения изотопов. Т. в растворах наз. эффектом Соре - по имени швейц. химика Ш. Соре (Ch. Soret), впервые в 1879-81 исследовавшего Т.
В бинарной смеси при пост. давлении и отсутствии внеш. сил полный диффуз. поток вещества равен
где D12- коэф. диффузии, Dt - коэф. Т., n - число частиц смеси в единице объёма, ci= ni/n - концентрация частиц i -го компонента (i=1, 2). Распределение концентрации в стационарном состоянии может быть найдено из условия ji = 0, откуда
где k т =D т/D12- термодиффузии отношение, пропорционально произведению концентраций компонент.
Коэф. Т. сильно зависит от межмолекулярного взаимодействия, поэтому его изучение позволяет исследовать силы межмолекулярного взаимодействия в газах.
Процесс, обратный Термодиффузии, наз. Дюфура эффектом.
Концентрационная диффузия. Закон Фика: в однородной по температуре и давлению макроскопически неподвижной двухкомпонентной смеси плотность потока массы одного из компонентов за счет молекулярной диффузии пропорциональна градиенту концентрации:
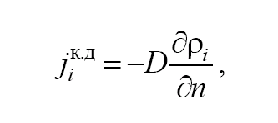
где D – коэффициент молекулярной диффузии одного компонента относительно другого; n – направление нормали к поверхности одинаковой концентрации данного вещества. Диффузия, описываемая законом Фика, называется концентрационной диффузией. Из кинетической теории газов следует, что коэффициент диффузии D возрастает с ростом температуры и уменьшением давления. Кроме того, он зависит от пропорций смеси (чем больше концентрация, тем больше зависимость), однако в технических расчетах ею пренебрегают.
Бародиффузия возникает за счет градиента полного давления. Тяжелые молекулы стремятся перейти в область повышенного давления, легкие – наоборот. Бародиффузия тоже сопровождается переносом массы из-за разности концентраций:
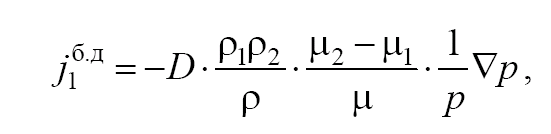
где р – местное давление смеси, равное сумме парциальных давлений компонентов смеси р1 и р2; u1 и u2 – молярные массы компонентов;
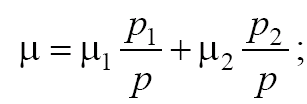 p1,
p2
и p
– плотности компонентов и смеси
соответственно.
p1,
p2
и p
– плотности компонентов и смеси
соответственно.
Бародиффузия проявляется при значительном градиенте давления, что в процессах теплообмена встречается редко, а также отсутствует при равенстве молярных масс компонентов.
Таким образом, суммарный перенос массы какого-либо компонента в
неподвижной среде является следствием (суммированием) концентрацион-
ной диффузии, термодифузии и бародиффузии и называется молекулярной
диффузией:
![]()

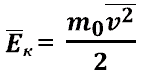 редняя
кинетическая энергия молекул идеального
газа.
Другие формулы, где
встречается средняя энергия молекул
идеального газа:
С
редняя
кинетическая энергия молекул идеального
газа.
Другие формулы, где
встречается средняя энергия молекул
идеального газа:
С редняя
энергия движения молекул и
температура.
О
редняя
энергия движения молекул и
температура.
О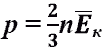 сновное
уравнение МКТ идеального газа
сновное
уравнение МКТ идеального газа