33. Понятие о турбулентных потоках теплоты и массы в рамках статистического метода

При турбулентном течении мгновенная скорость частиц пульсирует около среднего во времени значения. Кроме того, дополнительно к изменению абсолютной величины w происходит еще и изменение направления мгновенной скорости. Отклонение мгновенной скорости w от средней во времени называют пульсациями скорости (пульсационные скорости) , таким образом, турбулентное движение состоит как бы из регулярного течения, описываемого осредненными значениями скоростей, и из наложенного на него хаотического пульсационного течения.

При наличии в потоке температурного поля происходит перенос теплоты, из-за чего возникают пульсации температур. Аналогично обозначению скоростей: . пульсации скорости и температуры приводят к пульсациям давления и физических свойств. Таким образом, турбулентное течение является квазистационарным процессом. Проведя определенное преобразование, выдвинув ряд гипотез, можно получить систему дифференциальных уравнений для осредненного турбулентного течения. Однако в строгой постановке этот вопрос не решен.

Пусть в некоторый момент времени τ + dτ скорость в некоторой точке турбулентного потока имеет свои компоненты . Температура жидкости в данной точке А→ t .

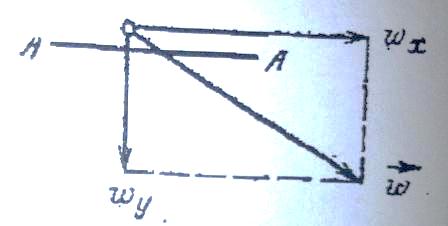
Контрольная поверхность А-А расположена у зафиксированной точки и параллельна плоскости XZ. За время dτ через поверхность А-А проходит масса , . В направлении оси OY проходят относительно оси OX : количество движения и теплота (пусть ρ, - const ). Поскольку компоненты скорости постоянно меняются, среднеинтегральное значение плотности теплового потока в направлении OY :

(1)

Используя свойства среднеинтегрального осреднения, запишем (1) в виде :

(2)

Среднеинтегральное значение количества движения относительно OX, переносимое в направлении OY за единицу времени через единицу поверхности, аналогично (2) запишем как :

(3)

В соответствии с (2) и (3) конвективный перенос складывается из осредненного и пульсационного (турбулентного) переноса.

Обозначим : , (4, 4а)

Знак (-) в (4а) поставлен из-за противоположного направления пульсационного переноса количеству движения.

Поскольку теплота переносится, а количество движения осуществляется на отрезке l, где пульсация существует, то можно записать:

(5)

(6)

Из (5) и (6) следует, что и пропорциональны производным и . Тогда перепишем (5) и (6) в виде:

(7)

(8),

где - коэффициенты турбулентного переноса теплоты и количества движения ; ; – кинематические коэффициенты турбулентного переноса теплоты и количества движения. Размерность соответствуют λ, μ, а, v при молекулярном переносе.

Теплота и количество движения в направлении оси OY переносится одновременно и молекулярным механизмом. Тогда ,

34 Понятие о турбулентных вязкости, теплопроводности и диффузионности, опираясь на турбулентные критерии прандтля, шмита, кинетической энергии турбулентности и скорости диссипации,

Турбулентное течение- процесс сложного поступательно- вращательного вихревого движения молей вещества, в котором при непрерывном движении вихрей и их растяжении за счет деформации имеет место непрервыный спектр пульсации всех тепло-гидрогазодинамически величин и диффузионных величин в интервале длин вол отт мин размеров, кт определяются вязкими силами, до макс размеров, связанных с характерными геом. Особенностями системы, при этом в определенной части спектра пульсации величин , движение носит организованный характер (когерентность) и сопровождается свойствами континуальности, иррегулярности (стохастичности), диффузионности, высокими значениями чисел Re, построенными как по осредненным параметрам, так и по локальным характеристикам вихря ( кин. Энергия вихря, скорость диссипации, время пульсации дин. Поля, псевдозавихренность, интегральный масштаб организованной структуры), диссипитативности.

скорость диссипации ε турбулентной кинетической энергии. Ее физический смысл – скорость, с которой турбулентная кинетическая энергия K превращается в тепло вследствие вязкого трения. Размерность ε = м²/с³

!!! Кинетическая энергия турбулентности скалярная характеристика поля пульсационных величин.

Из уравнения (2.25) переноса напряжений Рейнольдса

Полагаем, что i=j, суммируя по всем i, получаем уравнение энергии

Где

D_t – коэффициент диффузии, Е – кин энергия , L - масштаб турбулентности

µ- Коэф. Дин. Вязкости

******

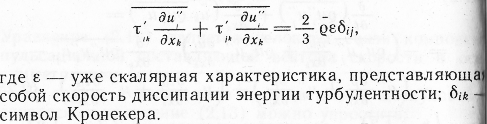
Соответственно турбулентные критерии

Критерий Шмидта является диффузионным критерием (аналогичен критерию Прандтля для теплообмена):

***Прандтль турбулентный и Шмит чаще всего полагают равными 0,9