1. Термодинамическая система – некая физическая система, состоящая из большого количества частиц, способная обмениваться с окружающей средой энергией и веществом.

Открытая ТС – в системе происходят обменные процессы с окружающей средой;

Закрытая термодинамическая система – обмен только энергией, но не веществом;

Изолированная ТС – не обменивается ни энергией ни веществом.

Внутренние и внешние параметры к описанию ТС: P,V,T, U,S,H

2 Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем.

Первое начало термодинамики было сформулировано в середине XIX века в результате работ немецкого учёного Ю. Р. Майера, английского физика Дж. П. Джоуля и немецкого физика Г. Гельмгольца^[1]. Согласно первому началу термодинамики, термодинамическая система может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника.

Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики^[2] (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.

Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю.

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

• «Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии).

Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано.

Второе начало термодинамики в аксиоматической формулировке Рудольфа Юлиуса Клаузиуса (R. J. Clausius, 1865) имеет следующий вид^[2]:

Для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния  , называемая энтропией, такая, что ее полный дифференциал  .

Нулевое начало термодинамики (общее начало термодинамики) — физический принцип, утверждающий, что вне зависимости от начального состояния изолированной системы в конце концов в ней установится термодинамическое равновесие, а также что все части системы при достижении термодинамического равновесия будут иметь одинаковую температуру. Тем самым нулевое начало фактически вводит и определяет понятие температуры. Нулевому началу можно придать чуть более строгую форму:

Если система   находится в термодинамическом равновесии с системой  , а та, в свою очередь, с системой  , то система   находится в равновесии с  . При этом их температуры равны.

Позитивность первого закона термодинамики в том, что энергия не зависит от пути перехода, в то время как любой из параметров существенно зависит. Локальный характер процессов переноса мб описан в рамках неравновесной термодинамики конкретными механизмами определяемыми тепломассобменом.

3 Теплообмен – самопроизвольный необратимый процесс переноса теплоты в пространстве, обусловленный неоднородным полем температуры.

Три основных механизма процесса переноса теплоты:

• Теплопроводность;

• Конвекция;

• Излучение (лучистый теплообмен);

Конвективный теплообмен – процесс обмена энергией между движущейся средой и поверхностью твердого тела, является сочетанием передачи тепла теплопроводностью в твердой стенке и конвекцией в жидкой среде.

Конвективный теплообмен между потоком жидкости или газа и по-

верхностью твердого тела называется конвективной теплоотдачей. Обычно

при инженерных расчетах определяют теплоотдачу, знание конвективного

теплообмена внутри жидкой среды может представить при этом косвенный

интерес, поскольку перенос тепла внутри жидкости отражается и на теплоот-

даче. Результирующий поток тепла всегда направлен в сторону уменьшения

температуры.

При практических расчетах используют закон Ньютона – Рихмана:

Согласно закону Ньютона – Рихмана тепловой поток от жидкости

к стенке или от стенки к жидкости пропорционален поверхности теплообме-

на и разности температур поверхности стенки и окружающей среды (темпе-

ратурному напору).

Функция состояния термодинамической системы – функция, зависящая от нескольких независимых параметров, которые однозначно определяют состояние термодинамической системы. Значение термодинамической функции состояния зависит только от состояния системы, а не от того, как система пришла в это состояние.

4 Существуют различные виды сложного переноса тепла, которые являются сочетанием элементарных видов. Основные из них:

• теплоотдача (конвективный теплообмен между потоками жидкости или газа и поверхностью твёрдого тела);

• теплопередача (теплообмен от горячей жидкости к холодной через разделяющую их стенку);

• конвективно-лучистый перенос тепла (совместный перенос тепла излучением и конвекцией);

В действительных условиях работы различных теплообменных устройств теплота передается одновременно теплопроводностью, конвекцией и излучением. Такое явление называется сложным теплообменом.

Например, в газоходах паровых котлов теплота передается не только излучением, но и конвекцией. В этом случае суммарный тепловой поток

.

(12.1)

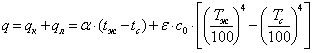
Если в качестве основного процесса теплообмена принято тепловое излучение, то

.

(12.2)

Перенос теплоты конвекцией здесь учитывается увеличением приведенной степени черноты системы за счет

.

(12.3)

В тех случаях, когда конвективная составляющая теплового потока значительно превышает лучистую составляющую, в качестве основного процесса принимается конвекция, и тепловой поток определяется уравнением:

,

(12.4)

где

.

(12.5)

5 Закон Фурье, коэффициент теплопроводности

В 1807 году французский ученый Фурье (Fourier) предложил считать, что в каждой точке тела (вещества) в процессе теплопроводности существует однозначная связь между тепловым потоком и градиентом температуры:

, (*)

где Q – тепловой поток, Вт; grad(T) – градиент температурного поля, К/м; F – площадь поверхности теплообмена, м²; , – коэффициент теплопроводности , – величина, характеризующая физические свойства вещества. Коэффициент теплопроводности определяют экспериментально и приводят в справочной литературе.

Закон Фурье для поверхностной плотности теплового потока запишется в виде

. (**)

Физический смысл коэффициента теплопроводности заключается в том, что он (λ) характеризует способность данного вещества проводить теплоту.

Коэффициент теплопроводности λ находят экспериментально, используя выражения (*) и (**) решением, так называемой, обратной задачи теории теплопроводности.

Знак "–" показывает, что векторы теплового потока и градиента температуры направлены в противоположные стороны. Градиент температурного поля направлен по нормали к изотермической поверхности в сторону возрастания температуры, тепловой поток – в сторону убывания температуры. Выражения (*) и (**) представляют собой линейный закон теплопроводности, т.к. в этом законе коэффициент теплопроводности есть величина постоянная (λ = const). При экспериментальной проверке закона Фурье обнаруживается отклонение расчета и эксперимента, которое в первом приближении можно учесть, сохранив форму записи закона, но приняв зависимость λ = f(T). В этом случае получаем нелинейный закон Фурье:

.

Для разных веществ и их фазового состояния λ может, как увеличиваться, так уменьшаться с ростом температуры. Для пористых и сыпучих материалов коэффициент теплопроводности λ также зависит от порозности (величина пор) и от влажности. С увеличением порозности λ уменьшается, так как поры заполняются газом, а λ газов мал. При увеличении влажности поры заполняются влагой, и коэффициент теплопроводности λ увеличивается. Примеси уменьшают коэффициент теплопроводности. Коэффициент теплопроводности газов также зависит и от давления.

Вещество	λ, Вт/(м·К)
Газы Жидкости	0,005÷0,4 0,08÷0,7

Приведем примерные значения коэффициента λ разных веществ. Поскольку λ функция температуры, то эти данные взяты из справочника при t = 0 ⁰С.

2.2. Энергетическая форма записи закона Фурье. Коэффициент температуропроводности

Коэффициент температуропроводности а, [м²/с] – физическая характеристика вещества, которая определяется экспериментально и приводится в справочных таблицах.

Коэффициент температуропроводности а, характеризует теплоинерционные свойства вещества или другими словами характеризует скорость изменения температуры тела во времени. Скорость изменения температуры ~ а, прямо пропорциональна коэффициенту температуропроводности. Т.о. коэффициент температуропроводности характеризует только нестационарные процессы.

Коэффициент температуропроводности связан с другими физическими характеристиками вещества, следующими соотношениями:

; ,

где с – удельная массовая теплоемкость, Дж/(кг·град); - удельная объемная теплоемкость, Дж/(м³·град); ρ – плотность, кг/м³; λ – коэффициент теплопроводности Вт/(м·град);.

Для твердых тел, обладающим малым коэффициентом температурного расширения .

Для газов, у которых теплоемкость зависит от вида процесса, естественно, и коэффициент температуропроводности является функцией процесса:

— для изохорного процесса v=const: ;

— для изобарного процесса p=const: .

Порядок величины коэффициента температуропроводности можно характеризовать следующими величинами:

а ≈ 10^-7 м²/с – для тепловой изоляции;

а ≈ 10^-6 м²/с – для огнеупоров;

а ≈ 10^-5 м²/с – для стали.

Для представления закона Фурье в энергетической форме заменим λ в классической форме записи закона теплопроводности выражением

или .

Получим

– для изохорных процессов,

где – удельная объемная внутренняя энергия, Дж/м³;

– для изобарных процессов,

где - удельная объемная энтальпия, Дж/м³.

Для твердых тел энергетическая форма записи закона Фурье имеет вид:

2.3. Дифференциальное уравнение теплопроводности (дифференциальное уравнение Фурье)

Если поместить тело, например, бесконечную пластинку толщиной δ и начальной температурой T₀ в горячую среду с температурой T_f (рис. 1.1), то пластинка, получая энергию от горячей среды, будет нагреваться, и ее температура изменяется с течением времени в каждой точке.

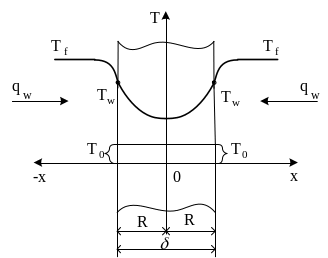
Рис. 2.1. Нагрев пластины в среде с температурой T_f

Температурное поле , т.е. распределение температур в пространстве и во времени, находят решением дифференциального уравнения (ДУ) теплопроводности, которое в 1814 году вывел французский ученый Фурье и поэтому это уравнение носит его имя. Вывод ДУ теплопроводности основан на законе сохранения энергии и использует закон Фурье. Уравнение Фурье моделирует процессы, которые в процессе теплопроводности протекают в каждом элементарном объеме тела:

1) поглощение тепловой энергии при нагреве или выделение при охлаждении;

2) прохождение теплоты через элементарный объем транзитом;

3) выделение или поглощение теплоты за счет действия внутренних источников или стоков теплоты мощностью q_v.

В векторной форме записи дифференциальное уравнение теплопроводности имеет вид:

,

где – удельная объемная теплоемкость, Дж/(м³К); – плотность, кг/м³; с – удельная массовая теплоемкость, Дж/(кгК).

Напомним, что для твёрдых тел .

Решая это уравнение, мы получим температурное поле: Т(х_i, ). Т.о. дифференциальное уравнение теплопроводности устанавливает связь между пространственным и временным изменениями температуры.

Вид формул для операторов дивергенции (div) и градиента (grad) зависят от выбора системы координат. Например, в декартовой системе координат ДУ теплопроводности примет вид:

,

или принимая допущение о независимости физических свойств вещества от температуры { }

,

где – коэффициент температуропроводности, м²/с.

В нашем кратком курсе ТМО будем решать дифференциальное уравнение Фурье для тел простейшей формы (бесконечная пластина, бесконечный цилиндр и шар или сфера) с постоянными физическими коэффициентами:

,

где x₁ – первая координата в ортогональной системе координат: x₁ = x в декартовой системе координат, x₁ = r в цилиндрической и сферической системах координат; k = 1, 2 или 3 – коэффициент формы тела: k = 1 – бесконечная пластина; k = 2 – бесконечный цилиндр; k = 3 – шар.

При отсутствии в системе внутренних источников\стоков теплоты (q_v = 0) дифференциальные уравнения Фурье для тел простейшей формы записываются следующим образом:

k = 1 : ; k = 2 : ;k = 3 : .

При неизменных условиях теплообмена (постоянных температурах флюида, омывающих тело с разных сторон, и постоянных коэффициентах теплоотдачи) на границах тела его температурное поле с некоторого момента времени перестает изменяться во времени и наступает стационарный режим теплопроводности, который для тел простейшей формы описывается уравнением Пуассона при действии внутренних источников теплоты

,

или уравнением Лапласа, если q_v =0

.

В результате решения одномерного дифференциального уравнения для стационарного процесса теплопроводности находят температурное поле в виде T(x₁) или в явном виде T(x) – в декартовой системе координат и T(r) – в цилиндрической и сферической системах координат.

Анизотропи́я— неодинаковость свойств среды (например, физических: упругости, электропроводности,теплопроводности, показателя преломления, скорости звука или света и др.) по различным направлениям внутри этой среды; в противоположность изотропии.

В отношении одних свойств среда может быть изотропна, а в отношении других — анизотропна; степень анизотропии также может различаться.

6 Принцип Кюри и понятие о скрещивающих эффектах между теплотой и массой: термодиффузия, эффект Сорре, диффузионная теплопроводности, эффект Дюфо

принцип Кюри для изотропных систем, свойства которых одинаковы во всех направлениях: потоки и движущие силы разной тензорной размерности не могут быть связаны друг с другом. Так, например, причина-скаляр не может вызвать векторный поток.       Таким образом, согласно принципу Кюри линейные соотношения и принцип симметрии феноменологических коэффициентов справедливы только для потоков и сил одинаковой тензорной размерности. 

     

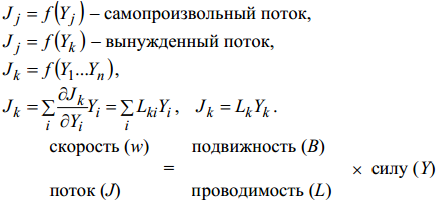
По тензорной размерности необратимые процессы можно разделить на три группы:  1. скалярные - химические реакции, теплообмен и массообмен между фазами;  2. векторные - диффузия и теплопроводность в сплошной фазе, вязкое взаимодействие между фазами;  3. тензорные - вязкое взаимодействие в сплошной фазе. 

ТЕРМОДИФФУЗИЯ

- перенос компонент газовой смеси или растворов при наличии в них градиента темп-ры. Если разность темп-р поддерживается постоянной, то вследствие Т. в объёме смеси возникает градиент концентрации, что вызывает и обычную диффузию. В стационарных условиях при отсутствии потока вещества Т. уравновешивается обычной диффузией и в объёме возникает разность концентраций, к-рая может быть использована, напр., для разделения изотопов. Т. в растворах наз. эффектом Соре - по имени швейц. химика Ш. Соре (Ch. Soret), впервые в 1879-81 исследовавшего Т.

В бинарной смеси при пост. давлении и отсутствии внеш. сил полный диффуз. поток вещества равен 

где D₁₂- коэф. диффузии, D_t - коэф. Т., n - число частиц смеси в единице объёма, c_i= n_i/n - концентрация частиц i -го компонента (i=1, 2). Распределение концентрации в стационарном состоянии может быть найдено из условия j_i = 0, откуда 

где k _т = D _т/D₁₂- термодиффуз. отношение, пропорц. произведению концентраций компонент.

Коэф. Т. сильно зависит от межмолекулярного взаимодействия, поэтому его изучение позволяет исследовать силы межмолекулярного взаимодействия в газах.

Процесс, обратный Т., наз. Дюфура эффектом.

13.7. ЭФФЕКТ ТЕРМОДИФФУЗИИ

В бинарном ламинарном пограничном слое в определенных условиях существенно проявляется термодиффузия. Особенно существен здесь эффект Дюфо, заключающийся в возникновении градиента температуры при адиабатической диффузии.

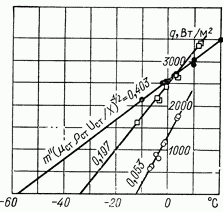
Рис. 13.7. Зависимость теплового потока от разности температур и параметра проницаемости стенки при обтекании лобовой точки пористого тела системой воздух—водород

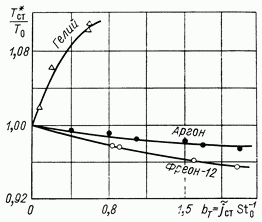
Рис. 13 8. Равновесная температура пористой адиабатической пластины при вдуве инородного газа в турбулентный пограничный слой воздуха

В результате температура поверхности адиабатической пористой пластины может существенно отличаться от температуры вне пограничного слоя. Таким образом, здесь также целесообразно ввести понятие адиабатической температуры стенки, сохранив за этой величиной обычное ее обозначение, и определять тепловой поток, как обычно в таких случаях, по формуле

(13.7.1)

При этом коэффициент теплоотдачи а консервативен относительно эффекта термодиффузии (рис. 13.7).

В турбулентном пограничном слое этот эффект существенно меньше, что видно из данных П. А. Романенко и Ю. П. Семенова, показанных на рис. 13.8.

7 Тепловой поток (обозначают ) – количество теплоты, проходящее через заданную и нормальную к направлению распространения теплоты поверхность в единицу времени:

.

Процесс переноса тепла за счет теплопроводности при отсутствии внутренних источников тепла, когда температура системы изменяется не только от точки к точке, но и с течением времени – называется НЕстационарным.

Для трехмерного температурного поля дифференциальное уравнение теплопроводности по аналогии можно записать в виде (гиперболическое уравнение закона теплопроводности)

Время релаксации — период времени, за который амплитудное значение возмущения в выведенной из равновесия физической системе уменьшается в e раз (e — основание натурального логарифма), в основном обозначается греческой буквой τ.

Согласно принципу Ле Шателье — Брауна при отклонении физической системы от состояния устойчивого равновесия возникают силы, которые пытаются вернуть систему к равновесному состоянию. Если в состоянии равновесия некоторая физическая величина f имеет значение , причём отклонение от равновесия , то в первом приближении можно считать, что эти силы пропорциональны отклонению. Кинетическое уравнение для величины f запишется в виде

где λ — некоторый параметр, а знак минус указывает на то, что реакция системы на возмущение приводит к возвращению к равновесному состоянию.

Время релаксации: В таком случае величина f будет изменяться по закону:

где  - - начальное возмущение.
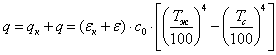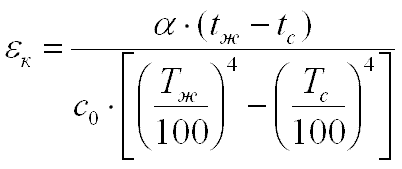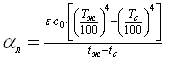