Завдання № 1.26

Сумісна система лінійних неоднорідних рівнянь має єдиний розв’язок, якщо:

1. Ранг основної матриці дорівнює рангу розширеної матриці і бі­льший від кількості невідомих;

2. Ранг основної матриці дорівнює рангу розширеної матриці і менший від кількості невідомих;

3. Ранг основної матриці дорівнює рангу розширеної матриці і менший від кількості рівнянь;

4. Ранг основної матриці дорівнює рангу розширеної матриці і до­рівнює кількості невідомих:

5. Ранг основної матриці дорівнює рангу розширеної матриці і рі­вний кількості рівнянь.

4.2. Класична регресія в економетриці Завдання № 2.1

В економетриці незалежну змінну називають:

1. Ендогенна змінна;

2. Показник;

3. Пояснювана змінна;

4. Регресор;

5. Результат.

Завдання № 2.2

В економетриці залежну змінну називають:

1. Екзогенна змінна;

2. Параметр;

3. Пояснювальна змінна;

4. Регресанд:

5. Фактор.

Завдання № 2.3

Залежність між незалежними змінними ..., і залежною змінною називають стохастичною, якщо:

1. Кожному впорядкованому набору значень незалежних змінних ставиться у відповідність одне значення залежної змінної;

2. Кожному впорядкованому набору значень незалежних змінних ставиться у відповідність декілька значень залежної змінної;

3. Кожному впорядкованому набору значень незалежних змінних ставиться у відповідність середнє значення залежної змінної;

4. Якщо між змінними є явище автокореляції;

5. Якщо між змінними наявна мультиколінеарність.

Завдання № 2.4

Залежність між незалежними змінними ..., і залежною змінною називають кореляційною, якщо:

1. Кожному впорядкованому набору значень незалежних змінних ставиться у відповідність одне значення залежної змінної;

2. Кожному впорядкованому набору значень незалежних змінних ставиться у відповідність декілька значень залежної змінної;

3. Кожному впорядкованому набору значень незалежних змінних ставиться у відповідність середнє значення залежної змінної;

4. Якщо між змінними існує автокореляція;

5. Якщо між незалежними змінними існує мультиколінеарність.

Завдання № 2.5

Залежність між незалежними змінними ..., і залежною змінною називають функціональною, якщо:

1. Кожному впорядкованому набору значень незалежних змінних ставиться у відповідність одне значення залежної змінної;

2. Кожному впорядкованому набору значень незалежних змінних ставиться у відповідність декілька значень залежної змінної;

3. Кожному впорядкованому набору значень незалежних змінних ставиться у відповідність середнє значення залежної змінної;

4. Якщо між змінними існує автокореляція;

5. Якщо між незалежними змінними існує мультиколінеарність.

Завдання № 2.6

Випадкову величину називають неперервною, якщо:

1. Вона набуває лише додатних значень;

2. Вона розподілена за нормальним законом;

3. Її дисперсія є сталою величиною;

4. Її значення можна занумерувати;

5. Її значення повністю заповнюють деякий числовий проміжок.

Завдання № 2.7

Випадкову величину називають дискретною, якщо:

1. Вона набуває лише додатних значень;

2. Її дисперсія є сталою величиною;

3. Її значення можна занумерувати;

4. Її значення повністю заповнюють деякий числовий проміжок;

5. Її математичне сподівання дорівнює середньому арифметич­ному.

Завдання № 2.8

Діаграмою розподілу є:

1. Графік значень незалежної і залежної змінних;

2. Інша назва множинної регресії;

3. Інша назва простої регресії;

4. Лінія з нахилом і перетином ;

5. Лінія, що відображає зв’язок між незалежною і залежною змін­ними.

Завдання № 2.9

Лінійною регресією є:

1. Графік значень незалежної та залежної змінних;

2. Інша назва простої регресії;

3. Лінія, що відображає зв'язок між незалежною і залежною змін­ною;

4. Лінія, що завжди має нахил, який дорівнює 0;

5. Лінія, що завжди має нахил, що дорівнює 1.

Завдання № 2.10

Нахил у рівнянні парної лінійної регресії:

1. Вимірює зв’язок між залежною і незалежною змінними;

2. Вимірює придатність лінії регресії;

3. Завжди дорівнює 1;

4. Інша назва коефіцієнта детермінації;

5. Це точка, де лінія регресії перетинає вісь .

Завдання № 2.11

Якщо нахил у рівнянні парної лінійної регресії значимо відрізняється від нуля, то це означає, що:

1. Залежна змінна відіграє важливу роль у поясненні незалежної змінної;

2. Залежна змінна не відіграє важливої ролі у поясненні незалеж­ної змінної;

3. Незалежна змінна відіграє важливу роль у поясненні залежної змінної;

4. Незалежна змінна не відіграє важливої ролі у поясненні залеж­ної змінної;

5. Усі відповіді хибні.

Завдання № 2.12

При перевірці значущості нахилу в рівнянні парної лінійної регресії нульова гіпотеза має вигляд:

1.

2.

3.

4.

5.

Завдання № 2.13

Перетин у рівнянні парної лінійної регресії:

1. Вимірює зв'язок між залежною і незалежною змінними;

2. Вимірює придатність лінії регресії;

3. Завжди дорівнює 0;

4. Завжди дорівнює 1;

5. Це точка, в якій лінія регресії перетинає вісь .

Завдання № 2.14

Коефіцієнт детермінації:

1. Вимірює зв’язок між залежною і незалежною змінними;

2. Вимірює придатність лінії регресії;

3. Завжди дорівнює 1;

4. Інша назва коефіцієнта кореляції;

5. Це точка, де лінія регресії перетинає вісь .

Завдання № 2.15

Коефіцієнт детермінації вимірює:

1. Варіацію незалежної змінної;

2. Завжди дорівнює 1;

3. Загальну варіацію залежної змінної, що пояснює регресію;

4. Нахил лінії в моделі парної лінійної регресії;

5. Перетин лінії в моделі парної лінійної регресії.

Завдання № 2.16

Вважають, що між величинами та існує щільний зв'язок, якщо ко­ефіцієнт кореляції міститься на проміжку:

1. (–0,9; –0,7).

2. (–0,6; –0,4);

3. (0,2; 0,4);

4. (0,4; 0,6);

5. (0,5; 0,7).

Завдання № 2.17

Вважають, що між величинами та існує слабкий зв'язок, якщо кое­фіцієнт кореляції міститься на проміжку:

1. (–0,9; –0,7).

2. (–0,6; –0,4);

3. (0,2; 0,4);

4. (0,4; 0,6);

5. (0,5; 0,7).

Завдання № 2.18

Стандартна помилка оцінювання (корінь із середнього квадрату залишків):

1. Вимірює зв’язок між залежною і незалежною змінною;

2. Вимірює придатність лінії регресії;

3. Завжди дорівнює 1;

4. Інша назва коефіцієнта детермінації;

5. Це точка, де лінія регресії перетинає вісь .

Завдання № 2.19

(загальна сума квадратів відхилень) дорівнює:

1.  ;

2.  ;

3.  ;

4.  ;

5.  .

Завдання № 2.20

(сума квадратів відхилень, що пояснює регресію) дорівнює:

1.  ;

2.  ;

3.  ;

4.  ;

5.  .

Завдання № 2.21

(непояснювана сума квадратів відхилень) дорівнює:

1.  ;

2.  ;

3.  ;

4.  ;

5.  .

Завдання № 2.22

Коефіцієнт детермінації обчислюють за формулою:

1. ;

2. ;

3. ;

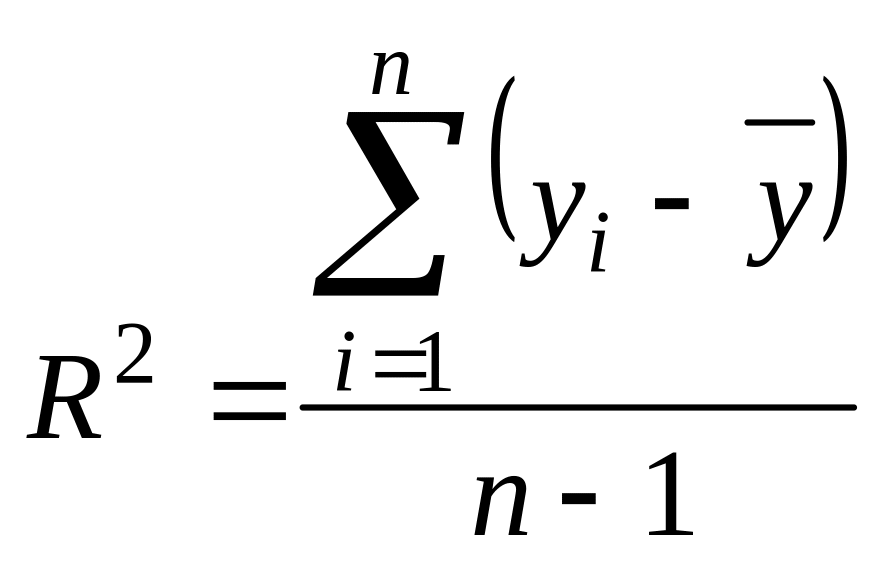4. ;

5. .

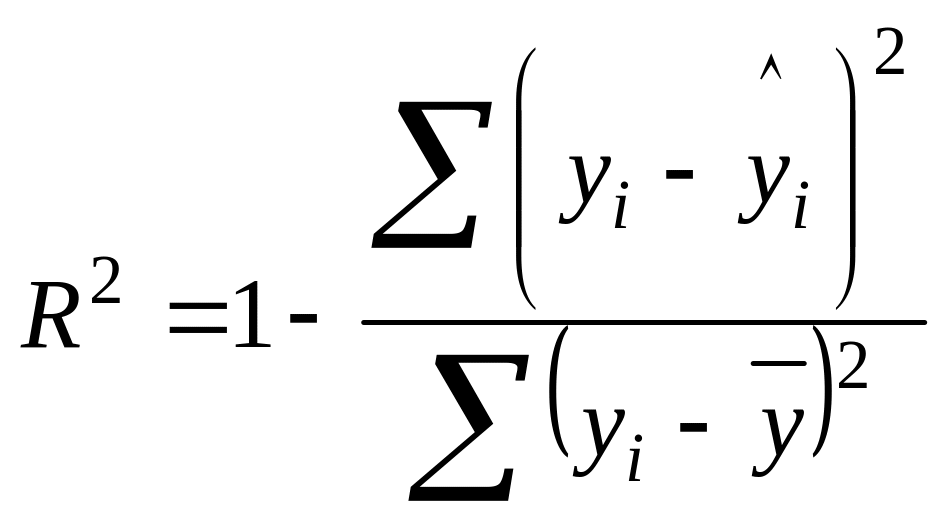Завдання № 2.23

Загальну дисперсію показника обчислюють за формулою:

1. ;

2. ;

3. ;

4. ;

5. .

Завдання № 2.24

Залишкову дисперсію обчислюють за формулою:

1. ;

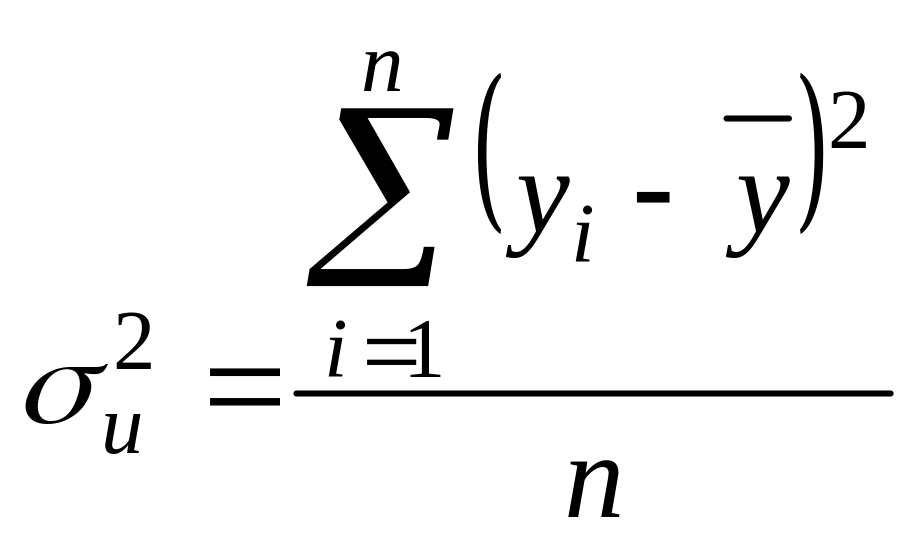2. ;

3. ;

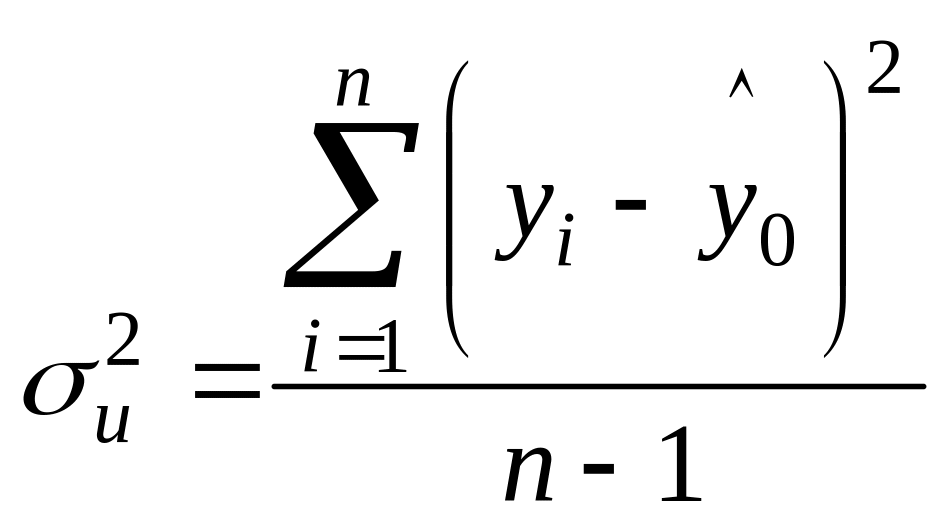4. ;

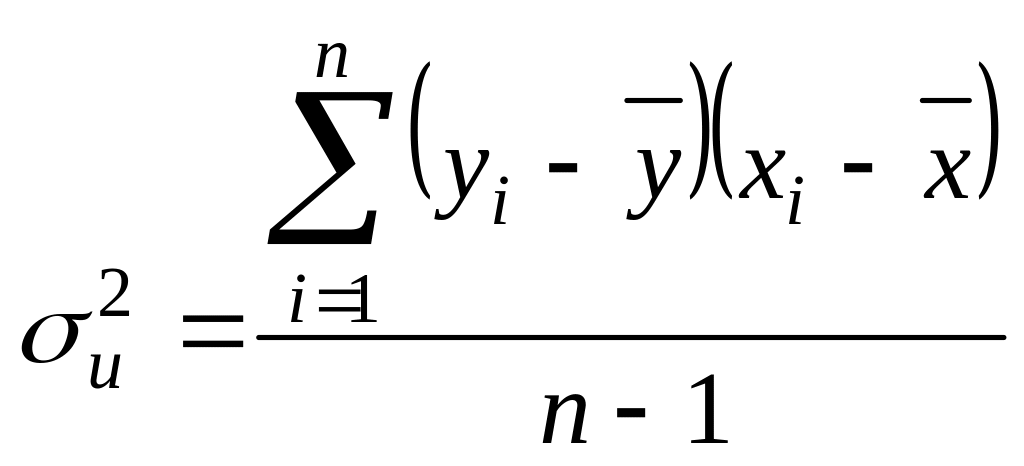5. .

Завдання № 2.25

Коефіцієнт детермінації вимірює:

1. Значущысть коефіцієнтів регресії;

2. Загальну варіацію показника;

3. Загальну варіацію чинника;

4. Частку варіації показника, що пояснюється рівнянням регресії.

Завдання № 2.26

Параметр рівняння множинної лінійної регресії характеризує:

1. Вплив чинника на показник за умови постійності значень інших чинників;

2. Сумарний вплив чинників на показник;

3. Щільність зв'язку між чинником і показником;

4. Сумарний коефіцієнт еластичності.

Завдання № 2.27

Із двох моделей, що описують функціонування однієї економіч­ної сис­теми й адекватні за критерієм Фішера, перевагу слід надавати тій, у якої:

1. Більше числове значення критерію Фішера;

2. Коефіцієнт кореляції додатний;

3. Більше значення коефіцієнта кореляції;

4. Коефіцієнт кореляції від' ємний.

Завдання № 2.28

Для тестування значимості коефіцієнтів рівняння регресії використо­вують:

1. Тест Стьюдента;

2. Тест Фішера;

3. Критерій Пірсона;

4. Критерій Спірмена.