6. Преобразования, как изменение систем координат.

Рассмотренное преобразование множества точек, принадлежащих объекту, в некоторое другое множество точек производилось в одной и той же системе координат. Таким образом, система координат остается неизменной, а сам объект преобразуется относительно начала координат до получения желаемого результата.

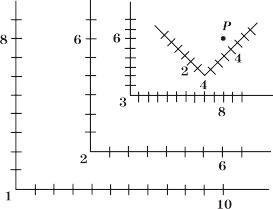
Другим способом описания преобразования является смена систем координат. Такой подход оказывается полезным, когда желательно собрать вместе много объектов, каждый из которых описан в своей собственной локальной системе координат (ЛСК), и выразить их координаты в одной глобальной (ГСК).

Вначале рассмотрим, как положение точки, заданной в одной СК, можно описать в любой другой СК.

Точка имеет координаты:

1 СК — ;

2 СК — ;

3 СК — ;

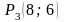4 СК — .

Преобразования СК имеет вид:

1 СК — 2 СК: ;

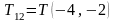2 СК — 3 СК: ;

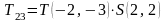3 СК — 4 СК: .

Тогда координаты точки во 2 СК через 1 СК:

.

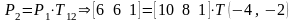Обратное преобразование из 2 СК в 1 СК:

.

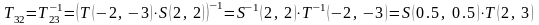Причем:

.

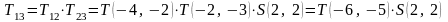7. Устранение искажений в растровых изображениях. Выравнивание. Мелкие и движущиеся объекты. Алгоритм By.

Пусть задан отрезок ненулевой толщины. Какие 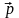высветить? Те, которые более чем на половину покрыты отрезком. Результат на рисунке

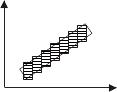
Лестничный эффект

Избавится от него помогает принцип выравнивания: каждый высвечивается с яркостью, пропорциональной площади , занимаемой отрезком. Но использование этого принципа замедляет процесс разложения в растр, т.к. требуются дополнительные алгоритмы.

Другой путь: разрешение экрана. При разрешающей способности экрана в 2 раза по осям X иY общее число в 4 раза, а скорость разложения в растр – в 2 раза.

Р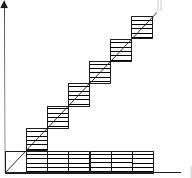 ассмотрим 2 отрезка – горизонтальный и под углом 45⁰.

Яркость отрезков I и II не одинаковая, хотя в их отрисовке участвуют по семь .

Отрезок I имеет максимальную яркость, а отрезок II – минимальную. Следовательно, яркость отрезков зависит от их угла наклона. Чтобы сделать яркость отрезков одинаковой, надо менять интенсивность . Так яркость в отрезке II=1, яркость в отрезке I= .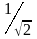

Сглаживание линий

Есть итальянская поговорка: “Необязательно говорить правду, главное, чтобы то, что вы скажите, хорошо звучало”. Это относится и к сглаживанию линий; не нужно рисовать картинку идеально. Нужно, чтобы картинка лишь выглядела как настоящая. Не следует углубляться в сложную математику, чтобы получить идеально сглаженные линии, зрительная система человека видит то, что хочет видеть, так почему бы не дать ей лишь ключ к распознаванию?

Алгоритм Ву

Идея: при рисовании линий обычным образом с каждым шагом по основной оси высвечивается два по неосновной оси.

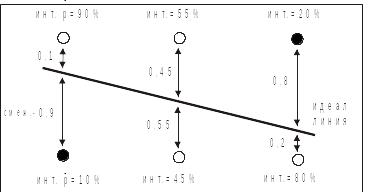
Их интенсивность подбирается пропорционально расстоянию от центра до идеальной линии. Чем дальше т., тем < ее интенсивность. Значение интенсивности 2-ух дают в сумме 1, т.е. это интенсивность 1 , в точности попавшего на идеальную линию. Это придает линии одинаковую интенсивность на всем ее протяжении, создавая иллюзию, что точки расположены вдоль линии не по 2, а по одной в точности по идеальной линии.

Горизонтальные, вертикальные и диагональные линии не требуют сглаживания. Для других линий алгоритм Ву проходит их вдоль основной оси, подбирая координаты по неосновной оси. Смещение вдоль неосновной оси вычисляется 1 целочисленным делением (для линий с наклоном < 1 берется сам наклон, с наклоном > 1 – 1\2 наклона). Это значение называется ошибкой смещения. Ошибка накопления (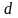 ) показывает, как далеко ушли 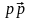от идеальной линии по неосновной оси, и как только она достигает критического значения, делается шаг на 1 вдоль неосновной оси. Если основной осью является X, то будут установлены 2 т. с координатами (x,y) и (x,y+1). Короче говоря, продвижение вдоль линии аналогично алгоритму Брезенхэма, только на каждом этапе устанавливается не 1 , а 2. Осталось определить их интенсивность. Ошибка смещения суммируется с ошибкой накопления.

Пусть число уровней интенсивности кратно 2,

- min интенсивность — ,

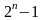- max интенсивность — 0.

С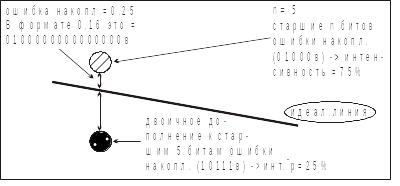 таршие n битов ошибки накопления покажут необходимую интенсивность для одного из . Интенсивность 2-го пары 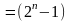- интенсивность 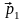. Ошибка накопления содержит соотношение расстояний от центра каждого из двух до идеальной линии.