
- •Основные сведения о графических системах (гс). Функции гс. Блок-схема гс. Основные сведения о графических системах (гс).
- •Функции гс
- •Блок-схема гс.
- •Векторный и растровый дисплеи. Получение изображения. Сравнительная характеристика.
- •Геометрические преобразования. Однородные координаты. Перенос, поворот, масштабирование в однородных координатах. Двумерные преобразования Перенос
- •Масштабирование
- •Поворот
- •Однородные координаты
- •Перенос
- •Композиции преобразований
- •(Трехмерных)
- •Преобразование отрезков в растровую форму. Простой, пошаговый алгоритмы, алгоритм Брезенхема.
- •Преобразования, как изменение систем координат.
- •Устранение искажений в растровых изображениях. Выравнивание. Мелкие и движущиеся объекты. Алгоритм By.
- •Заполнение области. Алгоритм построчного сканирования, алгоритм заполнения с затравкой. Заполнение линиями.
- •Растровая развёртка многоуг-в (метод использования когерентности сканируемых строк).
- •Растровая развёртка многоуг-в (метод использования когерентности рёбер).
- •Алгоритм отсечения отрезков Козна и Сазерленда. Алгоритм разбиения средней точкой.
- •Основные виды геометрических моделей.
- •Методы построения геометрических моделей (построение кривых и поверхностей, кусочно-аналитическое описание, кинематический принцип, булевы операции, полигональные сетки).
- •Поперечное сечение криволинейного объекта и его полигональная аппроксимация
- •Методы создания реалистических трехмерных изображений.
- •Получение проекций. Основные виды проекций.
- •Общие сведения об удалении скрытых линий. Сравнительная характеристика алгоритмов.
- •Алгоритм сортировки по глубине
- •Алгоритм разбиения области
- •Алгоритм, использующий z-буфер
- •Алгоритм построчного сканирования (пи)
- •Методы закраски полигональной сетки.
- •Фактура. Нанесение узора на поверхность
- •Фактура. Создание неровностей на поверхности.
- •Математическое описание перспективных проекций.
- •Алгоритм трассировки лучей.
- •Общие сведения о свете. Классификация поверхностей по виду отражения.
- •Модель освещения. Свойства объектов
- •4 Типа поверхностей:
- •Отражение диффузное
- •Зеркальное отражение
- •Пропускание света (прозрачность)
- •С рассеянным, диффузным и зеркальным с рассеянным и диффузным с рассеянным светом Без освещения
- •Специальные модели
- •Получение теней.
- •Источник на бесконечности
- •Локальный источник
- •Цвет и его характеристики.
- •Цветовые модели(rgb, cмy).
- •Системы смешивания основных цветов
- •Цветовые модели (hsv, hls). Цветовая гармония.
Перенос
Уравнение переноса (1) запишется в виде матрицы преобразования:
 (10)
или
(10)
или
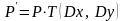 (11)
(11)
где
 ,
,
перемножив, получим:
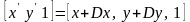 .
.
Докажем, что если
точку
 перенести в
на расстояние
перенести в
на расстояние
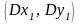 ,
а затем в точку
,
а затем в точку
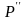 на расстояние
на расстояние
 ,
то в результате получим перенос на
расстояние
,
то в результате получим перенос на
расстояние
 .
.
|
|
 (12)
и (13)
(12)
и (13)
Теперь подставим (12) в (13):
 .
.
Матричное произведение
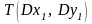 и
и
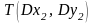 :
:
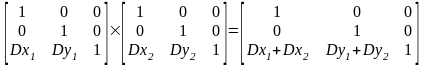
то есть перенос — функция аддитивная.
Масштабирование
Уравнение масштабирования (4) в матричной форме имеет вид:
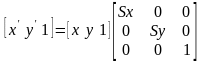 (14)
(14)
Определяя
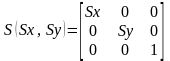 ,
,
имеем
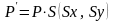 (15)
(15)
перемножив, получим:
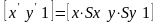 .
.
Поворот
Уравнение поворота (3) можно представить в виде:
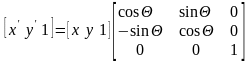 (18)
(18)
полагая

имеем:
 (19)
(19)
Перемножив, получим:

Аналогично тому,
как двумерные преобразования описания
матрицами размером
 ,
трехмерные — могут быть представлены
в виде матриц
,
трехмерные — могут быть представлены
в виде матриц
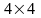 .
И тогда трехмерная точка
.
И тогда трехмерная точка
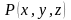 записывается в однородных координатах
как
записывается в однородных координатах
как
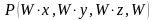 ,
где
,
где
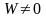 .
Если же
,
то —
.
Если же
,
то —
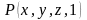 .
.
Поворот
Двумерный поворот,
рассмотренный ранее является в то же
время трехмерным поворотом вокруг оси
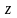 .
.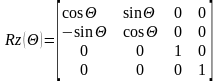
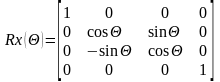
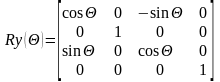
Композиции преобразований
(Двумерных)
При работе с Гибкой
системой объект подвергается сразу
нескольким преобразованиям. Для
получения желаемого результата
используют композицию преобразований,
объединяя матрицы
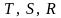 .
К точке более эффективно применять
одно результирующее преобразование,
чем ряд преобразований друг за другом.
.
К точке более эффективно применять
одно результирующее преобразование,
чем ряд преобразований друг за другом.
Рассмотрим, например,
поворот объекта относительно некоторой
точки
 .
.
Но до этого был рассмотрен поворот относительно начала координат. Для решения этой задачи разобьем ее на три части (три элементарных преобразования):
Перенос (точку
 в начало координат),
в начало координат),
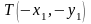 .
.Поворот,
 .
.
Перенос (точку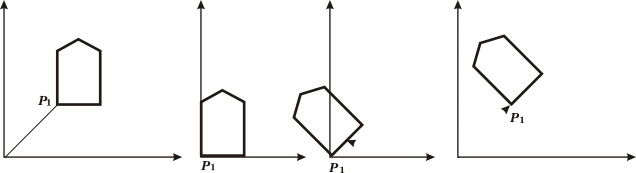
 из начала координат
из начала координат
 назад),
назад),
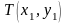 .
.
Результирующее
преобразование имеет вид:
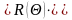 или:
или:
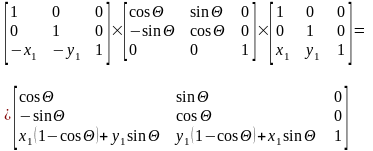
Этот пример хорошо иллюстрирует, как применение однородных координат упрощает задачу.
Аналогично, если надо промасштабировать объект относительно точки , а не начала координат, то надо:
Перенести точку в начало координат, .
Масштабировать,
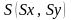 .
.Перенести точку назад, .
Результат имеет вид:
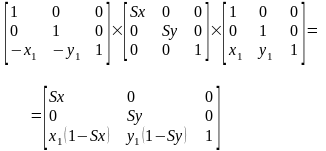
Если нам надо промасштабировать, повернуть и расположить в нужном месте домик. Центром поворота и масштабирования является точка .
Необходимо выполнить:
Перенос (точку в начало координат), .
Масштабирование, .
Поворот, .
Перенос (точку из начала координат назад), .
В структуре данных,
в которой содержится это преобразование,
могут находиться масштабный коэффициент
,
угол поворота
и координаты
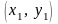 .
Но может быть и записана матрица
результирующего преобразования:
.
Но может быть и записана матрица
результирующего преобразования:
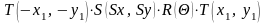 .
.
