Геометрические преобразования. Однородные координаты. Перенос, поворот, масштабирование в однородных координатах. Двумерные преобразования Перенос
Точки на плоскости
можно перенести в позиции путем
добавления к координатам этих точек
констант переноса. Для каждой точки
,
которая перемещается в новую точку
,
сдвигаясь на
единиц по оси
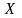и на
— по оси
,
можно написать:
.
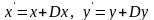(1)
Определим
векторы-строки:
,
тогда уравнения
(1):
,
(2)
или кратко:
.
(3)
Но объект есть множество точек. Его можно переносить, применяя уравнения (1) к каждой его точке. Но каждый отрезок состоит из бесконечного числа точек и этот процесс длился бы бесконечно долго. Удобнее все точки, принадлежащие отрезку перенести путем перемещения одних лишь крайних точек отрезка. И потом вычертить новый отрезок между ними.
Масштабирование
Точки можно
масштабировать (растянуть) в
раз по оси
и в
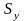— по оси
.
Получим новые точки
с помощью умножения:
. (4)
Определим
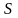как:
,
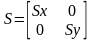можно записать в
матричной форме:
(5)
или
Было применено
неоднородное
масштабирование,
при котором
.
Однородное
масштабирование
не влияет на пропорции.
Поворот
Точки могут быть
повернуты на угол
относительно начала координат. Тогда
координаты точки
:
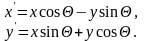
В матричной форме:
(8)
или
(9)
где
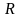— матрица поворота.
Положительное направление — против часовой стрелки, отрицательное — по часовой стрелке.
Однородные координаты
Однородные координаты - это математический механизм, связанный с определением положения точек в пространстве. Привычный аппарат декартовых координат, не подходит для решения некоторых важных задач в силу следующих соображений:
В декартовых координатах невозможно описать бесконечно удаленную точку. А многие математические и геометрические концепции значительно упрощаются, если в них используется понятие бесконечности. Например, "бесконечно удаленный источник света".
С точки зрения алгебраических операций, декартовы координаты не позволяют провести различия межу точками и векторами в пространстве. Действительно, (1,-2,5) - это направление или точка?
Невозможно использовать унифицированный механизм работы с матрицами для выражения преобразований точек. С помощью матриц 3x3 можно описать вращение и масштабирование, однако описать смещение (xў=x+a) нельзя.
Аналогично, декартовы координаты не позволяют использовать матричную запись для задания перспективного преобразования (проекции) точек.
Для решения этих проблем используются однородные координаты.
Преобразования переноса, масштабирования и поворота в матричной форме имеют вид:
Перенос реализуется с помощью операции сложения, а масштабирование и поворот — операции умножения. Удобно было бы эти преобразования представить в единой форме. Рассмотрим как это сделать.
Если мы выразим точки в однородных координатах, то все три преобразования можно реализовать с помощью операции умножения.
В однородных
координатах точка
записывается как
,
где
— масштабный множитель, не равный нулю.
При этом, если точка
задана в однородных координатах
,
то можно найти ее декартовые координаты:
Если же
,
то операция деления не нужна:
