
- •Основные сведения о графических системах (гс). Функции гс. Блок-схема гс. Основные сведения о графических системах (гс).
- •Функции гс
- •Блок-схема гс.
- •Векторный и растровый дисплеи. Получение изображения. Сравнительная характеристика.
- •Геометрические преобразования. Однородные координаты. Перенос, поворот, масштабирование в однородных координатах. Двумерные преобразования Перенос
- •Масштабирование
- •Поворот
- •Однородные координаты
- •Перенос
- •Композиции преобразований
- •(Трехмерных)
- •Преобразование отрезков в растровую форму. Простой, пошаговый алгоритмы, алгоритм Брезенхема.
- •Преобразования, как изменение систем координат.
- •Устранение искажений в растровых изображениях. Выравнивание. Мелкие и движущиеся объекты. Алгоритм By.
- •Заполнение области. Алгоритм построчного сканирования, алгоритм заполнения с затравкой. Заполнение линиями.
- •Растровая развёртка многоуг-в (метод использования когерентности сканируемых строк).
- •Растровая развёртка многоуг-в (метод использования когерентности рёбер).
- •Алгоритм отсечения отрезков Козна и Сазерленда. Алгоритм разбиения средней точкой.
- •Основные виды геометрических моделей.
- •Методы построения геометрических моделей (построение кривых и поверхностей, кусочно-аналитическое описание, кинематический принцип, булевы операции, полигональные сетки).
- •Поперечное сечение криволинейного объекта и его полигональная аппроксимация
- •Методы создания реалистических трехмерных изображений.
- •Получение проекций. Основные виды проекций.
- •Общие сведения об удалении скрытых линий. Сравнительная характеристика алгоритмов.
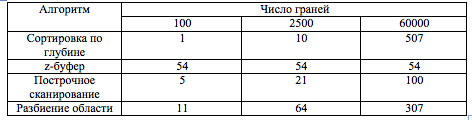
- •Алгоритм сортировки по глубине
- •Алгоритм разбиения области
- •Алгоритм, использующий z-буфер
- •Алгоритм построчного сканирования (пи)
- •Методы закраски полигональной сетки.
- •Фактура. Нанесение узора на поверхность
- •Фактура. Создание неровностей на поверхности.
- •Математическое описание перспективных проекций.
- •Алгоритм трассировки лучей.
- •Общие сведения о свете. Классификация поверхностей по виду отражения.
- •Модель освещения. Свойства объектов
- •4 Типа поверхностей:
- •Отражение диффузное
- •Зеркальное отражение
- •Пропускание света (прозрачность)
- •С рассеянным, диффузным и зеркальным с рассеянным и диффузным с рассеянным светом Без освещения
- •Специальные модели
- •Получение теней.
- •Источник на бесконечности
- •Локальный источник
- •Цвет и его характеристики.
- •Цветовые модели(rgb, cмy).
- •Системы смешивания основных цветов
- •Цветовые модели (hsv, hls). Цветовая гармония.
Алгоритм разбиения области
Гипотеза о способе обработки информации глазом и мозгом.
Когерентность (однородность смежных областей).
Принцип:
область разбивается на окна и в каждом
окне решается вопрос о том, пусто ли
оно или достаточно просто для визуализации;
если это не так, то окно разбивается
дальше до тех пор, пока не станет простым
или его размер не достигнет размера
 .
.
При
 надо максимально 9 разбиений.
надо максимально 9 разбиений.
Конкретная реализация алгоритма зависит от метода разбиения и критерия определения простоты изображения в окне.
Простой вариант 1:
область разбивается последовательно на четыре прямоугольные части;
критерий простоты — объекты не попадают в области.
Алгоритм, использующий z-буфер
Принцип: используются два буфера: регенерации (значения ), z-буфер (z-координата).
Буфер регенерации заполняется значениями при параллельном анализе z-координаты со значениями z-буфера.Шаги:
в z-буфере заносятся максимально возможные значения z;
буфер регенерации заполняется значениями фона;
каждый объект раскладывается в растр;
если
 меньше значения z-буфера
в элементе
меньше значения z-буфера
в элементе
 ,
то:
,
то:
заносится в элемент z-буфера;
значение помещается в элемент буфера регенерации.
Достоинство — простота реализации, нет сортировки.
Недостаток — нужен большой объем памяти по z-буфер.
Объем памяти:
информация о значении
— 24 бита ( ),
информация о глубине 20 бит.
),
информация о глубине 20 бит.
Алгоритм построчного сканирования (пи)
Принцип: расширение алгоритма преобразования многоугольника в растровую форму; разница в том, что имеем дело не с одним многоугольником, а со всеми сразу.
Шаги:
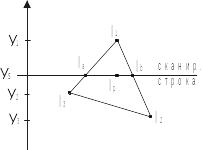
Создается таблица ребер (ТР). Она содержит все ребра многоугольников, отсортированные по меньшей y-координате.
Описание ребра содержит:

создается таблица многоугольников (ТМ).
Описание многоугольников содержит:

Создается ТАР.
Содержит все активные ребра на текущей сканирующей строке. Ребра упорядочены по возрастанию x-координаты.
![]()
Сравнительная характеристика
Методы закраски полигональной сетки.
Однотонная закраска.
Вычисляется 1 уровень
 ,
который используется для закраски
всего многоугольника. При этом
предполагается, что:
,
который используется для закраски
всего многоугольника. При этом
предполагается, что:
Источник света расположен в бесконечности (
 на всей полигональной грани)
на всей полигональной грани)Наблюдатель находится в бесконечности (
 на всей полигональной грани)
на всей полигональной грани)Многоугольник представляет реальную моделируемую поверхность, а не является аппроксимацией криволинейной поверхности.
Если 1) или 2)
неприемлемо, можно использовать
усредненное значение
 ,
,
 вычисленные в центре многоугольника.
вычисленные в центре многоугольника.
3-е предположение тоже часто не выполняется, но оно оказывает большое влияние на результат: каждая из видимых граней аппроксимированной поверхности хорошо отличима от других, т.к. каждой из этих граней отличается от соседних граней (эффект полос Маха).
Интерполяция
интенсивностей (метод Гуро).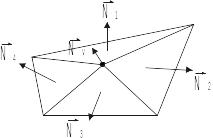
Процесс закраски осуществляется в 4 этапа:
Вычисляются нормали к поверхностям.
Определяются нормали в вершинах путем усреднения нормалей по всем граням, которым принадлежит вершина.

Используя нормали в вершинах и применяя произвольный метод закраски, вычисляются значения в вершинах.
Каждый многоугольник закрашивается путем линейной интерполяции значений в вершинах сначала вдоль каждого ребра, а затем между ребрами вдоль каждой сканирующей строки:

Интерполяция векторов нормали (метод Фонга).
Закраска Фонга требует больших вычислительных затрат, но она позволяет разрешить многие проблемы метода Гуро. При закраске Гуро вдоль сканирующей строки интерполируется значение , а при закраске Фонга – вектор нормали. Затем он используется в модели освещения для вычисления . При этом достигается лучшая локальная аппроксимация кривизны поверхности, и получается более реалистичное изображение. Особенно правдоподобно выглядят зеркальные блики.
Этапы закраски:
Вычисляются нормали к поверхностям.
Определяются нормали в вершинах путем усреднения нормалей по всем граням, которым принадлежит вершина.
Для каждой точки сканирующей строки определяется вектор нормали путем линейной интерполяции значений N (сначала в вершинах, затем - между ребрами).
Для каждой точки сканирующей строки вычисляется значение .
Метод Фонга приводит к более качественным результатам, т.к. аппроксимация нормали осуществляется в каждой точке. Уменьшаются полосы Маха.
