Тақырып 9. Дискретті кездейсоқ шамаларды модельдеу әдістері
СОӨЖ тапсырма
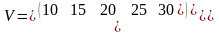кестесімен
берілген v
кездейсоқ
шамасыньң 2
нақтыламаларын
алу қажет.
екені белгілі. Сондай-ақ алгоритмнің
блок-схемасын келтіріңіз.
СОӨЖ өткізу түрі: тренинг.
Әдістемелік ұсыныс:
Бақылау
мысалы.
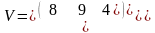кестесімен берілген V
кездейсоқ
шамасының 4нактымаларын алу қажет.
z1
=
0,5753; z2
= 0,4279;
z3=
0,1534, z3
=
0,8412 екені белгілі.
Шешуі.
Дискретті кездейсоқ шаманы модельдеу үшін 2-теореманы қолданамыз. Ол үшін [0, 1] аралығын 3 кесіндіге бөлеміз (23-сурет).
Δ1 Δ2 Δ3
I_____________I______________І___________I
0 0,3 0,75 1
23-сурет
2-теоремаға сәйкес аламыз:
Бақылау нысаны: есеп беру
Тапсырманы орындауды бағалау баллы – 4б
Ұсынылатын әдебиет: 1нег [33-35], Знег [539-547], бқос [50-57], 8қос [23-24]
Тақырып 10. Арнаулы үлестірім заңдылықты дискретті кездейсоқ шамаларды модельдеу әдістері
СОӨЖ тапсырма:
Келесі бастапқы мәндерде Пуассон үлестіріміне бағынатын v кездейсоқ шамасьның 2 нақтыламаларын алу қажет: λ= 0,6; р= 0,3; z1 - 0,15; z2 = 0,72; z3= 0,14; z4 = 0,25.
СОӨЖ өткізу түрі: тренинг.
Әдістемелік ұсыныс:
Бақылау мысалы. Келесі бастапқы мәндерде Пуассон үлестіріміне бағынатын v кездейсоқ шамасының 2 нақтыламаларын алу қажет: λ = 1,6; р= 0,4; z1 = 0,15; z2 = 0,72; z3 = 0,14; z4 = 0,25; z5 = 0,35; z6 = 0,51; z7 = 0,97; z8 = 0,53.
Шешуі.
Сынақтар санын табайық: п = λ/р = 1,6/0,4 = 4.
4 тәуелсіз сынақтан тұратын сериялар өткізейік, олардың әрқайсысында оқиға р ықтималдықпен орындалады, және i нөмірлі сериядағы А оқиғасының орындалу жағдайларының ki санын есептейік ki сандары Пуассон үлестірімінің нактыламасы болып табылады:
Серия 1:
Серия
2:
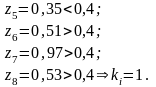
Сонымен, х1 = 3, х2 = 1 .
Бақылау нысаны: есеп беру
Тапсырманы орындауды бағалау баллы – 4б
Ұсынылатын әдебиет: 1нег [33-35], Знег [539-547], бқос [50-57], 8қос [23-24]
Тақырып 11. Көпөлшемді кездейсоқ шамаларды модельдеудің тізбектелген әдісі
СОӨЖ тапсырма:
Тығыздық
функциясы
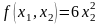болатын η=(η1,η2)
екіөлшемді кездейсоқ вектордың 1
нақтыламасын табу керек, ол х1
+ х2
< 2,
х1
> 0,
х2>
0
үшбұрышындағы мәндерді қабылдай алады.
z
мәндерін
орта шаршы алгоритм көмегімен алыңыз.
СОӨЖ өткізу түрі: тренинг.
Әдістемелік ұсыныс: Бақылау мысалы. Тығыздық функциясы f(х1 ,х2)=6х22 болатын η=(η1,η2) екіөлшемді кездейсоқ вектордың 1 нақтыламасын табу керек, ол х1+х2<1, х1 > 0, х2 > 0 үшбұрышындағы мәндерді қабылдай алады, егер z1 = 0,027; z2 = 0,250.
Шешуі.
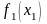мен
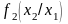анықгайық:
Сонда кері функция әдісі теңдігінен
анықтаймыз
z мәндерін орнына қойьш, аламыз:
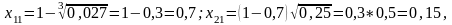яғни
х [1] =(0,7; 0,15).
Бақылау нысаны: есеп беру
Тапсырманы орындауды бағалау баллы – 4б
Негізгі әдебиет: 1 [36-41], 3 [548-552]
Қосымша әдебиет: 6 [50-57], 8 [19-20]
Тақырып 12. Нейманның жалпылама "шығарып тастау" әдісі
СОӨЖ тапсырма:
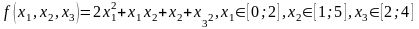тығыздық
функциялы
үшөлшемді
кездейсоқ вектордың 1 нақтыламасын табу
керек. z
мәндерін
шегерінділер әдісінің толық алгоритмі
көмегімен алыңыз.
СОӨЖ өткізу түрі: тренинг.
Әдістемелік ұсыныс: Бакылау мысалы. Тығыздық функциясы келесі түрдегі үшөлшемді кездейсоқ вектордың 1 нақтыламасын табу керек, егер z1 =0, 1 ; z2 = 0,2; z3 = 0,4; z4 = 0, 1 5 болса:
Шешуі.
Есепті Нейманның жалпылама "шығарып тастау" әдісі көмегімен шешеміз.
Z1=0,1 ;z2=0,2; z3=0,4; z4=0,15есептейміз.
Келесі мәндерді табайық:
Х1=a1+z1(b1-a1)=0+0,1*(2-0)=0,2;
X2=a2+z2(b2-a2)=1+0,2*(3-1)=1,4;
X3=a3+z3(b3-a3)=2+0,4*(5-2)=3,2.
X1 ,x2 ,,x3 нүктелеріндегі функция мәнін есептейік.
Сонымен х [1] = (0,2; 1,4; 3,2).
Бақылау нысаны: есеп беру
Тапсырманы орындауды бағалау баллы – 4б
Негізгі әдебиет: 1 [36-41], 3 [548-552]
Қосымша әдебиет: 6 [50-57], 8 [19-20]
Тақырып 13. Стационарлнқ емес кездейсоқ процестерді модельдеу
СОӨЖ тапсырма:
M
x
математикалык
үміті мен R
x
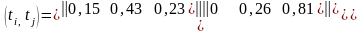корреляциялык
матрицасымен
берілген қалыпты стационарлы емес
процесті модельдеу керек.
СОӨЖ өткізу түрі: тренинг.
Әдістемелік үсыныс:
М
х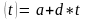
математикалық
үміті мен R
x
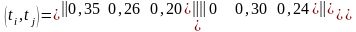корреляциялық матрицасымен берілген
қалыпты стационарлы емес процесті
модельдеу керек.
Шешуі.
(43) жөне (44) формулаларымен координатты функциялар мен дисперсияларды есептейік:
D1=Rx(t1,t1)=0,35;
φ1(t1)=Rx(t1,t1)/D1=0,35/0,35=1;
φ1(t2)=Rx(t1,t2)/D1=0,26/0,35=0,743;
φ1(t3)=Rx(t1,t3)/D1=0,2/0,35=0,571;
D2=Rx(t2,t2)-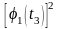
D1=0,1068;
φ2(t1) = 0;
φ2(t2) =1;
φ2(t3)
=
D3=Rx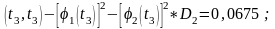
φ3(t1)=0;
φ3(t2)=0;
φ3(t3)=1;
олай болса, x(tj) нақтыламасын есептеу үшін келесі формулаларды қолданамыз:
x( t1 ) = a + bt1 + y1;
x( t2 ) = a + bt2 + 0,743 y1 + y2;
x( t3 ) =a + bt3 +0,571 y1+ 0,8568y2+ y3.
Бақылау нысаны: есеп беру
Тапсырманы орындауды бағалау баллы – 4б
Ұсынылатын өдебиет: Інег [42-47], [36-41], З нег [548-552], ,6қос [50-57], 8қос [19-20]