Тақырып 6,7. Үздіксіз кездейсоқ шамаларды модельдеу әдістері

СОӨЖ тапсырма:

1. Тығыздық функциясы f(х) = 3х ⁴ болатын η кездейсоқ шамасының 2 нақтыламаларын табу керек, мұнда

2. Тығыздық функциясы түрінде берілген η кездейсоқ шамасының 2 нақтыламаларын табу керек , болсын.

3.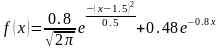 тығыздық функциясымен берілген η кездейсоқ шамасьның нақтыламасын табу керек. 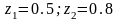болсын.

СОӨЖ өткізу түрі: тренинг.

Әдістемелік ұсыныс: Бақылау мысалы 1 . Тығыздық функиясы f(х) = х болатын η кездейсоқ шамасыньң 1 нақтыламасын табу керек, мұнда,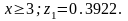

Шешуі.

Есепті кері функция әдісімен шешеміз, бұл үшін х_j қатысты теңдікті шешеміз:

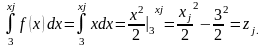
Бақьлау мысалы 2. f(x) = 0,72е^-2.4x + 0,56(1 -0,4x) тығыздық функциясымен берілген η кездейсоқ шамасының нақгыламасын тбу керек, z₁= 0,55; z₂= 0,49 болсын.

Шешуі.

Тығыздық функциясы күрделі түрде болғандықтан, берілген есепті шешу үшін композиция әдісі ыңғайлы. Берілген тығыздық функциясын қарапайымдау тығыздық функцияларының композициясы ретінде қарастырайық:

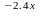Сонымен С₁₌0.3; C₂₌0.7; f_{1 =}2.4e ; f₂

6 – теореманы қолданып аламыз:

Z₁₌0.55 оқиғасы орындалды. Сондықган кездейсок шаманы модельдеу үшін f₂ тығыздық функциясын қолданайык, яғни x₁₌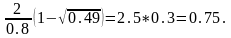

Бакылау мысалы 3. Тығыздық функциясы f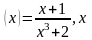 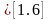болатын кездейсоқ шамасының 2 нақтыламаларын табу керек, z₁₌0.4372; z₂₌0.1246; z₃₌0.3392; z₄=0.7535 болсын.

Шешуі.

Есепті шешу үшін Нейманньщ «шығарып тастау» әдісін қолданмыз. М параметрін анықтайық:

М=SUPf

x₁ = 1+ 0.4372* =1+2.186 = 3.186; y_{1 =} 0.67 * 0.1246 = 0.0835;

f

y₁= 0.0835< f = 0.1219.

Олай болса, η= x₁ = 3.186.

x₂=1+0.3392*5=1+1.696=2.696; y₂=0.67*0.7535=0.5048;

f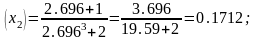

y₂=0.5048>f =0.1712.

Олай болса, x₂ ескерілмейді.

Бақылау нысаны: есеп беру

Тапсырманы орындауды бағалау баллы – 8б

Ұсынылатын әдебиет: Інег [22-32], Знег [506-538], 6қос [42-49], 8қос [24-29]

Тақырып 8. Арнаулы үлестірім заңдылықты үздіксіз кездейсоқ шамаларды модельдеу әдістері

СОӨЖ тапсырма:

1. Тығыздық функциясы f түрінде болатыя кездейсоқ шаманың 2 нақтыламаларын алыңыз. z мәнін шегерінділер әдісінің қысқартылған алгоритмі көмегімен есептеңіз.

2. Тығыздық функциясы f(х) =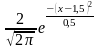 түрінде болатын кездейсоқ шаманың 1 нақтыламасын альңыз. z мәнін орта кебейтінді алгоритмі көмегімен есептеңіз.

СОӨЖ өткізу түрі: тренинг.

Әдістемелік ұсыныс: Бақылау мысалы 1. Тығыздық функциясы f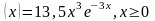 түрінде болатын η кездейсоқ шамасының 1 нақтыламасьш алыңыз, егер z₁₌,.2; z₂=0,4; z₃=0,3; z₄=0,5.

Шешуі.Тығыздық функциясы f түрінде болатын η кездейсоқ шамасының гамма-үлестірімге бағынады. Келесі параметрлерді табайьқ: α=3, k=4.

Сонымен кездейсоқ шаманың нақтыламасьн келесі формуламен есептеуге болады:

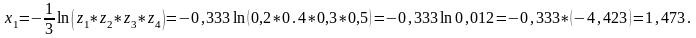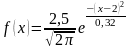
Бақылау мысалы 2. Тығыздық функциясы болатын кездейсоқ шаманың 1 нақтыламасын алыңыз, егер

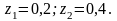
Шешуі.

түріндегі тығыздық функциясы бар η кездейсоқ шамасы қалыпты үлестірімге бағынады. Келесі параметрлерді табайық: т_х = 2,δ_Х = 0,4.

Марсаль алгоритмі көмегімен кездейсоқ шаманың нақтыламасын табамыз.

Есептейік: v ₁ = 2* z₁ = 2*0,2 = 0,4; v ₂= 2* z₂- 1 = 2*0,4- 1 = -0,2;

S= 0,4² + (-0,2)² = 0,2 < 1.

Х₁ нақтыламасын келесі формуламен табамыз:

Бақылау нысаны: есеп беру

Тапсырманы орындауды бағалау баллы – 4б

Ұсынылатын әдебиет: 1нег [22-32], Знег [506-538], бқос [42-49], 8қос [24-29]