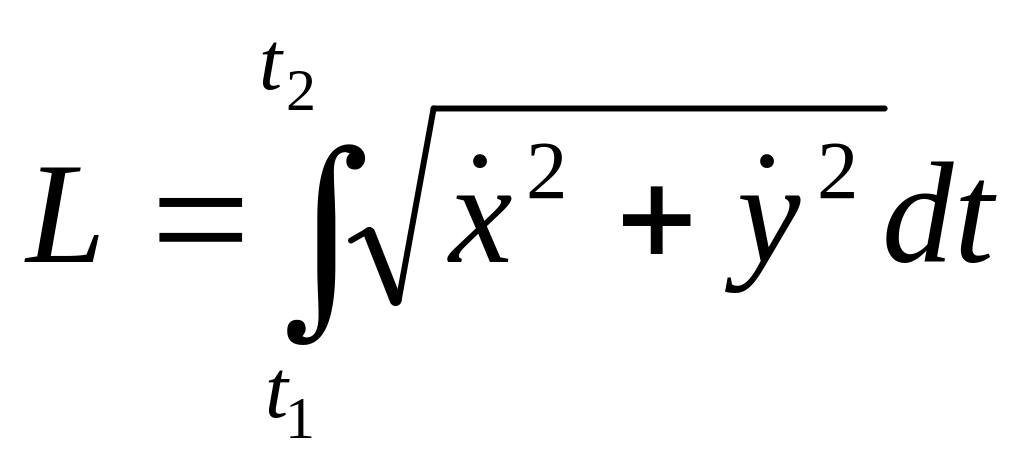.

Если гладкая кривая задана в полярных координатах уравнением , , то длина дуги равна

.

Пример 12. Найти длину дуги кривой от до .

Дифференцируя уравнение кривой, имеем:

.

Таким образом,

.

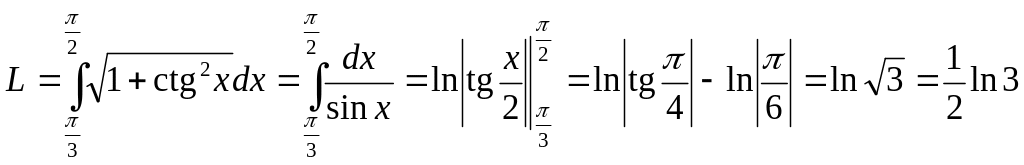Пример 13. Найти длину дуги кривой , от до .

Вычислим производные по параметру t: , . Следовательно,

.

Пример 14. Найти длину дуги кривой от до .

Имеем . Следовательно,

.

Примеры для самостоятельной работы

Вычислить длины дуг кривых:

21. от х = 0 до х = 1.

22. от х = 0 до .

23. от х = 0 до х = 1.

24. 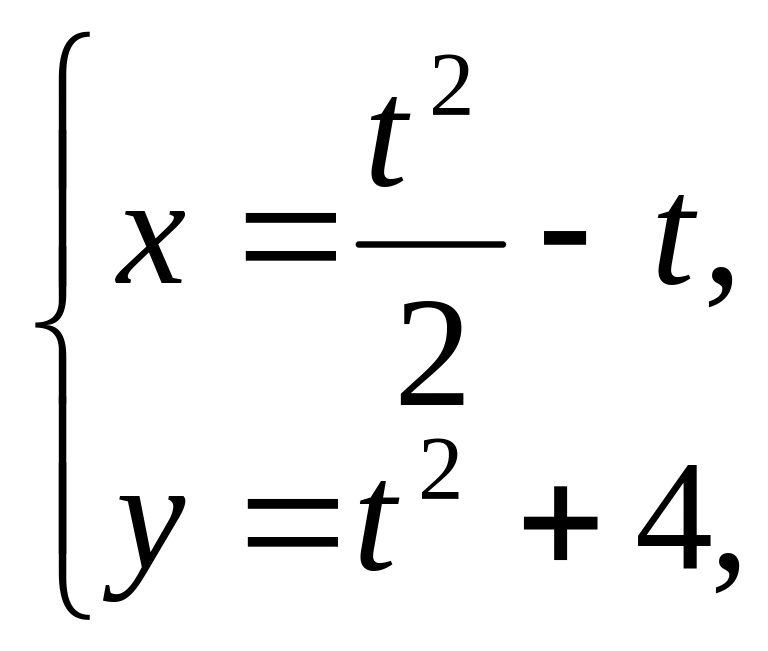от t = 0 до t = 4.

25. . от t = 0 до t = 1.

26. от t = 0 до t = .

27. .

28. от  = 0 до .

29. .

1.4. Вычисление объема тела Вычисление объема тела по известным площадям поперечных сечений

Если площадь сечения тела плоскостью, перпендикулярной оси Ох, может быть выражена как функция от х, т.е. в виде , , то объем части тела, заключенной между перпендикулярными оси Ох плоскостями, и , находится по формуле

.

Пример 15. Найти объем тела, в основании которого лежит равнобедренный треугольник с высотой h и основанием а. Поперечное сечение тела есть сегмент параболы с хордой, равной высоте сегмента (см. рис. 4).

Р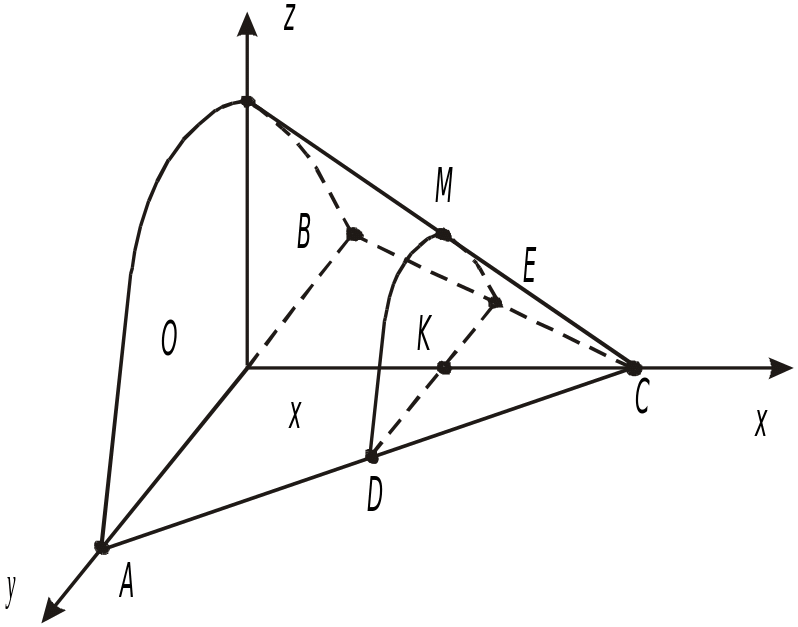 ис. 4

По условию задачи имеем , , , . Выразим площадь поперечного сечения как функцию от х, для чего предварительно найдем уравнение параболы. Длину хорды DE можно получить из подобия треугольников и , а именно или , т.е. .

Положим , тогда уравнение параболы в системе координат uOv примет вид . Отсюда находим площадь поперечного сечения данного тела:

,

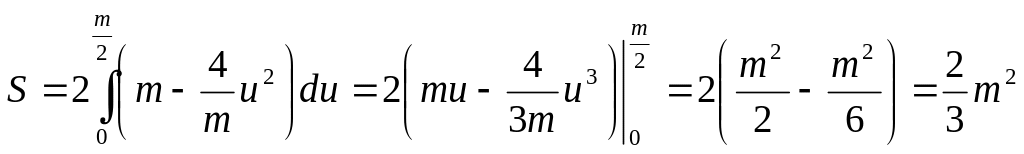или

.

Таким образом,

.

Вычисление объема тела вращения

Если криволинейная трапеция, ограниченная кривой и прямыми , , , вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле

.

Если фигура, ограниченная кривыми , и прямыми , вращается вокруг оси Ох, то объем тела вращения

.

Пример 16. Вычислить объем тела, образованного вращением относительно оси Ох фигуры, ограниченной кривыми и (рис. 5).

Рис. 5

Определяем точки пересечения данных кривых. Для этого решаем уравнение , откуда , т.е. , . Следовательно,

.

Примеры для самостоятельной работы

Найти объемы тел, образованных вращением вокруг оси Ох фигур, ограниченных линиями:

30. , . 31 , х = 1, у = 0.

32. , . 33. , .

34. В цилиндрический стакан с водой вложен параболоид вращения вершиной вниз. Основание и высота параболоида совпадают с основанием и высотой цилиндра. Найти объем оставшейся в стакане воды, если радиус равен а, а высота - b.

35. Найти объем тела, ограниченного плоскостями х = 1, х = 3, если площадь его поперечного сечения обратно пропорциональна квадрату расстояния сечения от начала координат, а при х = 2 площадь сечения равна 27 (кв. ед.).

1.5. Вычисление площади поверхности вращения

Если дуга гладкой кривой вращается вокруг оси Ох, то площадь поверхности вращения вычисляется по формуле

.

Если кривая задана параметрическими уравнениями , , то

.

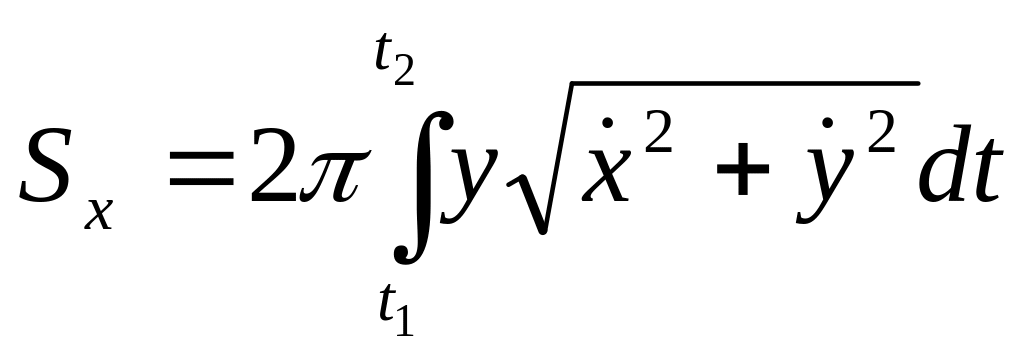Пример 17. Найти площадь поверхности, образованной вращением, вокруг оси Ох дуги кривой от до .

Находим , тогда

.

Произведем замену переменной , . Определяем пределы интегрирования по t: если , то ; если , то . Таким образом,

.

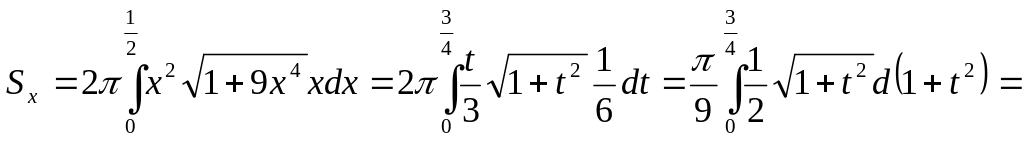
Примеры для самостоятельной работы

Найти площади поверхностей, образованных вращением вокруг оси Ох дуг кривых:

36. от х = 0 до . 37. от х = 1 до х = 3.

38. , х = 5, х  0. 39. , .

1.6. Приложения определенных интегралов Статические моменты инерции и моменты инерции плоских фигур и дуг

Пусть на плоскости хОу задана система материальных точек , , …, с массами , , …, .

Определение 3. Статическим моментом этой системы относительно оси Ох называется сумма произведений масс этих точек на их ординаты:

.

Аналогично (как сумма произведений масс точек на их абсциссы) определяется статический момент системы относительно оси Оу:

.

Определение 4. Моментами инерции и системы относительно осей Ох и Оу называются суммы произведений масс точек на квадраты их расстояний от соответствующей оси. Таким образом,

, .

При этом за статические моменты и моменты инерции плоских фигур и дуг принимают соответствующие моменты условных масс, равномерно распределенных вдоль этих дуг и фигур с плотностью (линейной или плоскостной), равной единице.

Статические моменты и моменты инерции дуги плоской кривой выражаются по формулам:

, , , ,

где - дифференциал дуги кривой.

Статические моменты и моменты инерции криволинейной трапеции, ограниченной кривой , осью Ох и двумя прямыми , , вычисляются по формулам:

, ,

, .

Здесь - дифференциальная площадь криволинейной трапеции.

Пример 18. Найти статический момент и момент инерции полуокружности относительно оси Ох.

Статический момент будем вычислять по формуле , где , а . Тогда

.

Находим момент инерции относительно оси Ох:

.

Введем подстановку , ; если то ; если , то . Следовательно,

.

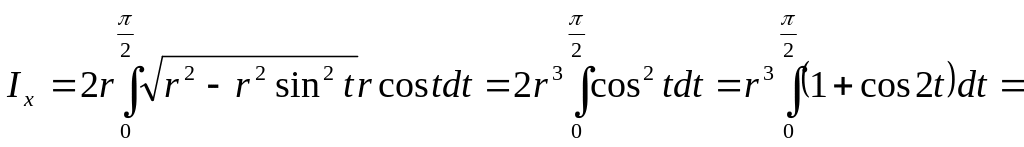
Пример 19. Найти момент инерции площади эллипса , относительно оси Оу.

Момент инерции площади эллипса относительно оси Оу равен , где . Из параметрических уравнений эллипса находим: , откуда, учитывая, во-первых, что - функция четная; а, во-вторых, что если , то ; если , то , получим

.

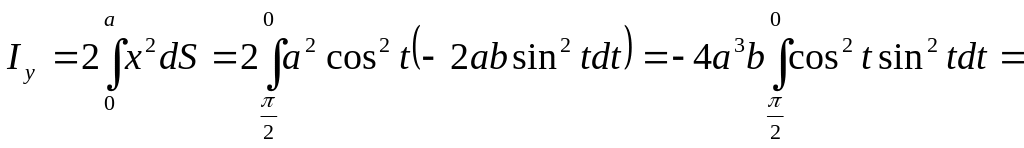
Примеры для самостоятельной работы

40. Найти статические моменты и моменты инерции дуги астроиды , , лежащей в I четверти.

41. Найти момент инерции параболического сегмента, ограниченного параболой и прямой у = 3, относительно оси Ох.

42. Найти момент инерции и статический момент прямоугольника со сторонами а и b относительно осей симметрии прямоугольника.

43. Найти полярный момент инерции круга диаметром d, т.е. момент инерции относительно оси, проходящей через центр круга и перпендикулярной его плоскости.