5. Вычислить двойной интеграл

, .

Область интегрирования D ограничена прямой , кубической параболой и ветвью параболы , расположенной ниже оси Ох. Так как любая вертикальная прямая пересекает границу области только в двух точках:

в точке входа , в которой и в точке выхода , в которой , то область D можно задать в виде системы неравенств: Тогда, используя формулу: , где

получаем:

Сначала вычисляем внутренний интеграл по , считая постоянной величиной

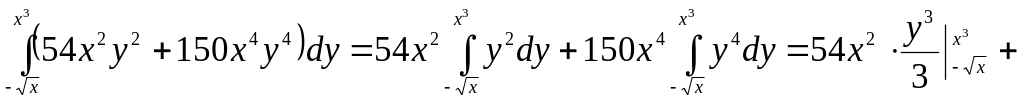
Далее вычисляем внешний интеграл

.

Ответ:

6. Найти площадь фигуры, ограниченной данными линиями:

а)

б) .

а)

Площадь области равна величине двойного интеграла, вычисленного по области интегрирования. Область интегрирования ограничена дугами окружностей , и лучами, идущими из начала координат под углами . Так как область ограничена дугами окружностей, то проще вычислять двойной интеграл в полярной системе координат.

Уравнение окружности в полярной системе координат . Уравнение окружности в полярной системе координат .

Ответ:

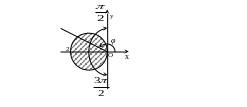
б) .

Построим область интегрирования D. Имеем:

- окружность с центром в точке и радиусом 3.

- окружность с центром в точке и радиусом 5.

- прямая, проходящая через начало координат, образующая с положительным направлением оси угол . - прямая, проходящая через начало координат, образующая с положительным

направлением оси угол .

Так как область интегрирования представляет собой часть круга, то удобно перейти к полярным координатам. Подставляя в уравнения окружностей , получаем их полярные уравнения:

.

.

Следовательно, область интегрирования D в полярных координатах можно задать неравенствами:

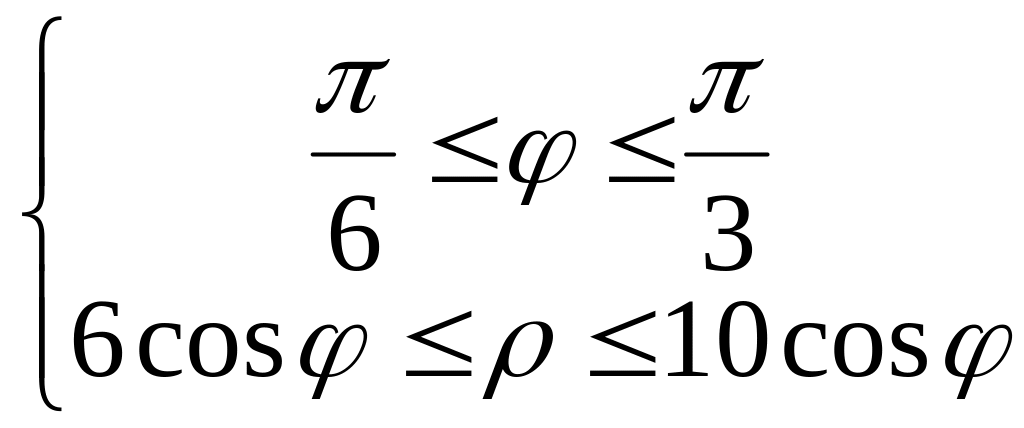
Используя формулу перехода к полярным координатам, получаем

.

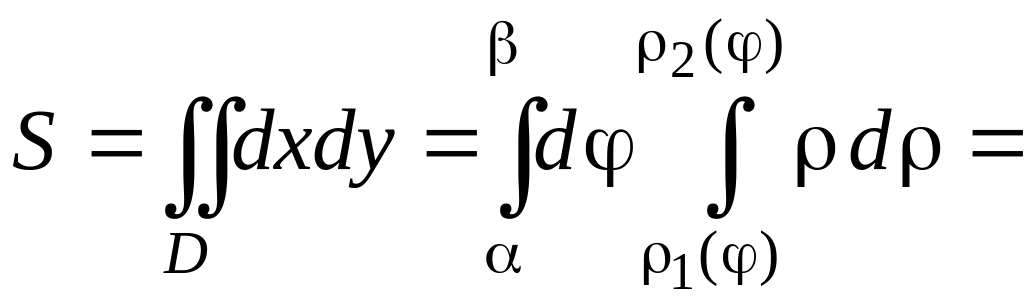
Ответ: .

7. Вычислить объем тела, заданного ограничивающими его поверхностями:

а)

б)

Объем тела равен величине тройного интеграла, вычисленного по области интегрирования. Область интегрирования ограничена по бокам цилиндрическими поверхностями , , снизу плоскостью ОХУ , сверху конической поверхностью . При данных границах области тройной интеграл проще вычислить в цилиндрической системе координат.

Уравнение цилиндрической поверхности в цилиндрической системе координат . Уравнение цилиндрической поверхности в цилиндрической системе координат . Уравнение конической поверхности в цилиндрической системе координат .

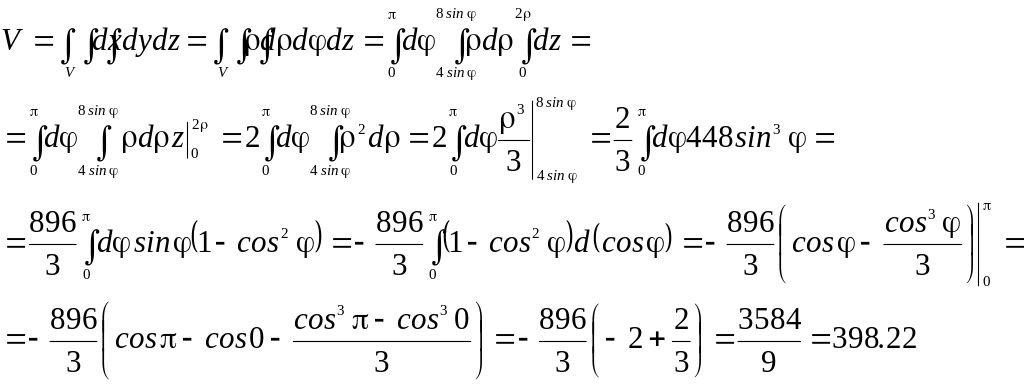
Ответ:

б)

Объем тела вычисляется по формулу:

Тело V ограничено снизу плоскостью , сверху параболическим цилиндром , боковая поверхность - круговой цилиндр с центром в точке и радиусом 1, .

Для вычисления интеграла удобно перейти к цилиндрическим координатам: .

Запишем уравнения границ в цилиндрических координатах:

1) ;

2)

.

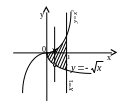
Пределы изменения координат φ и ρ определяем по виду проекции области интегрирования V на плоскость xOy (Рис. 24). Пределы изменения угла φ будут от до . При любом фиксированном угле φ, полярный радиус ρ изменяется от 0 до (уравнение окружности). При каждом значении (φ,ρ) в области D значение координаты z для области V меняются от до .

Таким образом,

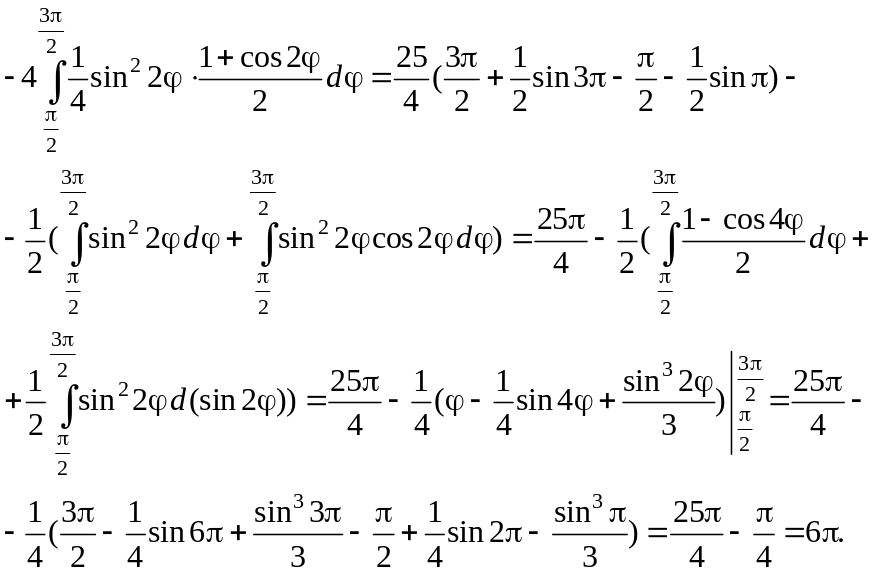
Ответ: .