КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ

Группа 1190у

Второй семестр

Преподаватель Бублинова В.В.

Методички:

Романов А.Д., Черткова О.В. Дифференциальное исчисление функций одной и многих переменных. Интегральное исчисление функций одной переменной. Учебное пособие. – Северодвинск: РИО Севмашвтуза, 2005. - 84 с.

Романов А.Д., Агибалова О.Д. Кратные интегралы. Векторный анализ. Дифференциальные уравнения. Учебное пособие. Северодвинск: Севмашвтуз, 2006, - 86 с.

ВАРИАНТ №1

1. Вычислить интеграл

2. Вычислить интеграл с помощью подстановки .

3. Вычислить интеграл, интегрируя по частям, .

4. Вычислить интеграл .

5. Найти определенный интеграл по формуле Ньютона-Лейбница

.

1. Изобразить на плоскости область и изменить порядок интегрирования:

.

2. Вычислить двойной интеграл

3. Найти площадь фигуры, ограниченной данными линиями:

.

4. Вычислить объем тела, заданного ограничивающими его поверхностями:

.

5. Найти координаты центра масс однородных плоских фигур, ограниченных кривыми ,

1. Найти градиент скалярного поля

2. Найти производную функции в точке по направлению S

M₀(1; 1; 1) S = (2; -4; 4)

3. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя)

, , , ,

4. Найти циркуляцию векторного поля вдоль контура Г (в направлении, соответствующем возрастанию параметра t) ( )

,

1. Найти общее решение дифференциального уравнения:

.

2. Найти общее решение дифференциального уравнения:

3. Решить задачу Коши для дифференциального уравнения:

.

4. Найти общее решение дифференциального уравнения:

5. Найти общее решение дифференциального уравнения:

.

ВАРИАНТ №2

1. Вычислить

2. Вычислить интеграл с помощью подстановки .

3. Вычислить интеграл, интегрируя по частям, .

4. Вычислить интеграл .

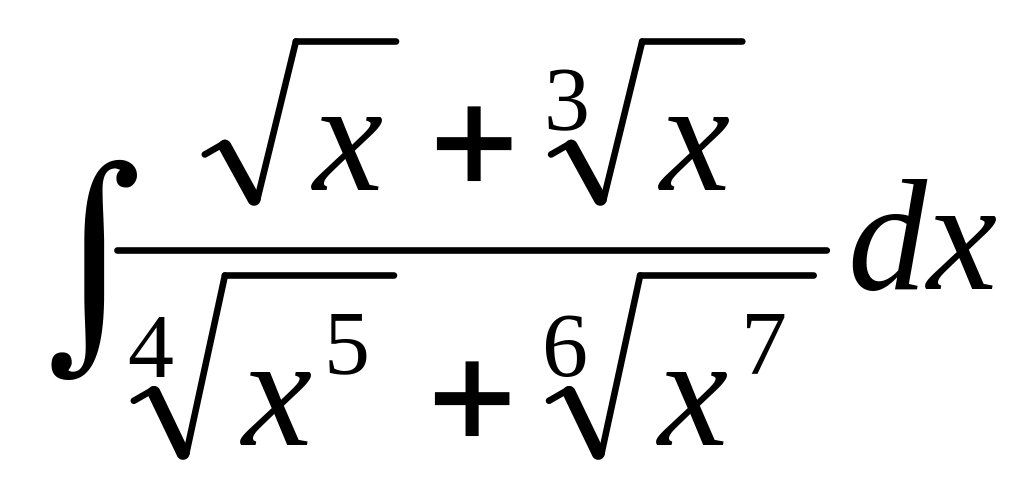5. Найти определенный интеграл по формуле Ньютона-Лейбница

.

1. Изобразить на плоскости область и изменить порядок интегрирования:

.

2. Вычислить двойной интеграл

3. Найти площадь фигуры, ограниченной данными линиями:

.

4. Вычислить объем тела, заданного ограничивающими его поверхностями:

.

5. Найти координаты центра масс однородных плоских фигур, ограниченных кривыми ,

1. Найти градиент скалярного поля

2. Найти производную функции в точке по направлению S

M₀(1; 1; 1) S = (2; 2; 2)

3. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя)

, , ,

4. Найти циркуляцию векторного поля вдоль контура Г (в направлении, соответствующем возрастанию параметра t) ( )

,

1. Найти общее решение дифференциального уравнения:

.

2. Найти общее решение дифференциального уравнения:

3. Решить задачу Коши для дифференциального уравнения:

.

4. Найти общее решение дифференциального уравнения:

5. Найти общее решение дифференциального уравнения

.

ВАРИАНТ №3

1. Вычислить

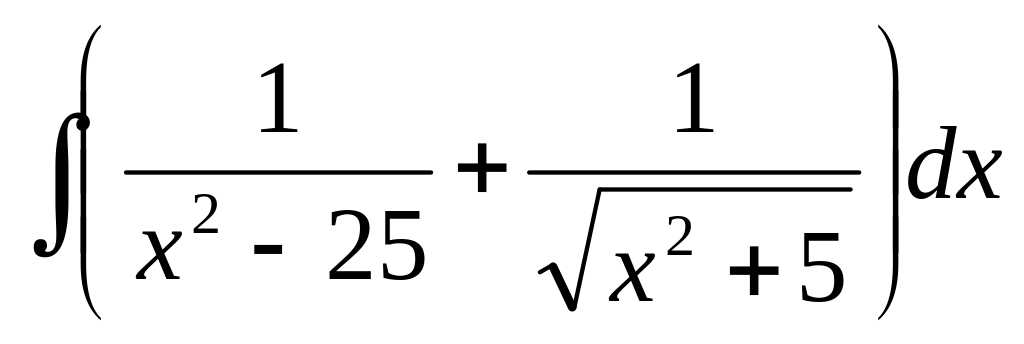
2. Вычислить интеграл с помощью подстановки .

3. Вычислить интеграл, интегрируя по частям, .

4. Вычислить интеграл .

5. Найти определенный интеграл по формуле Ньютона-Лейбница

.

1. Изобразить на плоскости область и изменить порядок интегрирования:

.

2. Вычислить двойной интеграл

3. Найти площадь фигуры, ограниченной данными линиями:

.

4. Вычислить объем тела, заданного ограничивающими его поверхностями:

.

5. Найти координаты центра масс однородных плоских фигур, ограниченных кривыми ,

1. Найти градиент скалярного поля

2. Найти производную функции в точке по направлению S

M₀(1; 2; 1) S = (2; -1; 2)

3. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя)

4. Найти циркуляцию векторного поля вдоль контура Г (в направлении, соответствующем возрастанию параметра t)

,

1. Найти общее решение дифференциального уравнения:

.

2. Найти общее решение дифференциального уравнения:

3. Решить задачу Коши для дифференциального уравнения:

.

4. Найти общее решение дифференциального уравнения:

5. Найти общее решение дифференциального уравнения

.

ВАРИАНТ №4

1. Вычислить

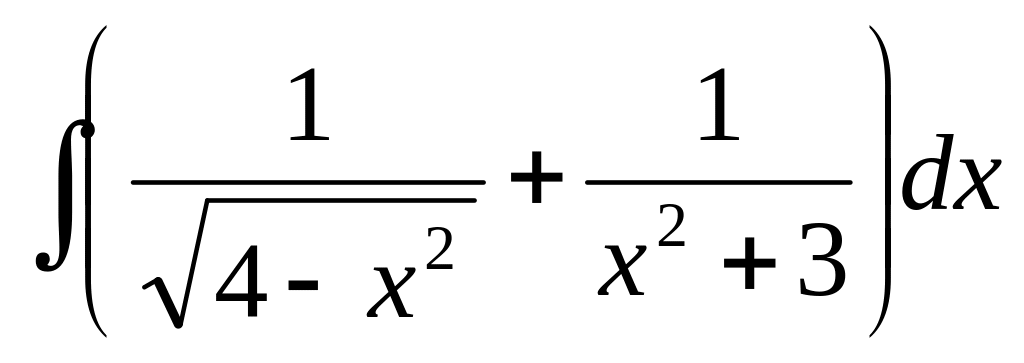
2. Вычислить интеграл с помощью подстановки .

3. Вычислить интеграл, интегрируя по частям, .

4. Вычислить интеграл .

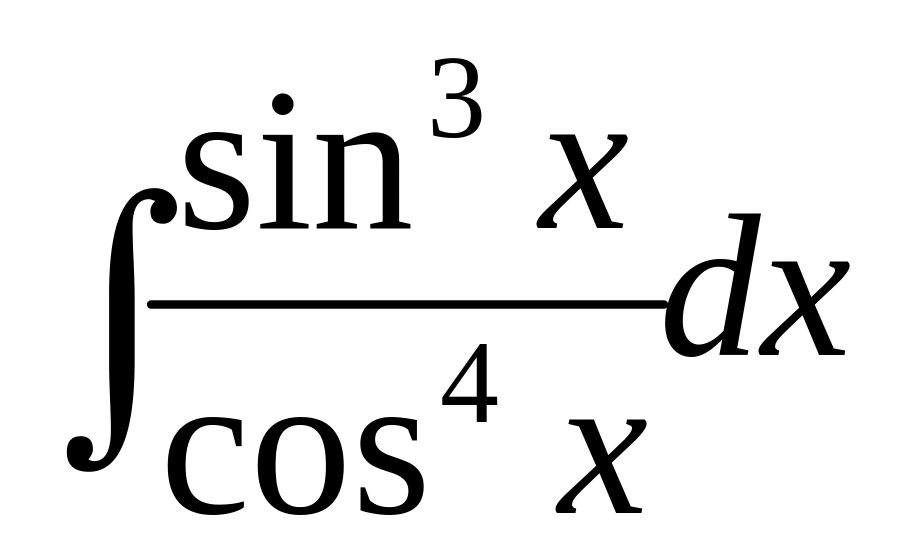5. Найти определенный интеграл по формуле Ньютона-Лейбница

.

1. Изобразить на плоскости область и изменить порядок интегрирования:

.

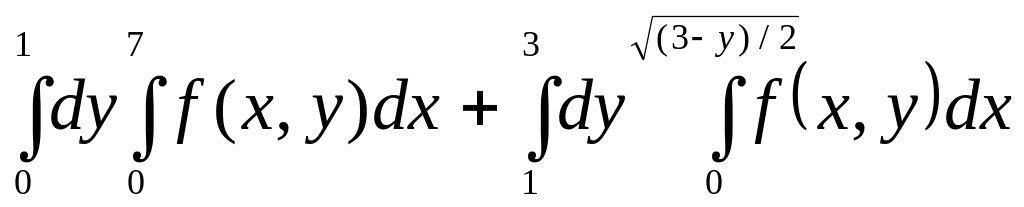2. Вычислить двойной интеграл

3. Найти площадь фигуры, ограниченной данными линиями:

.

4. Вычислить объем тела, заданного ограничивающими его поверхностями:

.

5. Найти координаты центра масс однородных плоских фигур, ограниченных кривыми ,

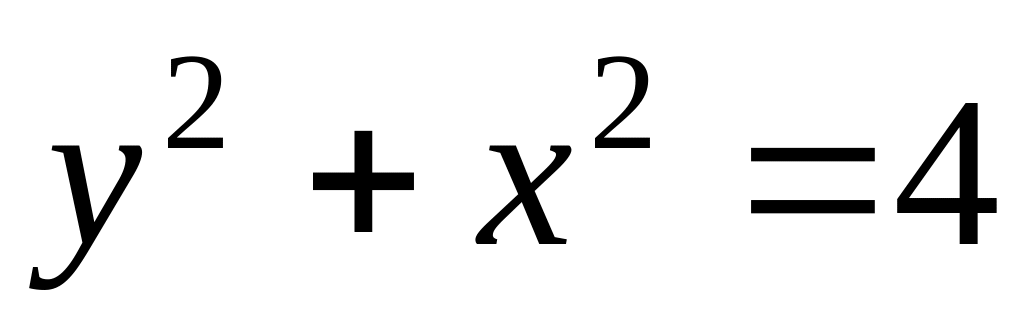1. Найти градиент скалярного поля

2. Найти производную функции в точке по направлению S

M₀(1; 1; 2) S = (2; 2; 1)

3. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя)

, ,

4. Найти циркуляцию векторного поля вдоль контура Г (в направлении, соответствующем возрастанию параметра t)

,

1. Найти общее решение дифференциального уравнения:

.

2. Найти общее решение дифференциального уравнения

3. Решить задачу Коши для дифференциального уравнения:

.

4. Найти общее решение дифференциального уравнения:

5. Найти общее решение дифференциального уравнения

.

ВАРИАНТ №5

1. Вычислить

2. Вычислить интеграл с помощью подстановки .

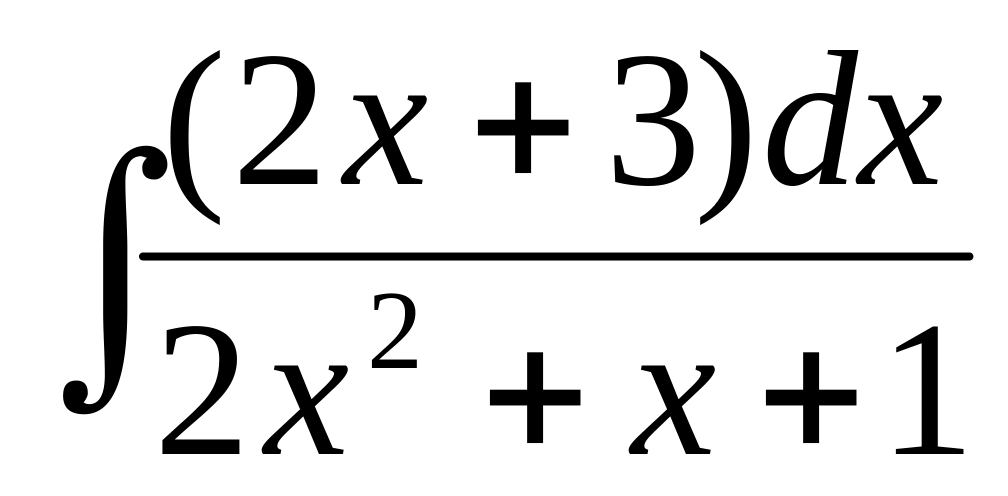3. Вычислить интеграл, интегрируя по частям, .

4. Вычислить интеграл .

5. Найти определенный интеграл по формуле Ньютона-Лейбница

.

1. Изобразить на плоскости область и изменить порядок интегрирования:

.

2. Вычислить двойной интеграл

3. Найти площадь фигуры, ограниченной данными линиями:

.

4. Вычислить объем тела, заданного ограничивающими его поверхностями:

.

5. Найти координаты центра масс однородных плоских фигур, ограниченных кривыми ,

1. Найти градиент скалярного поля

2. Найти производную функции в точке по направлению S

M₀(2; 1; 1) S = (-1; 2; 2)

3. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя)

,

, , ,

4. Найти циркуляцию векторного поля вдоль контура Г (в направлении, соответствующем возрастанию параметра t)

,

1. Найти общее решение дифференциального уравнения:

.

2. Найти общее решение дифференциального уравнения:

3. Решить задачу Коши для дифференциального уравнения:

.

4. Найти общее решение дифференциального уравнения:

5. Найти общее решение дифференциального уравнения:

.

ВАРИАНТ №6

1. Вычислить

2. Вычислить интеграл с помощью подстановки .

3. Вычислить интеграл, интегрируя по частям, .

4. Вычислить интеграл .

5. Найти определенный интеграл по формуле Ньютона-Лейбница

.

1. Изобразить на плоскости область и изменить порядок интегрирования:

.

2. Вычислить двойной интеграл

3. Найти площадь фигуры, ограниченной данными линиями:

.

4. Вычислить объем тела, заданного ограничивающими его поверхностями:

.

5. Найти координаты центра масс однородных плоских фигур, ограниченных кривыми ,

1. Найти градиент скалярного поля

2. Найти производную функции в точке по направлению S

M₀(2; 1; 1) S = (1; 2; 2)

3. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя)

,

, ,

4. Найти циркуляцию векторного поля вдоль контура Г (в направлении, соответствующем возрастанию параметра t)

,

1. Найти общее решение дифференциального уравнения:

.

2. Найти общее решение дифференциального уравнения:

3. Решить задачу Коши для дифференциального уравнения:

.

4. Найти общее решение дифференциального уравнения:

5. Найти общее решение дифференциального уравнения:

.

ВАРИАНТ №7

1. Вычислить

2. Вычислить интеграл с помощью подстановки .

3. Вычислить интеграл, интегрируя по частям, .

4. Вычислить интеграл .

5. Найти определенный интеграл по формуле Ньютона-Лейбница

.

1. Изобразить на плоскости область и изменить порядок интегрирования:

.

2. Вычислить двойной интеграл

3. Найти площадь фигуры, ограниченной данными линиями:

.

4. Вычислить объем тела, заданного ограничивающими его поверхностями:

.

5. Найти координаты центра масс однородных плоских фигур, ограниченных кривыми , ,

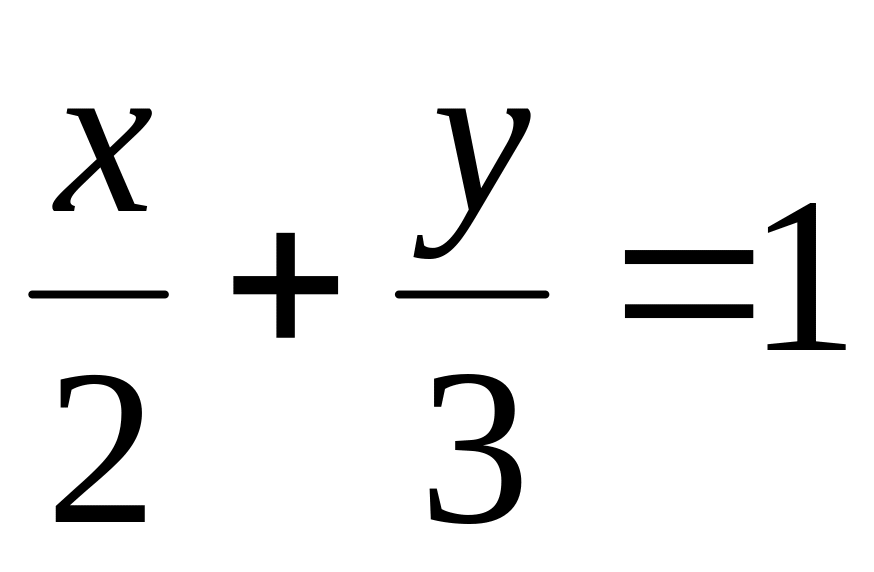1. Найти градиент скалярного поля

2. Найти производную функции в точке по направлению S

M₀(1; 1; 1) S = (2; 2; 1)

3. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя)

4. Найти циркуляцию векторного поля вдоль контура Г (в направлении, соответствующем возрастанию параметра t)

,

1. Найти общее решение дифференциального уравнения:

.

2. Найти общее решение дифференциального уравнения:

3. Решить задачу Коши для дифференциального уравнения:

.

4. Найти общее решение дифференциального уравнения:

5. Найти общее решение дифференциального уравнения:

.

ВАРИАНТ №8

1. Вычислить

2. Вычислить интеграл с помощью подстановки .

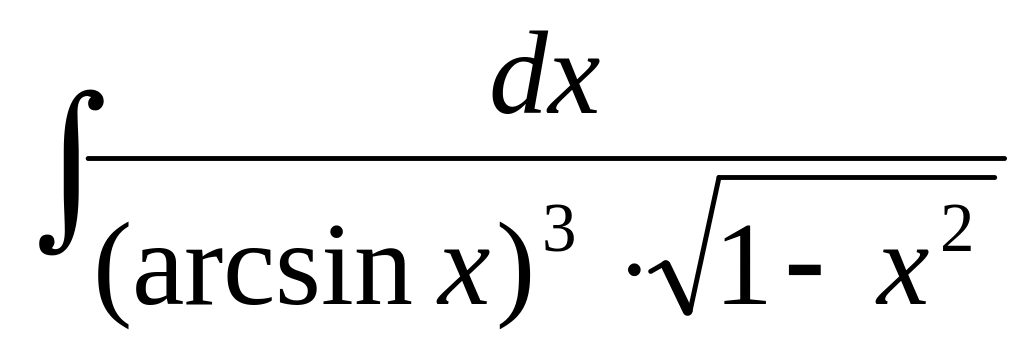3. Вычислить интеграл, интегрируя по частям, .

4. Вычислить интеграл .

5. Найти определенный интеграл по формуле Ньютона-Лейбница

.

1. Изобразить на плоскости область и изменить порядок интегрирования:

.

2. Вычислить двойной интеграл

3. Найти площадь фигуры, ограниченной данными линиями:

.

4. Вычислить объем тела, заданного ограничивающими его поверхностями:

.

5. Найти координаты центра масс однородных плоских фигур, ограниченных кривыми ,

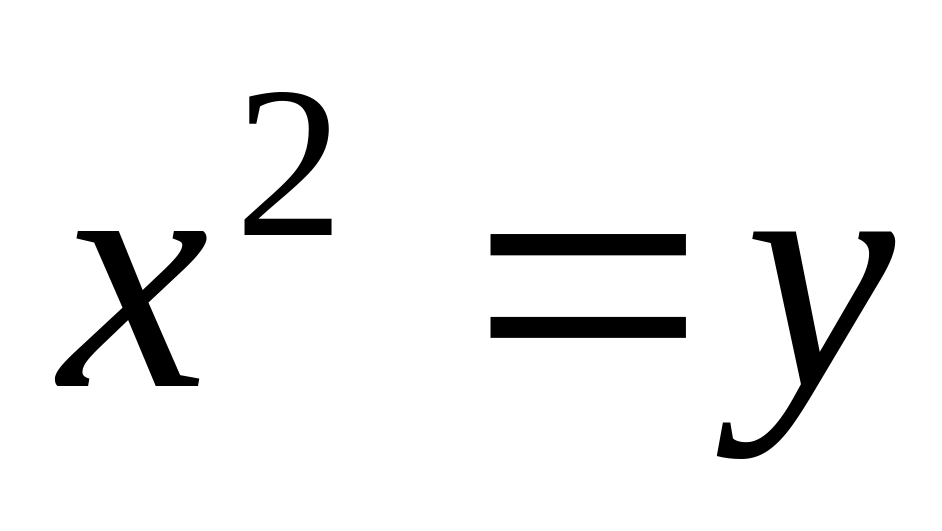
1. Найти градиент скалярного поля

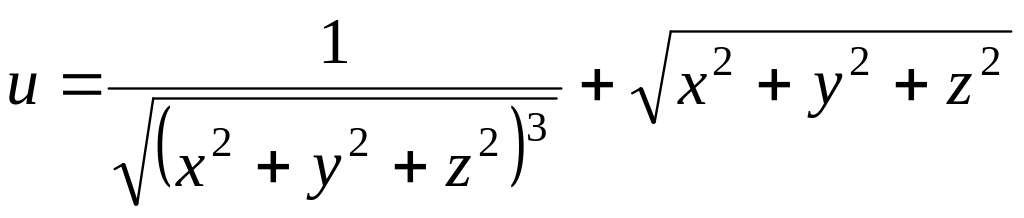
2. Найти производную функции в точке по направлению S

M₀(1; 1; 2) S = (2; 2; 1)

3. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя)

,

,

4. Найти циркуляцию векторного поля вдоль контура Г (в направлении, соответствующем возрастанию параметра t)

,

1. Найти общее решение дифференциального уравнения:

.

2. Найти общее решение дифференциального уравнения:

3. Решить задачу Коши для дифференциального уравнения:

.

4. Найти общее решение дифференциального уравнения:

5. Найти общее решение дифференциального уравнения:

.

ВАРИАНТ №9

1. Вычислить

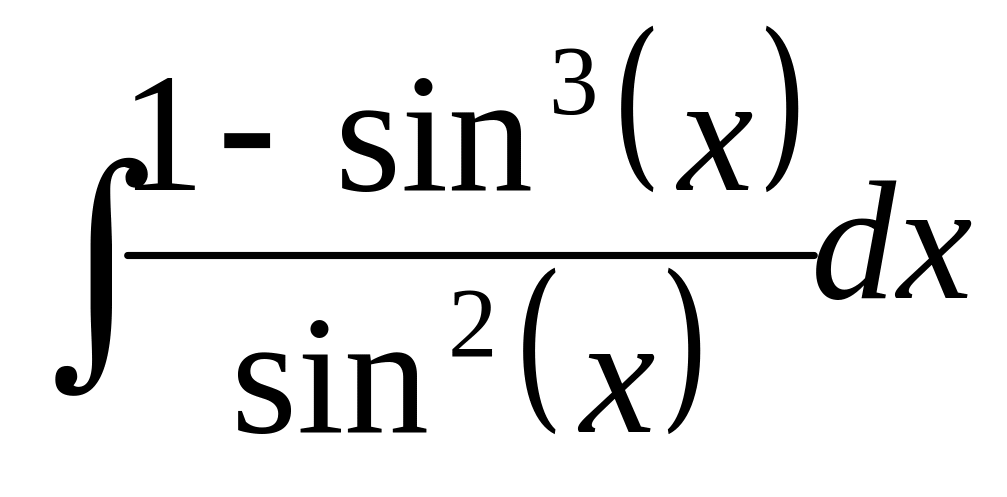
2. Вычислить интеграл с помощью подстановки .

3. Вычислить интеграл, интегрируя по частям, .

4. Вычислить интеграл .

5. Найти определенный интеграл по формуле Ньютона-Лейбница

.

1. Изобразить на плоскости область и изменить порядок интегрирования:

.

2. Вычислить двойной интеграл

3. Найти площадь фигуры, ограниченной данными линиями:

.

4. Вычислить объем тела, заданного ограничивающими его поверхностями:

.

5. Найти координаты центра масс однородных плоских фигур, ограниченных кривыми

,

1. Найти градиент скалярного поля

2. Найти производную функции в точке по направлению S

M₀(1; 0; 1) S = (2; 1; 1)

3. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя)

,

, , , .

4. Найти циркуляцию векторного поля вдоль контура Г (в направлении, соответствующем возрастанию параметра t)

1. Найти общее решение дифференциального уравнения:

.

2. Найти общее решение дифференциального уравнения

3. Решить задачу Коши для дифференциального уравнения:

.

4. Найти общее решение дифференциального уравнения:

5. Найти общее решение дифференциального уравнения

.

ВАРИАНТ №10

1. Вычислить

2. Вычислить интеграл с помощью подстановки .

3. Вычислить интеграл, интегрируя по частям, .

4. Вычислить интеграл .

5. Найти определенный интеграл по формуле Ньютона-Лейбница

.

1. Изобразить на плоскости область и изменить порядок интегрирования:

.

2. Вычислить двойной интеграл

3. Найти площадь фигуры, ограниченной данными линиями:

.

4. Вычислить объем тела, заданного ограничивающими его поверхностями:

.

5. Найти координаты центра масс однородных плоских фигур, ограниченных кривыми

,

1. Найти градиент скалярного поля

2. Найти производную функции в точке по направлению S

M₀(0; 1; 1)) S = (1; 2; 2)

3. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя)

,

4. Найти циркуляцию векторного поля вдоль контура Г (в направлении, соответствующем возрастанию параметра t)

,

1. Найти общее решение дифференциального уравнения:

.

2. Найти общее решение дифференциального уравнения

3. Решить задачу Коши для дифференциального уравнения:

.

4. Найти общее решение дифференциального уравнения:

5. Найти общее решение дифференциального уравнения

.