Методические указания по выполнению работы

1. Ознакомиться со схемой естественной термопары «резец-деталь» (рис. 3.1).

2. Ознакомиться с методом измерения температуры в зоне резания [5, 6, 8].

3. Измерить температуру в зоне резания при точении на различных скоростях V, подачах S , глубинах резания t. Данные опытов занести в таблицу (Приложение 3).

Для этого обрабатываемая заготовка устанавливается в патрон и поджимается вращающимся центром задней бабки. Заготовка и резец изолируются от станка. Резец и заготовка соединяются между собой через милливольтметр с использованием ртутного токосъёмника. Затем на указанных преподавателем режимах резания производится проточка заготовки с фиксацией ТЭДС. По тарировочному графику перевести показания милливольтметра (мВ) в градусы и занести в протокол опытов (см. бланк отчёта).

4. На основании полученных экспериментальных данных, используя графоаналитический метод обработки экспериментальных данных и метод наименьших квадратов, вывести зависимость температуры  от элементов режима резания, которая в общем виде может быть представлена степенной функцией

С₀ · V^z · s^у · t^x, C, (3.1)

где С₀ – коэффициент, зависящий от материалов заготовки и рабочей части резца, а также от условий резания;

V – скорость резания, м/мин;

s – подача, мм/об;

t – глубина резания, мм;

z, y, x – показатели степени, зависящие от материалов заготовки и резца, а также условий резания.

Обработка экспериментальных данных графоаналитическим методом

Формула (3.1) является общей, учитывающей одновременное влияние V, s, t. Частными формулами, определяющими зависимость температуры от каждого отдельно взятого элемента режима резания, будут:

_ C₀₁ · V^z; (3.2)

_ = C₀₂ · V^y; (3.3)

_ = C₀₃ · V^x . (3.4)

Обработка экспериментальных данных значительно упростится, если зависимости (3.2), (3.3), (3.4) построить в двойной логарифмической системе координат. Будучи прологарифмированы, уравнения (3.2), (3.3), (3.4) превращаются в уравнения первой степени и, следовательно, в двойной логарифмической системе координат изображаются прямыми линиями, тангенсы угла наклона которых равны показателям степени x, y, z (рис. 3.3).

Следовательно, построив на основании экспериментальных данных графики в двойных логарифмических координатах, можно определить показатели степени z, y, x, которые соответственно равны tg_, tg_{ ,} tg_.

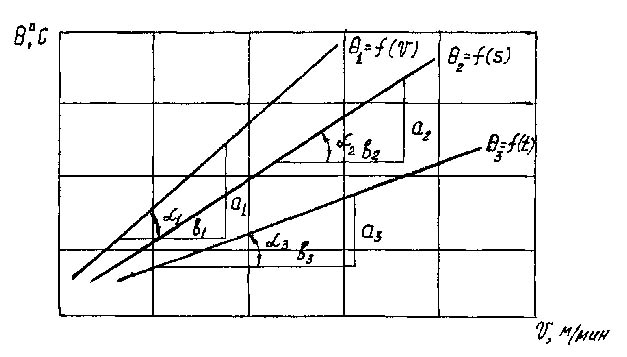
Рис. 3.3. Характерная зависимость от режимов резания V, м/мин; S, мм/об; t, мм

По известным величинам z, y, x значение С₀ рассчитывается по формуле

С₀ =  / V^z · s^y · t^x . (3.5)

Для этого из любой строки протокола опытов необходимо подставить значения  V, s, t в формулу (3.5) . Рассчитав три значения С_01, С_02, С₀₃ (для любых 3-х строк) и определив среднеарифметическое значение С₀, записать уравнение (3.1) в развернутом виде с указанием численных значений С_0ср, z, y, x.

Например,

 · V^0,52 · s^0,81 · t^0,05, C.