6. Анықтама туралы. Негізгі қасиеттер анықтамалар арқылы аталады, белгіленеді.

Расында математикалық сөйлемдерді қаз-қатар жаза беріп, анықтамасыз да жеткізуге болар еді. Бірақ анықтамалар тексті ықшамдап, маңызды жерлерін анық көрсетуге мүмкіндік береді. Белгілі бір мағынада осы кітаптың мазмұны негізгі ұғымдарды анықтып, олардың арасындағы байланысты зерттеу болады.

Анықтама қабылданады да, ешқашанда дәлелденбейді, бірақ кейбір жағдайларда оның қабылдану себептері түсіндірілуі, талқыланылуы мүмкін.

Бұл айтылғандарды халық тілімен ауыстырып, әрбір сөзді анықтама ретінде қарастыруға болады: сөз – белгі, ал ол нені белгілеп тұрғаны түсіндірме сөздікте берілген (әр халықтың өзінің түсіндірме сөздігі бар).

Тілдің маңызы туралы айтпаса да болады.

§ 2. Жиын мен функция ұғымдары

1. Жиындарға қолданылатын кейбір амалдар. Егер р әріпімен белгілі бір қасиетті белгілесек, онда сол қасиетті қабылдайтын заттардың бәрінен құрылған жиын

E={x : х заты P қасиетін қабылдайды} (1)

символымен белгіленеді.

Егер Р қасиетін бірде-бір зат қабылдамаса, онда (1) жиынын бос жиын дейді де,  символымен белгілейді.

Мысалы, E={x: x – нақты сан, x²+1=0 }= (мұнда P қасиеті ретінде х заты нақты сан болып, оның квадраты мен 1 санының қосындысы 0-ге тең болуы алынған).

Енді жиындарға қолданылатын кейбір амалдарды анықтайық.

1. Жиындардың теңдігі. Жоғарыда анықталған  кірістіру символы бойынша жиындардың теңдігі анықталады.

Егер Е және F жиындары үшін EF және FE кірістірулері бірдей орындалса, яғни бірінің кез келген элементі екіншісіндежатса, онда Е және F жиындары тең дейді де, E=Fсимволымен белгілейді.

Т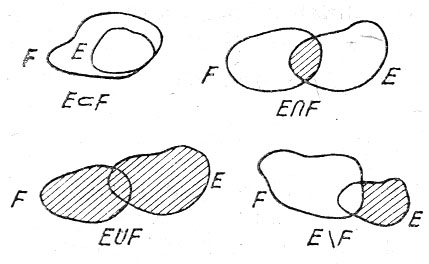 өменгі анықтамаларда = таңбасының сол жағындағы символдар оң жағындағы жиындардың белгілеулері болады.

Сурет-1

2. Жиындардың қиылысуы. Е және F жиындарының қиылысуы деп ЕF={x : xE және xF } жиынын, яғни Е мен F жиындарынды бірдей жататын х элементтерінен құрылған жиын аталады. Егер ондай элементтер болмаса, онда ЕF =.

3. Жиындардың бірігуі. Е және F жиындардың біріктірілуі деп ЕF={x: xE немесе xF} жиынын, яғни Е және F жиындарының кемінде біреуінде жатқан элементтерінен құрылған жиынды атайды (бұған Е мен F-те қатар жататын элементтер де кіреді).

4. Жиындардың айырымы. Е және F жиындарының айырымы деп E—F={x: xE және x F жиыны, яғни Е жиынында жатып, F жиынында жатпайтын х элементтерінің жиыны аталады.

Әрине, EF; EF болған жағдайда (F—E) жиын болады.

E мен F жазықтықтың жиыншалары болғанда, жоғарыда келтірілген анықтамалар 1-суретте бейнеленген:

2. Функция ұғымы. Е және F жиындары берілсін. Е жиынының әрбір элементіне F жиынының элементін сәйкес қоятын ереже функция деп аталады. Бұл ережені тәртіп, заң, амал, сәйкестік, тәуелділік деп те атайды.

Жиындардың элементтерін белгілеу үшін символдар қолданылады. Е жиынының кез келген элементін бейнелейтін символ тәуелсіз айнымалы немесе функцияның аргументі деп аталады. Осыған орай, тәуелсіз айнымалыға немесе аргументке сәйкес элементті белгілейтін символ тәуелді айнымалы деп аталады. Бұл символдарды қандай етіп таңдап алуымызға ешқандай шарт қойылмайды. Мысалы,  фигурасын немесе ұ, ң, қ әріптерін де қолдануға болады.

Бірақ, көбінесе айнымалыны латын (мысалы, x,y,z,t,u,v,…) және грек (мысалы, ,,,,,, ...) әріптерімен белгілеу ертеден қалыптасып кеткен. Функцияның анықтамасындағы ереже көбінесе f,,,, ... әріптерімен белгіленеді.

f(x) символын «х элементіне f, ережесі қолданылған» деген сөйлемшенің қысқаша жазылуы деп түсіну керек. f(x)F элементі f функциясының хЕ нүктесінде қабылданған мәні деп аталады. Сонымен, y_оF элементі f функциясының мәні болады деген сөз белгілі бір х_оЕ үшін у_о=f(х_о) теңдігі орындалуымен пара-пар.

Функция көбінесе ; f: ; x f(x); f(x); y= f(x); f: хЕ, f(x)F символдарымен белгіленеді.

Әрине, бұл әріптермен белгілеулердің қайсысын қолданғанымыз – бәрі бір. Мысалы, f(x)=x², f(y)=y², ² немесе хх², ², х=², ух=y² жазуларының бәрі де әрбір нақты санға квадратын сәйкес қоятын ережені бейнелейді.

Е – функцияның анықталу жиыны, ал F – функцияның мәндері қабылдайтын жиын деп аталады.

Функцияның анықтамасында келесі үш ұғымды бөлген жөн: