Инструкция к практической работе № 3. Решение алгебраических и трансцендентных уравнений с помощью инструментальных средств (ms Excel)
Отделение корней уравнения аналитическим способом
Чтобы отделить корни уравнения аналитическим способом с помощью MS Excel, необходимо выполнить следующее:
Заполнить ячейки A1:D1 соответственно: «x», «y=cos(2x)+x-5», «h», «ответ».
В С2 ввести значение 1.
Ввести в А2 значение -10.
Ввести в А3 =СУММ(A2;$C$2), выделить А3 и методом протягивания заполнить ячейки А4:А22.
В В2 ввести =COS(2*A2)+A2-5 и методом протягивания заполнить диапазон В3:В22.
В С3 ввести формулу =ЕСЛИ(B2*B3<0;"Корень на отрезке существует";ЕСЛИ(B3=0;"точный корень";"-")) и методом протягивания заполнить диапазон ячеек С4:С22.
В результате получаем следующее:
Рассмотрим полученный отрезок изоляции [5;6].
Для доказательства существования корня на отрезке изоляции необходимо выполнить следующие действия:
Запустить MS Excel.
Ввести в ячейки А1, В1 и С1 соответственно «x», «y=cos(2x)+x-5» и «ответ».
В А2 и А3 ввести граничные значения отрезка изоляции.
В В2 ввести формулу =COS(2*A2)+A2-5 и методом протягивания заполнить В3.
В С2 ввести формулу =ЕСЛИ(B2*B3<0;"корень существует";"корень не существует").
Таким образом, на отрезке изоляции корень существует:
Для доказательства единственности корня на отрезке изоляции необходимо выполнить следующие действия:
Продолжить работу в том же документе MS Excel.
Заполнить D1 и E1 соответственно: «y'=-sin(2x)*2+1» и «ответ» (причем выражение y'=-sin(2x)*2+1 – это производная первого порядка от функции y=cos(2x)+x-5).
Ввести в D2 формулу =-SIN(2*A2)*2+1 и методом протягивания заполнить D3.
Ввести в E2 =ЕСЛИ(D2*D3>0;"корень на данном отрезке единственный";"Корень не единственный").
В результате получаем:
Таким образом, доказано существование и единственность корня на отрезке изоляции.
Графический способ отделения корней уравнения
1 Способ
Построим график функции f(x)=cos(2x)+x-5 в декартовой системе координат.
Для этого нужно:
Ввести в ячейку A1 текст х.
В
вести
в ячейку B1 текст y=cos(2x)+x-5.Ввести в ячейку А2 число -10, а в ячейку А3 число -9.
Выделить ячейки А2 и А3.
Навести указатель «мыши» на маркер заполнения в правом нижнем углу рамки, охватывающий выделенный диапазон. Нажать левую кнопку «мыши» и перетащить маркер так, чтобы рамка охватила диапазон ячеек А2:А22.
Ячейки автоматически заполняются цифрами:
Ввести в ячейку В2 формулу =COS(2*A2)+A2-5.
Методом протягивания заполнить диапазон ячеек В3:В22.
Вызвать "Мастер диаграмм" и выбрать диаграмму график (первый вид), нажать «далее».
Указать диапазон данных, для этого щелкнуть кнопку в поле «Диапазон» и выбрать диапазон данных В2:В22.
Выбрать вкладку ряд, указать имя ряда, щелкнув кнопку в поле «ряд» и выбрав В1.
В поле «подписи по оси Х», щелкнуть кнопку и выбрать диапазон А2:А22, нажать «далее».
Подписать названия осей x и y соответственно, нажать «далее».
Вывести диаграмму на том же листе, что и таблица, нажать кнопку «готово».
В итоге получаем следующее:
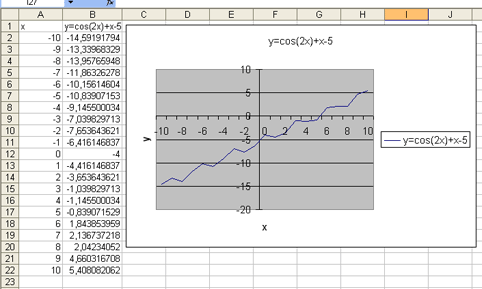
Анализируя полученное изображение графика, можно сказать, что уравнение cos(2x)+x-5=0 имеет один корень – это видно из пересечения графика функции y=cos(2x)+x-5 с осью OX. Можно выбрать отрезок, содержащий данный корень: [5;6] – отрезок изоляции.