7.2 Расчётно-проектировочная работа № 6 «Расчёты на устойчивость продольно сжатых стержней»

Пример 22. Для стойки из четырех уголков № 7,5/5,0×0,5 и четырех пластин размерами 20х1,0 см, жёстко защемлённой нижним концом, из расчёта на устойчивость определить допускаемую сжимающую нагрузку и коэффициент запаса устойчивости Материал конструкционная сталь марки Ст.3, модуль номаль

ной упругости , допускаемое напряжение на сжатие , предел пропорциональности . Длина стойки . Концы стойки имеют одинаковый способ их закрепления в обоих главных плоскостях сечения, в соответствии с рисунком 7.4

Ход решения.

1. Определяем геометрическую гибкость стойки

,

где - коэффициент приведения длины стойки, жёстко защемлённой одним концом;

n = 0,5 – число полуволн синусоиды изогнутой оси стойки, потерявшей устойчивость;

- минимальный радиус инерции сечения в плоскости с минимальной жесткостью стойки при изгибе, в которой происходит потеря устойчивости. Определение геометрических характеристик сечения рассмотрено в примере 2

2. Определяем предельную гибкость для Ст3

,

3. Определяем критическую силу и критическое напряжение. При геометрической гибкости стойки для их расчёта принимаются формулы Л.Эйлера

МПа

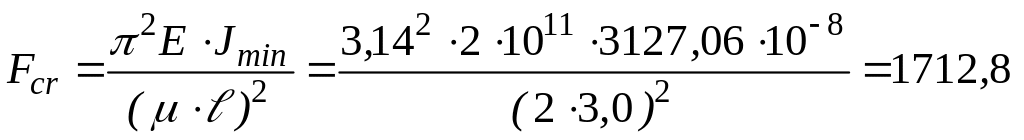кН

4. Определяем коэффициент снижения основного допускаемого напряжения на сжатие для Ст.3 при . По таблице коэффициента находим

Действительное значение

5. Из условия устойчивости определяем допускаемую нагрузку кН

6. Определяем коэффициент запаса устойчивости

1712,8/755,3 =2,26, что в пределах допускаемой величины

Примечания: 1. Если геометрическая гибкость будет больше табличной величины, то расчётную длину стойки в дальнейших расчётах уменьшить так, чтобы .

2. Если геометрическая гибкость , то критическое напряжение определяется по формуле Ясинского , а , где а = 311 МПа, b = 11,4 МПа – коэффициенты для Ст 3.

Если , то МПа,

Пример 23. Для стойки длиной м, нагруженной сжимающей силой F₁ = 200 кН, из расчёта на устойчивость определить размеры прямоугольного поперечного сечения при h =2b. Материал конструкционная сталь марки Ст3, основное допускаемое напряжение на сжатие МПа. Способ закрепления концов стойки в обоих главных плоскостях считать одинаковым, в соответствии с рисунком 7.5.

Ход решения

1.Записываем условие устойчивости или Так как в условии устойчивости имеется два неизвестных, то задача решается методом последовательного приближения, при котором задаются одним из неизвестных. В данном варианте . Поэтому выгодно задаваться его величиной.

В первом приближении задаёмся . Тогда из условия устойчивости в первом приближении

.

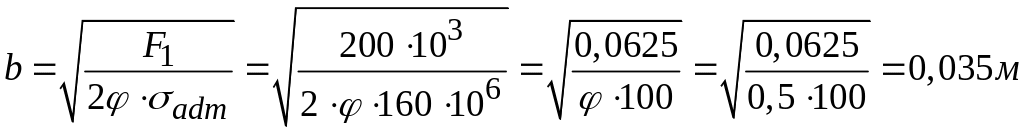м.

3. Для полученных размеров определяем геометрическую гибкость стержня

где - коэффициент приведения длины стойки с шарнирно подвижной верхней и жестко защемленной нижней опорами;

- минимальный радиус инерции сечения.

4. Определяем коэффициент снижения основного допускаемого напряжения на сжатие для стойки из Ст.3 при . По таблице находим

Действительное значение

Коэффициент заданный и действительный тождественно не равны.

5. Во втором приближении задаётся Тогда м, м.

Коэффициент снижения основного допускаемого напряжения для стойки из Ст.3 при .

Действительное значение

Коэффициент заданный и действительный тождественно не равны.

6. В третьем приближении задаёмся

Тогда 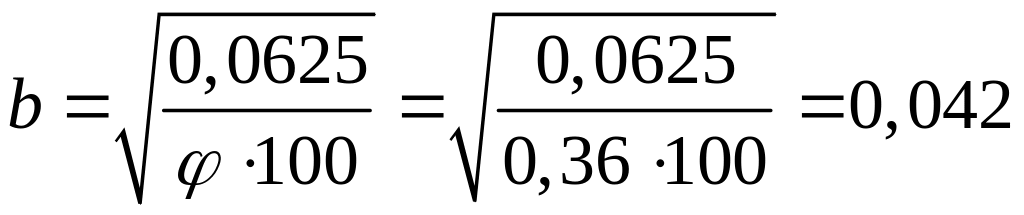м, м,

Коэффициент снижения основного допускаемого напряжения

Действительное значение

Коэффициенты заданный и действительный практически равны.

Для проверки правильности расчётов из условия устойчивости определяем допускаемую сжимающую нагрузку.

кН, что больше заданной силы на . Это меньше точности расчётов ±5%.