
- •Обозначения и основные символы
- •Содержание
- •Предисловие
- •1.1 Основные положения
- •1.2 Вопросы и ответы для самоконтроля
- •2. Геометрические характеристики плоских сечений
- •2.1 Основные понятия и формулы
- •2.2 Расчетно-проектировочная работа № 1 «Геометрические характеристики плоских сечений»
- •2.3 Вопросы и ответы для самоконтроля
- •3 Внутренние силовые факторы
- •3.1 Основные понятия и формулы
- •3.2 Расчётно-проектировочная работа № 2 «Построение эпюр внутренних силовых факторов»
- •Ход решения
- •Ход решения
- •3.4. Вопросы и ответы для самоконтроля
- •4. Простые состояния стержней
- •4. 1 Состояние растяжения - сжатия. Основные понятия
- •Расчётно-проектировочная работа № 3. «Расчёты на прочность и жёсткость при простых состояниях стержней»
- •4.3 Вопросы и ответы для самоконтроля
- •4.4 Состояние кручения валов круглого сечения. Основные понятия и формулы.
- •4.5 Вопросы и ответы для самоконтроля
- •4.6 Состояние чистого изгиба. Основные понятия и формулы
- •4.7 Состояние поперечного изгиба. Основные понятия и формулы.
- •2. Строим эпюры внутренних силовых факторов
- •5. Производим подбор сечения
- •2. Строим эпюры поперечной силы и изгибающего момента
- •4.8 Вопросы и ответы для самоконтроля
- •5 Сложное сопротивление
- •5.1 Основные понятия и формулы
- •5.2 Косой изгиб. Основные понятия и формулы.
- •Расчетно-проектировочная работа № 4 « Расчеты на прочность при сложном сопротивлении»
- •5.4 Вопросы и ответы для самоконтроля
- •Внецентренное растяжение-сжатие. Основные понятия и формулы.
- •5.6 Вопросы и ответы для самоконтроля
- •5.7 Совместный изгиб с кручением. Основные понятия и формулы.
- •5.8 Вопросы и ответы для самоконтроля
- •6 Определение перемещений энергетическими методами.
- •6.1 Основные понятия и формулы
- •6.2 Расчётно-проектировочная работа № 5 «Определение перемещений при изгибе и решение статически неопределимой задачи»
- •6.3 Вопросы и ответы для самоконтроля
- •7 Устойчивость продольно сжатых стержней
- •7.1 Основные понятия и формулы
- •7.2 Расчётно-проектировочная работа № 6 «Расчёты на устойчивость продольно сжатых стержней»
- •7. 3 Вопросы и ответы для самоконтроля
- •8. Переменные напряжения
- •8.1 Основные понятия и формулы.
- •8.2 Расчётно-проектировочная работа № 7 «Проверочный расчёт вала по условиям усталостной прочности»
- •8.3 Вопросы и ответы для самоконтроля
- •Литература
- •Приложения
- •Сортамент прокатной стали
6.2 Расчётно-проектировочная работа № 5 «Определение перемещений при изгибе и решение статически неопределимой задачи»
Пример № 20. Для балки, нагруженной
внешними нагрузками
![]() кН,
кН,
![]() и
и
![]() кН/м, определить прогиб и угол
поворота сечения D.
Длина участков
кН/м, определить прогиб и угол
поворота сечения D.
Длина участков
![]() = 0,4 м, b = 1,2 м, с =
0,8 м, в соответствии с рисунком 6.2 а
= 0,4 м, b = 1,2 м, с =
0,8 м, в соответствии с рисунком 6.2 а
Ход решения
1. Определяем реакции опор от действия внешних нагрузок.
![]() .
Отсюда
.
Отсюда
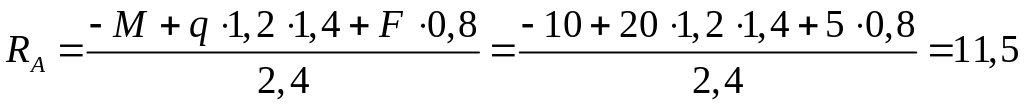 кН
кН
![]() .
Отсюда
.
Отсюда

Рисунок 6.2
 кН
кН
Проверка
![]()
2. Строим эпюры поперечной силы
![]() - и изгибающего момента
- от действия внешних нагрузок.
- и изгибающего момента
- от действия внешних нагрузок.
Для участка АВ
![]()
![]() кН
– Const.
кН
– Const.
![]()
![]() -
уравнение прямой
-
уравнение прямой 
Для участка BD
![]() -
уравнение прямой
-
уравнение прямой 
![]() -
уравнение квадратной параболы.
-
уравнение квадратной параболы. 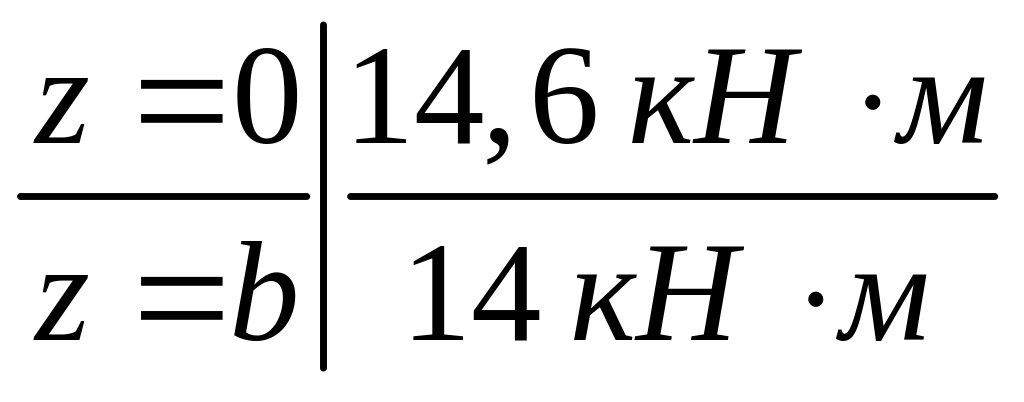
Определяем экстремальное значение изгибающего момента
![]() Отсюда
Отсюда
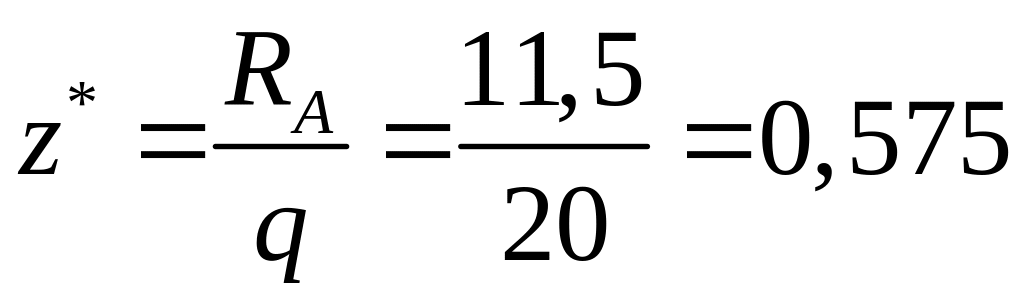 м
м
![]() ,
выпуклость эпюры изгибающего момента
,
выпуклость эпюры изгибающего момента
![]() вверх.
вверх.
Для![]() участка СD
участка СD
![]() кН - Const
кН - Const
![]()
![]() - уравнение прямой
- уравнение прямой

По найденным значениям строим эпюры поперечной силы и изгибающего момента от действия внешних нагрузок, в соответствии с рисунком 6.2 б.
3. Определяем опасное сечение по
максимальному изгибающему моменту.
Опасное сечение при
![]() м
с
м
с
![]() .
.
4. Составляем условие прочности

Определяем из условия прочности осевой момент сопротивления
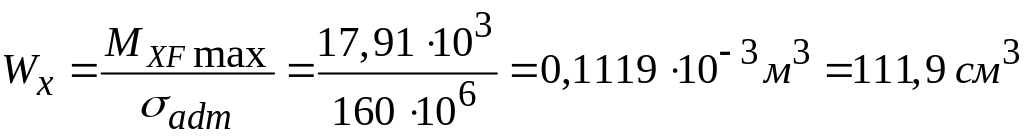
По
сортаменту подбираем двутавр № 16 с
![]() и
и
![]() .
Проверка
.
Проверка
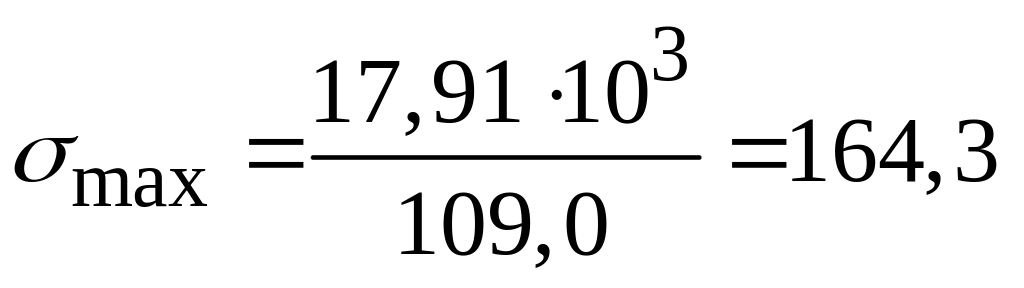 МПа,
что больше
МПа
на 2,68 %.
МПа,
что больше
МПа
на 2,68 %.
Это меньше 5 %.
5. Определяем прогиб сечения D.
а) Для этого составляем расчётную схему балки без внешних нагрузок и прикладываем в точке D единичную сосредоточенную силу F0 = 1 в направлении предполагаемого прогиба, в соответствии с рисунком 6.2 в.
б) Определяем реакции опор от действия F0 = 1.
![]() .
Отсюда
.
Отсюда
![]()
![]() .
Отсюда
.
Отсюда
![]()
Проверка
![]()
в) Составляем уравнения изгибающих
моментов от действия единичной силы
![]() по соответствующим участкам.
по соответствующим участкам.
Для
участка АВ
![]()
Для
участка ВD
![]()
Для
участка СD
![]()
г) Составляем уравнение интеграла Максвелла-Мора для определения прогиба.
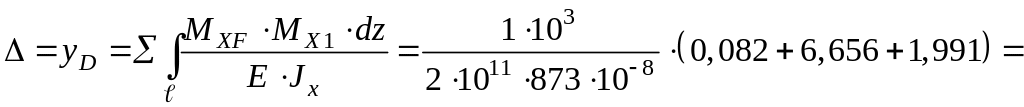
![]() м
= 5,0 мм, что меньше допускаемого
прогиба
м
= 5,0 мм, что меньше допускаемого
прогиба
![]()
![]() мм,
где
мм,
где
![]() - пролет балки.
- пролет балки.
Вывод: жёсткость балки обеспечена.
Для упрощения расчётов интегралы берутся по участкам
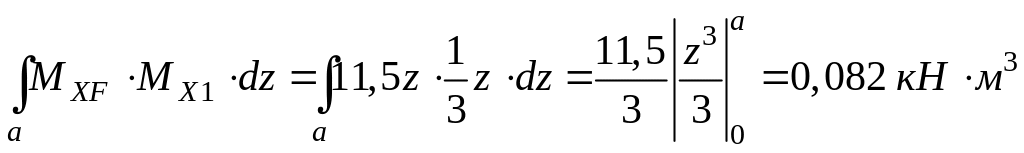 ,
,
 ,
,
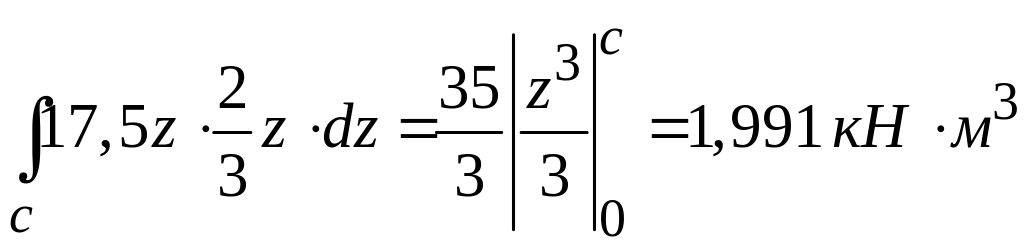 .
.
6. Определяем угол поворота сечения D
а) Для этого к расчётной схеме балки прикладываем в сечении D единичный сосредоточенный момент М0 = 1 в направлении предполагаемого угла поворота сечения D, в соответствии с рисунком 6.2 г
б) Определяем реакции опор от действия М0 = 1
![]() Отсюда
Отсюда
![]()
![]()
![]() Отсюда
Отсюда
![]()
Проверка
![]()
в) Составляем уравнения изгибающих
моментов от действия единичного момента
![]() по соответствующим участкам.
по соответствующим участкам.
Для участка АВ
![]() ,
,
для участка ВD
![]() ,
,
для участка СD
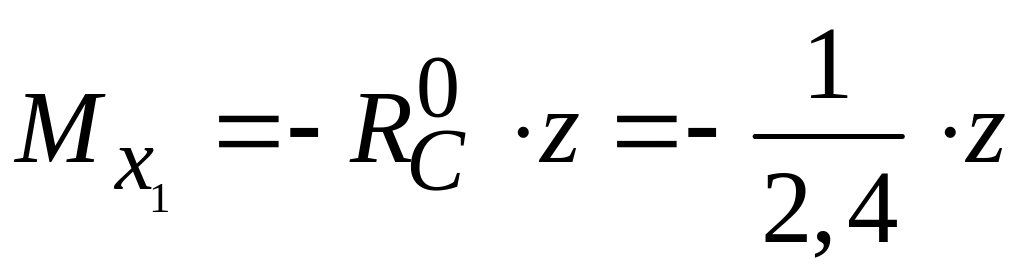 .
.
г) Составляем уравнение интеграла Максвелла-Мора для определения угла поворота сечения D

![]() ,
,
где
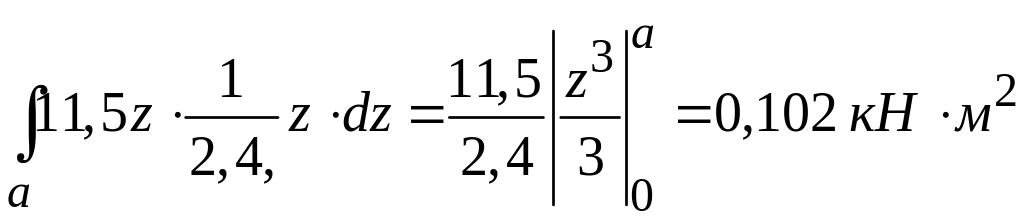 ,
,
 ,
,
 .
.
Знаки плюс в ответах показывают, что направления прогиба и угла поворота сечения D предположены верно.
Пример 21. Для статически неопределимой
балки, нагруженной внешними нагрузками
F = 5 кН,
![]() и q = 20 кН/м,
раскрыть статическую неопределимость,
построить эпюры внутренних силовых
факторов и подобрать сечение двутавра.
Длина участка b = 1,2
м, в соответствии с рисунком 6.3 а.
и q = 20 кН/м,
раскрыть статическую неопределимость,
построить эпюры внутренних силовых
факторов и подобрать сечение двутавра.
Длина участка b = 1,2
м, в соответствии с рисунком 6.3 а.
Ход решения.
1.Составляем уравнения равновесия статики.
![]() Отсюда
Отсюда
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
2. Определяем степень статистической неопределимости
![]() -
система один раз статически неопределима,
-
система один раз статически неопределима,
где
![]() -
число неизвестных реакций опор;
-
число неизвестных реакций опор;
![]() - число уравнений равновесия статики.
- число уравнений равновесия статики.
3. Составляем основную систему в соответствии с рисунком 6.2 б.
Для этого в статически неопределимой
балке отбрасываем опору D
с «лишней» реакцией
![]()
4. Составляем эквивалентную систему в соответствии с рисунком 6.2 в.
Для этого к основной системе в сечении
D прикладываем «лишнюю»
реакцию
![]() без опоры D
без опоры D
5. Составляем каноническое уравнение
метода сил: перемещение (прогиб) сечения
D в направлении лишней реакции
равно нулю
![]()
6. Строим эпюры изгибающих моментов от действия внешних нагрузок, приложенных к эквивалентной системе, по методу расслоения эпюр (принцип независимости действия сил), в соответствии с рисунками 6.3 г, д, е.
7. Строим эпюру изгибающего момента от единичной сосредоточенной силы Х10 = 1, приложенной к эквивалентной системе в направлении «лишней» реакции , в соответствии с рисунком 6.3 ж.
8. Определяем коэффициенты канонического
уравнения по формуле Верещагина

где
![]() - площади эпюр изгибающих моментов от
внешних и единичной нагрузок по участкам;
- площади эпюр изгибающих моментов от
внешних и единичной нагрузок по участкам;
![]() -
ординаты эпюр изгибающего момента от
единичной силы Х10 = 1,
взятые под центром тяжести эпюр
изгибающего момента от внешних и
единичных нагрузок;
-
ординаты эпюр изгибающего момента от
единичной силы Х10 = 1,
взятые под центром тяжести эпюр
изгибающего момента от внешних и
единичных нагрузок;
- жёсткость балки при изгибе.
![]()
![]() -
перемещение точки приложения ''лишней''
реакции
в направлении её действия от действия
внешних нагрузок;
-
перемещение точки приложения ''лишней''
реакции
в направлении её действия от действия
внешних нагрузок;
![]() м3 - перемещение точки
приложения лишней реакции Х1
от единичной силы
м3 - перемещение точки
приложения лишней реакции Х1
от единичной силы
![]() =
1 в направлении действия «лишней»
реакции
=
1 в направлении действия «лишней»
реакции
![]()
Получаем
![]() Отсюда
Отсюда
![]() кН
кН
9. Определяем оставшиеся реакции опор из уравнений равновесия статики.
Из
(3)
![]() 11,36
кН
11,36
кН
Из
(2)
![]() кН
кН
Знаки плюс у всех реакций показывают, что их направление выбрано верно.
Проверка.
![]()
![]() .
.
10. Строим эпюры поперечной силы и изгибающего момента для статически неопределимой системы.
Для
участка АВ
![]() - уравнение прямой
- уравнение прямой ![]()
![]() - уравнение квадратной параболы
- уравнение квадратной параболы ![]()

Рисунок 6.3
Определяем
экстремальное значение МХ
![]() Отсюда
Отсюда
![]() м
м
![]()
, выпуклость эпюры МХ вверх.
Для участка DC
![]()
![]() кН
– Const.
кН
– Const.
![]() -
уравнении е прямой
-
уравнении е прямой ![]()
Для участка СВ
![]()
![]()
![]() кН – Const.
кН – Const.
![]() - уравнение прямой
- уравнение прямой ![]()
![]()
По найденным значениям строим эпюры поперечной силы и изгибающего момента, в соответствии с рисунком 6.3 з.
11. Определяем опасное сечение по
максимальному изгибающему моменту.
Опасное сечение D с
![]() .
.
12. Из условия прочности
![]() определяем осевой момент сопротивления
определяем осевой момент сопротивления
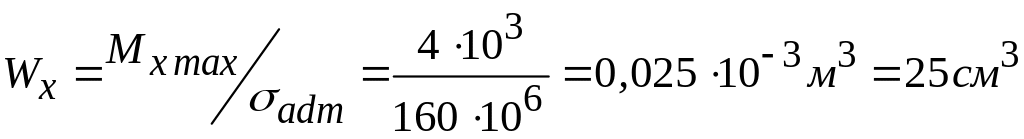
По сортаменту подбирается только швеллер
№ 10 с
![]() ,
что на 39,6% больше требуемой величины.
,
что на 39,6% больше требуемой величины.
