5.8 Вопросы и ответы для самоконтроля

1. Какое состояние стержня называется совместным косым изгибом с кручением ?

Состояние стержня, при котором в его сечениях действуют поперечные силы , , изгибающие моменты , и крутящий момент , называется совместным изгибом с кручением.

2. Чему равен результирующий изгибающий момент ?

Результирующий изгибающий момент равен геометрической сумме изгибающих моментов , . Его величина .

3. Формула для определения результирующих нормальных напряжений от результирующего изгибающего момента.

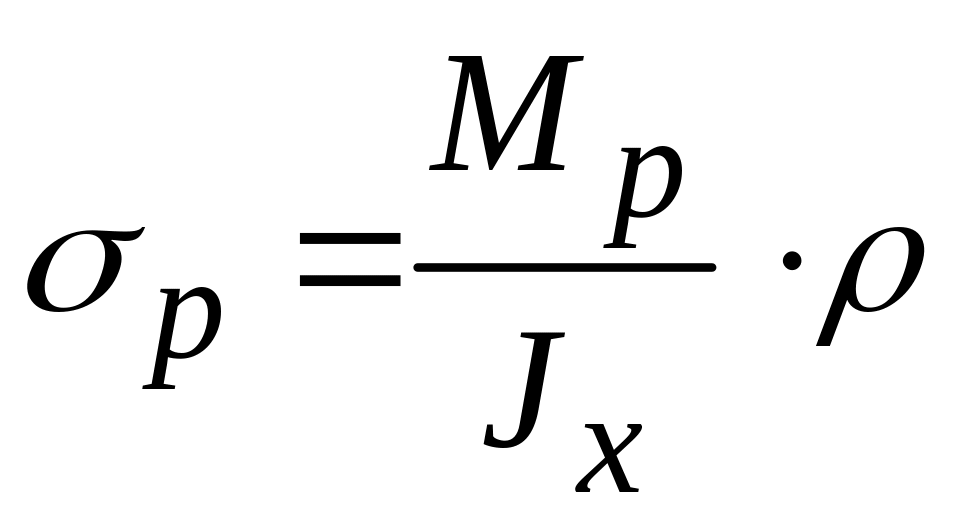Результирующие нормальные напряжения прямо пропорциональны результирующему изгибающему моменту и расстоянию от нейтральной линии до исследуемой точки сечения и обратно пропорциональны осевому моменту инерции сечения относительно нейтральной линии.

4. Закон распределения результирующих нормальных напряжений по сечению при совместном изгибе с кручением.

Результирующие нормальные напряжения по сечению распределяются в плоскости его действия по закону прямой от нуля в нейтральном слое до максимальной величины в точках поверхностного слоя.

5. Формула для определения максимального результирующего нормального напряжения.

Максимальное результирующее нормальное напряжение прямо пропорционально результирующему изгибающему моменту и обратно пропорционально осевому моменту сопротивления относительно нейтрального слоя.

6. Формула для определения касательных напряжений от крутящего момента.

Касательные напряжения прямо пропорциональны крутящему моменту и расстоянию от оси кручения до исследуемой точки сечения и обратно пропорциональны полярному моменту инерции сечения.

7.Закон распределения касательных напряжений от по сечению.

Касательные напряжения по сечению распределяются по закону прямой от нуля на оси кручения до максимальной величины в точках поверхностного слоя.

8. Формула для определения максимального касательного напряжения.

Максимальное касательное напряжение прямо пропорционально крутящему моменту и обратно пропорционально полярному моменту сопротивления сечения.

9. Условие прочности при совместном изгибе с кручением.

Максимальное эквивалентное напряжение прямо пропорционально расчетному моменту и обратно пропорционально осевому моменту сопротивления сечения и не должно превышать величины допускаемого нормального напряжения.

10. Решение задач по условию прочности.

Проектировочная задача определения размеров сечения

Проверочная задача определения допускаемого расчетного момента

Проверочная задача проверки прочности и определения коэффициента запаса прочности .

11. Формулы для определения расчетных моментов.

- расчетный момент по III теории прочности;

- расчетный момент по IV теории прочности.

6 Определение перемещений энергетическими методами.

6.1 Основные понятия и формулы

При изгибе продольная ось балки изгибается в пределах упругих деформаций. Изогнутая ось балки в пределах упругих деформаций называется упругой линией или линий прогибов и описывается приближенным дифференциальным уравнением изогнутой оси балки . Перемещение центра тяжести сечения перпендикулярно первоначальному положению оси балки называется прогибом сечения. Рисунок 6.1

Рисунок 6.1

Поворот поперечного сечения относительно первоначального положения называется углом поворота сечения. Зависимость между углом поворота и прогибом сечения выражается дифференциальным уравнением . Угол

поворота в любом сечении равен производной от уравнения изогнутой оси балки в этом сечении. Для балок с постоянной жесткостью

.

Кривизна изогнутой оси балки выпуклостью вверх на участках с отрицательной эпюрой изгибающего момента и выпуклостью вниз на участках с положительной эпюрой изгибающего момента. Интегрируя дифференциальное уравнение изогнутой оси балки по всем участкам балки получаем

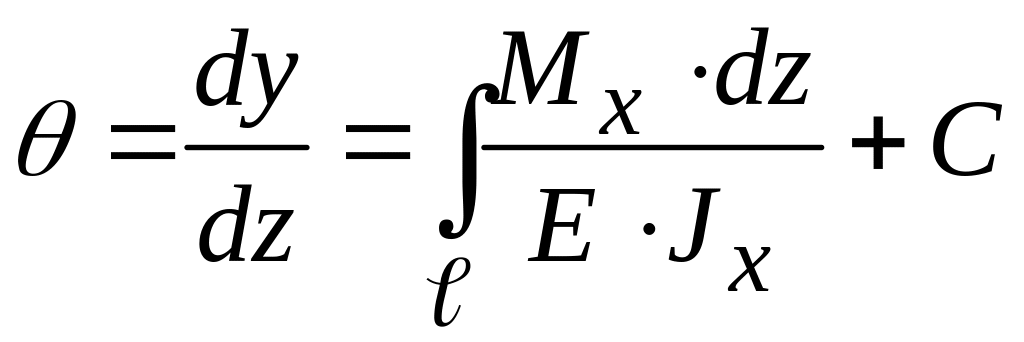- уравнение углов поворота сечений;

- уравнение прогибов сечений,

где С, D - постоянные интегрирования, численно равные углу поворота и прогибу сечения балки в начале принятой неподвижной системы координат, увеличенные в раз.

Определение прогиба и угла поворота сечений балок и рам, пренебрегая действием продольной и поперечной сил, проводится по формуле интеграла Максвелла – Мора .

где - уравнения изгибающего момента от действующих на балку внешних нагрузок по участкам;

- уравнения изгибающих моментов от единичной обобщенной нагрузки по соответствующим участкам.

Графическое интегрирование формулы Максвелла-Мора дает формулу Верещагина для определения перемещений при изгибе

Рисунок 6.2

Условие жесткости при изгибе записывается формулой

Допускаемый прогиб:

- для валов и шпинделей металлорежущих станков;

- для балок строительных конструкций

где - пролет балок между опорами.

Для определения усилий в статически неопределимых системах применяется метод сил. По этому методу заданная статически неопределимая система освобождается от «лишних» связей, а их действие заменяется реактивными силами или моментами. Их величина подбирается так, чтобы перемещения системы в направлении их действия соответствовали ограничениям, которые накладываются на систему отброшенными связями. Для раскрытия статической неопределимости балок при изгибе для эквивалентной системы составляются дополнительно уравнения совместности перемещений по числу «лишних» реакций, которые называются каноническими уравнениями метода сил.

Перемещение точки приложения любой «лишней» реакции в направлении ее действия от действия всех «лишних» реакций и системы внешних сил равно нулю.

- где - перемещение точки приложения «лишней» реакции в направлении ее действия от действия единичной обобщенной силы ;

- перемещение точки приложения «лишней» реакции в направлении ее действия от действия единичной обобщенной силы ;

- перемещения точек приложения «лишних» реакций в направлении их действия от действия системы внешних нагрузок.