Внецентренное растяжение-сжатие. Основные понятия и формулы.
Состояние стержня, при котором в его сечениях действуют продольная сила и изгибающие моменты , , называется внецентренным растяжением – сжатием. Рисунок 5.5а
Рисунок 5.5
При
этом
,
и
по длине стержня величины постоянные,
в соответствии с рисунком 5.5 б.
В сечениях стержня будут действовать
только результирующие нормальные
напряжения
,
которые по сечению распределяются по
закону прямой от нуля в нейтральном
слое до максимальной величины в наиболее
удаленных точках поверхностных слоев
сечения, в соответствии с рисунком 5.5
в.
Условие прочности по любой теории прочности
Для сечений, имеющих хотя бы одну ось симметрии
Уравнение
нейтральной линии
- уравнение прямой, не проходящей через
центр тяжести сечения.
Положение нейтральной линии определяется отрезками, отсекаемыми ею на главных осях сечения.
или
; 
,
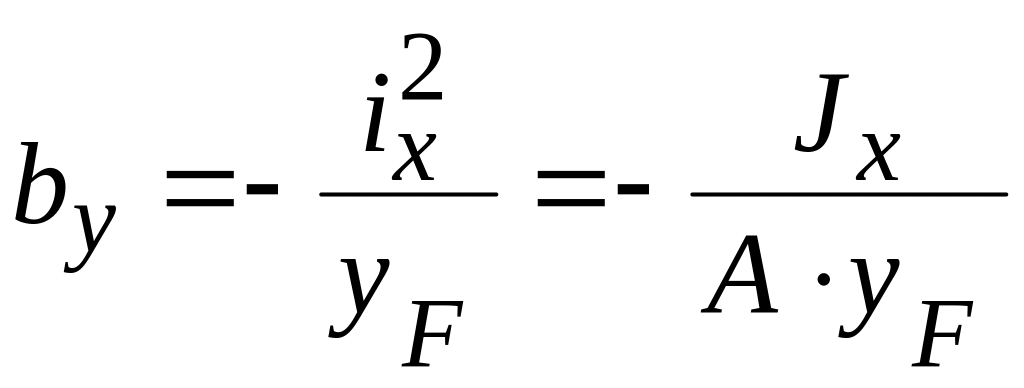где
,
- координаты
точки приложения внецентренной
приложенной силы
;
,
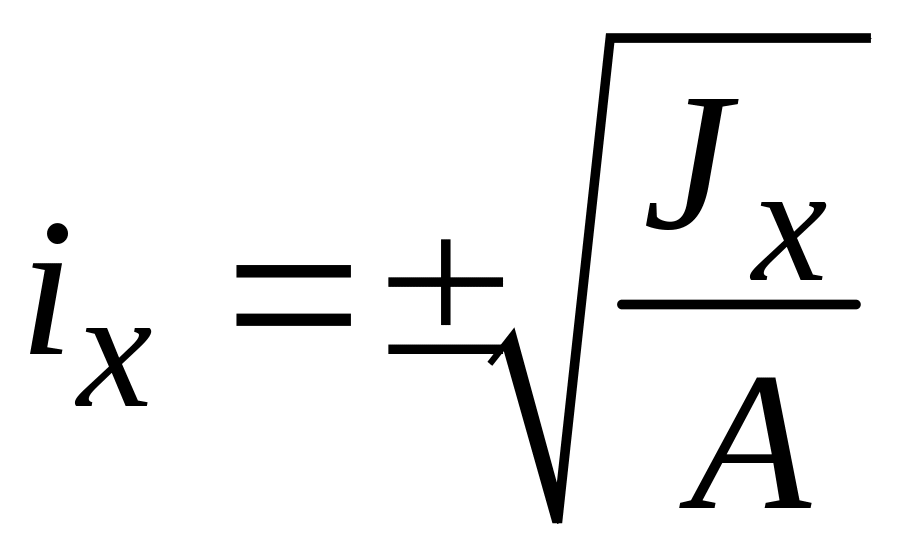- радиусы инерции сечения. Знак минус
показывает, что отрезки
и
откладываются противоположно координатам
,
точки приложения силы
.
Область
около центра тяжести сечения, при
приложении внутри которой сжимающей
силы
,
все сечение испытывает действие только
сжимающих результирующих нормальных
напряжений, называется ядром сечения.
Построение ядра сечения проводится по
координатам точек приложения сжимающей
силы
при обкатывании нейтральной линии по
внешнему контуру сечения в соответствии
с рисунком 5.6
Рисунок 5.6
Для круглого сечения
при
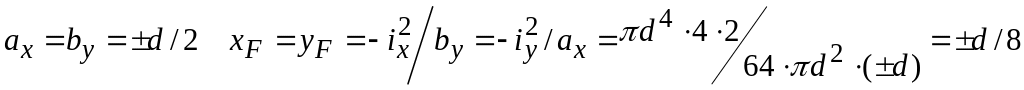
Для прямоугольного сечения
при
,
при
,
,
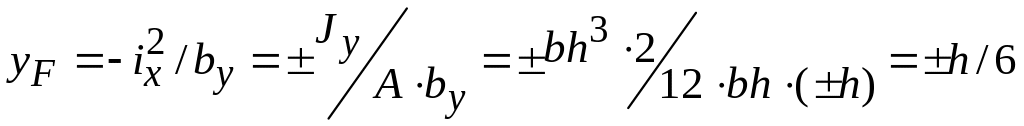Пример 18. Для колонны из четырёх уголков
№
и четырех пластин размерами 20х1,0 см,
нагруженной внецентренно приложенной
продольной силой F,
определить её допускаемую величину при
коэффициенте запаса прочности
.
Длина стойки
,
координаты точки приложения силы
,
в соответствии с рисунком 5.7 а
Ход решения
1. Строим эпюры внутренних силовых
факторов, рассматривая отсеченную
часть колонны со свободного конца, в
соответствии с рисунком 5.7б.
,
,
.
Таким образом, все внутренние силовые
факторы по высоте колонны постоянны.
Все сечения колонны находятся в состоянии
внецентренного сжатия.
2. Определяем опасное сечение. Так как размеры поперечного сечения по высоте стойки постоянны, то все сечения равноопасны.
3. Определяем опасные точки сечений. Для
этого строим эпюры нормальных напряжений
от
,
в соответствии с рисунком 5.7в. По
полученным эпюрам видно положение
опасных точек: точка 1 в сжатой и точка
2 в растянутой частях сечения.
4. Составляем условие прочности для точки 1 с максимальным результирующим сжимающим напряжением. Знаки напряжений в точке сечения от определяем по эпюрам напряжений.
или
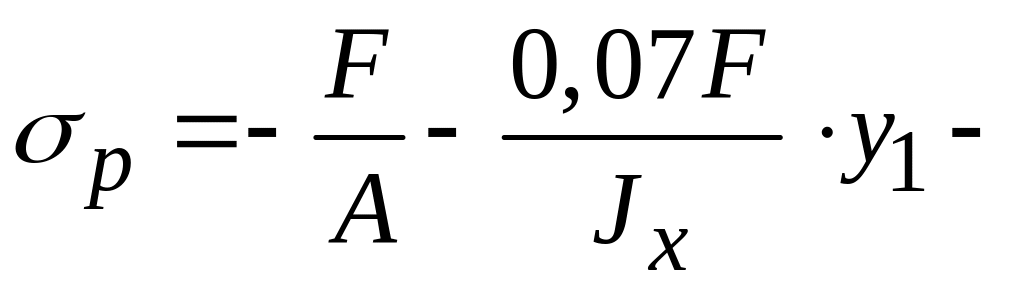
Отсюда
,
где
см,
см координаты точки 1;
-
допускаемое нормальное напряжение;
Рисунок 5.7
,
-
геометрические
характеристики составного сечения
(см. пример 2).
5. Строим эпюру результирующих напряжений, в соответствии с рисунком 5.7в.
Для этого определяем положение нейтральной линии по отрезкам, отсекаемым ею на осях х, у.
Отрезок
.
Отрезок
.
Знак минус в ответах указывает, что
отрезки
и
откладываются противоположно координатам
и
.
По найденной нагрузке определяем напряжения для точки 1
От
От
От
Тогда результирующие напряжения:
- в
точке 1 
- в
точке 2 
По найденным напряжениям строим эпюру результирующих нормальных напряжений.
6. Строим ядро сечения, обкатывая нейтральную линию по внешнему контуру сечения.
При
=
2,99
см
При
По найденным отрезкам строим ядро
сечения в соответствии с рисунком 5.7 в.