5 Сложное сопротивление
5.1 Основные понятия и формулы
Состояние стержня, при котором в его сечениях действует одновременно все или несколько внутренних силовых факторов, называется сложным сопротивлением. Внутренние силовые факторы вызывают в сечениях действие нормальных и касательных напряжений. Рисунок 5.1а. Однако при сложном сопротивлении гипотеза плоских сечений не соблюдается. Результирующая величина нормальных, касательных напряжений и перемещений, определяется на основании принципа независимости действия сил.
Результирующее
нормальное напряжение равно алгебраической
сумме нормальных напряжений от продольной
силы
и изгибающих моментов
и распределяется по площади сечения
по закону прямой от нуля в нейтральном
слое до максимального значения в наиболее
удаленных точках поверхностных слоев.
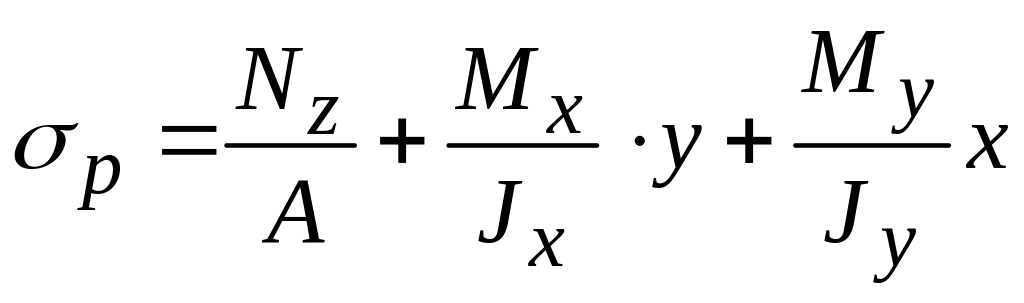
Рисунок 5.1
Линия
сечения, в которой нормальные
результирующие напряжения равны нулю,
называется нейтральной линией. Положение
нейтральной линии определяется по
формуле нейтральной линии
.
где
- координаты точек нейтральной линии.
Результирующее
касательное напряжение равно геометрической
сумме касательных напряжений от
поперечных сил
,
и крутящего момента
.
Материал большинства точек сечения испытывает плоское напряженное состояние в соответствии с рисунокм 5.1 б и условие прочности записывается по одной из теорий прочности.
По
III
теории прочности
По
IV
теории прочности
В зависимости от сочетания действующих в сечении внутренних силовых факторов существуют 5 видов сложного сопротивления.
1. Состояние стержня, при котором в его сечениях действуют все 6 внутренних силовых факторов, называется общим случаем сложного сопротивления.
2.
Состояние стержня, при котором в его
сечениях действуют поперечные силы
,
,
изгибающие моменты
,
и продольная сила
,
а крутящий момент
,
называется косым изгибом с
растяжением-сжатием.
3.
- поперечный изгиб.
4.
- внецентренное растяжение-сжатие.
5.
- совместный изгиб с кручением.
5.2 Косой изгиб. Основные понятия и формулы.
Состояние стержня, при котором в его сечениях действуют поперечные силы , и изгибающие моменты , , называется косым изгибом.
Результирующее нормальное напряжение равно алгебраической сумме нормальных напряжений от изгибающих моментов , и распределяется по сечению по закону прямой от нуля в нейтральном слое до максимального значения в наиболее удаленных точках поверхностных слоев, в соответствии с рисунком 5.2 а
Рисунок 5.2
Касательное результирующее напряжение равно геометрической сумме касательных напряжений от поперечных сил , и распределяются по сечению по закону квадратной параболы от нуля в наиболее удаленных от нейтрального слоя точках поверхностных слоев до максимального значения в точках нейтрального слоя.
В
любой точке сечения
Уравнение
нейтральной линии
- уравнение прямой проходящей через
начало координат сечения. Положение
нейтральной линии определяется углом
ее наклона к оси у
сечения.
,
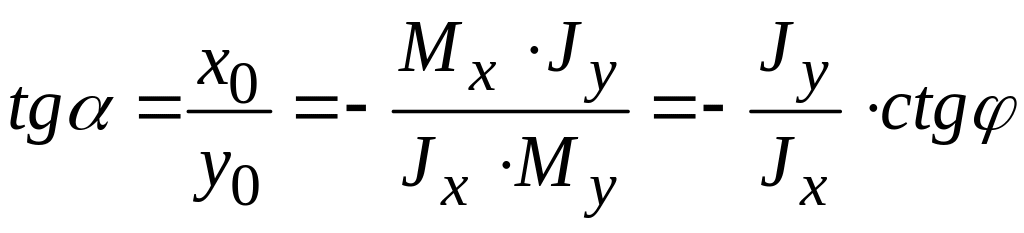где
угол
- угол наклона силовой линии к вертикальной
оси
сечения.
Знак минус показывает, что угол
откладывается от оси
противоположно углу
силовой линии.
Так
как касательные напряжения в наиболее
удаленных опасных точках сечения равны
нулю, то условие прочности при косом
изгибе записывается по максимальному
результирующему нормальному напряжению
.
По
условию прочности решаются задачи для
сечений, имеющих хотя бы одну ось
симметрии при
.
При
косом изгибе плоскость изгиба не
совпадает с главными плоскостями
сечения. Результирующий прогиб любого
сечения равен геометрической сумме
прогибов в горизонтальной и вертикальной
плоскостях сечения
в соответствии с рисунком 5.2 б.
По модулю
Направление
результирующего прогиба определяется
углом
.
Условие жесткости записывается формулой
.