
- •Обозначения и основные символы
- •Содержание
- •Предисловие
- •1.1 Основные положения
- •1.2 Вопросы и ответы для самоконтроля
- •2. Геометрические характеристики плоских сечений
- •2.1 Основные понятия и формулы
- •2.2 Расчетно-проектировочная работа № 1 «Геометрические характеристики плоских сечений»
- •2.3 Вопросы и ответы для самоконтроля
- •3 Внутренние силовые факторы
- •3.1 Основные понятия и формулы
- •3.2 Расчётно-проектировочная работа № 2 «Построение эпюр внутренних силовых факторов»
- •Ход решения
- •Ход решения
- •3.4. Вопросы и ответы для самоконтроля
- •4. Простые состояния стержней
- •4. 1 Состояние растяжения - сжатия. Основные понятия
- •Расчётно-проектировочная работа № 3. «Расчёты на прочность и жёсткость при простых состояниях стержней»
- •4.3 Вопросы и ответы для самоконтроля
- •4.4 Состояние кручения валов круглого сечения. Основные понятия и формулы.
- •4.5 Вопросы и ответы для самоконтроля
- •4.6 Состояние чистого изгиба. Основные понятия и формулы
- •4.7 Состояние поперечного изгиба. Основные понятия и формулы.
- •2. Строим эпюры внутренних силовых факторов
- •5. Производим подбор сечения
- •2. Строим эпюры поперечной силы и изгибающего момента
- •4.8 Вопросы и ответы для самоконтроля
- •5 Сложное сопротивление
- •5.1 Основные понятия и формулы
- •5.2 Косой изгиб. Основные понятия и формулы.
- •Расчетно-проектировочная работа № 4 « Расчеты на прочность при сложном сопротивлении»
- •5.4 Вопросы и ответы для самоконтроля
- •Внецентренное растяжение-сжатие. Основные понятия и формулы.
- •5.6 Вопросы и ответы для самоконтроля
- •5.7 Совместный изгиб с кручением. Основные понятия и формулы.
- •5.8 Вопросы и ответы для самоконтроля
- •6 Определение перемещений энергетическими методами.
- •6.1 Основные понятия и формулы
- •6.2 Расчётно-проектировочная работа № 5 «Определение перемещений при изгибе и решение статически неопределимой задачи»
- •6.3 Вопросы и ответы для самоконтроля
- •7 Устойчивость продольно сжатых стержней
- •7.1 Основные понятия и формулы
- •7.2 Расчётно-проектировочная работа № 6 «Расчёты на устойчивость продольно сжатых стержней»
- •7. 3 Вопросы и ответы для самоконтроля
- •8. Переменные напряжения
- •8.1 Основные понятия и формулы.
- •8.2 Расчётно-проектировочная работа № 7 «Проверочный расчёт вала по условиям усталостной прочности»
- •8.3 Вопросы и ответы для самоконтроля
- •Литература
- •Приложения
- •Сортамент прокатной стали
Расчётно-проектировочная работа № 3. «Расчёты на прочность и жёсткость при простых состояниях стержней»
Пример
10. Для заданного стержня построить эпюру
продольной силы, определить размеры
сечений по участкам и построить эпюру
перемещений сечений. Материал стержня
конструкционная сталь марки Ст.3,
допускаемое напряжение
![]() ,
модуль нормальной упругости
,
модуль нормальной упругости
![]() ,
,
![]() .
Длина участков а = 1 м, b
= 3 м, с = 2 м, в соответствии с рисунком
4.3 а.
.
Длина участков а = 1 м, b
= 3 м, с = 2 м, в соответствии с рисунком
4.3 а.
Ход решения.
Определяем реакцию опоры.
![]() Отсюда
Отсюда
![]()
2. Строим эпюру продольной силы. Построение её рекомендуется начинать от жёстко защемленной опоры.
Для
участка АВ
![]() .
.
Для участка ВС
![]() - уравнение прямой
- уравнение прямой 
Для участка СD
![]() .
.
По найденным значениям строим эпюру продольной силы по всем участкам в соответствии с рисунком 4.3 б.
3. Определяем опасные сечения по участкам.
Для
участка АВ все сечения равноопасны с
![]() кН. Для участка ВС опасное сечение В с
кН. Для участка ВС опасное сечение В с
![]() .
Для участка DC все сечения
равноопасны с
.
Для участка DC все сечения
равноопасны с
![]() = 20 кН.
= 20 кН.
4. Определяем опасные точки опасных сечений. При растяжении-сжатии в поперечных сечениях действуют нормальные напряжения, которые по сечениям распределяются равномерно, в соответствии с рисунком 4.3д .
При растяжении напряжения считаются положительными и направлены от сечения, при сжатии – отрицательными, и направлены к сечению. Из построенных эпюр видно, что при растяжении-сжатии все точки опасных сечений равноопасны.
5.
Определяем размеры сечений по участкам
из условия прочности при растяжении-сжатии.
![]()
Для участка АВ определяем размеры квадратного сечения
![]() Отсюда
Отсюда
![]() см2
см2
![]()
![]() .
.
Для участка ВС определяем размеры круглого сечения
![]() .
Отсюда
.
Отсюда
![]() см2
см2


Рисунок 4.3
![]()
![]() .
.
Для участка СD определяем размеры кольцевого сечения
![]() .
Отсюда
.
Отсюда
![]() 1,25
см2
1,25
см2
![]() ;
;
 .
.
![]() .
.
Проводим проверку прочности для определённых размеров сечений. Для участка АВ

Для участка ВС
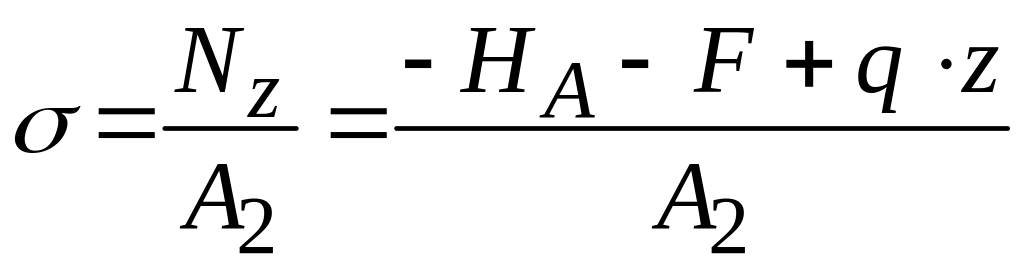 - уравнение прямой
- уравнение прямой ![]()
Для участка DC
![]()
Так как напряжения в опасных сечениях равны допускаемым, то размеры сечений определены верно. По найденным напряжениям строим их эпюры по длине стержня и для опасных сечений в соответствии рисунками 4.3 в,д.
6. По условию жесткости при растяжении – сжатии определяем перемещения сечений и строим эпюру перемещений в соответствии с рисунком 4.3 г.
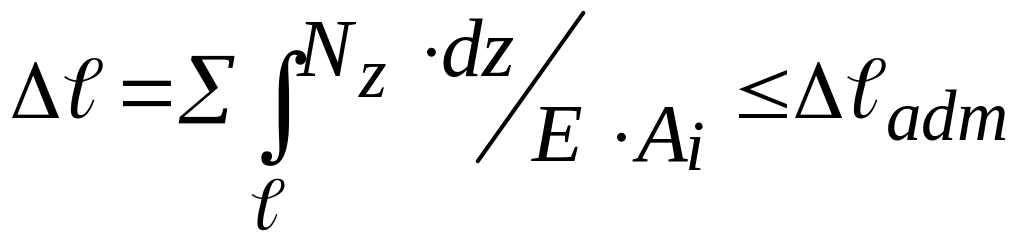
Для участка АВ
 - уравнение прямой.
- уравнение прямой.
![]()
![]() .
.
Для участка ВС
 - уравнение квадратной параболы.
- уравнение квадратной параболы.
![]()
![]() Исследуем
уравнение перемещений на участке ВС на
экстремальное значение
Исследуем
уравнение перемещений на участке ВС на
экстремальное значение
![]() Отсюда
Отсюда
![]()
![]()
Исследуем уравнение перемещений на выпуклость
![]() .
Следовательно, выпуклость эпюры
.
Следовательно, выпуклость эпюры
![]() вниз
вниз
Для участка CD
 - уравнение прямой
- уравнение прямой
![]()
![]()
Определяем суммарные значения эпюры перемещений.
Для сечения
А
![]() .
Для сечения В
.
Для сечения В
![]()
Для сечения
z*= 2м
![]()
Для сечения С
![]()
Для сечения D
![]()
Примечание.
Если координата z*
выходит за пределы размера участка, то
на этом участке экстремальное значение
![]() отсутствует.
отсутствует.
Пример 11. Для стержня, один конец которого
жестко защемлен, а второй имеет зазор
![]() 0,10
мм, определить размеры поперечных
сечений по участкам и построить эпюру
перемещений сечений. Материал стержня
сталь марки Ст.3, предел текучести
0,10
мм, определить размеры поперечных
сечений по участкам и построить эпюру
перемещений сечений. Материал стержня
сталь марки Ст.3, предел текучести
![]() МПа, модуль нормальной упругости
МПа, модуль нормальной упругости
![]() МПа, коэффициент запаса прочности
МПа, коэффициент запаса прочности
![]() .
Длина участков
.
Длина участков
![]() м,
м,
![]() м,
м,
![]() м в соответствии с рисунком 4.4а.
м в соответствии с рисунком 4.4а.
![]() кН,
кН,
![]() кН,
кН,
![]() =10
см2,
=10
см2,
![]()
При приложении внешних нагрузок стержень
будет деформироваться до закрытия
зазора
![]() и в опорах возникнут реакции
и в опорах возникнут реакции
![]() и
и
![]() .
.

Рисунок 4.4
Ход решения
1. Составляем уравнение равновесия стержня
![]()
![]() -
число уравнений равновесия статики
-
число уравнений равновесия статики
2. Определяем степень статической неопределимости системы
![]() - система один раз статически неопределима.
- система один раз статически неопределима.
где
![]() - число неизвестных реакций опор.
- число неизвестных реакций опор.
3. Составляем уравнение совместности
деформаций
![]()
![]() -
перемещение сечения D
стержня от действия системы внешних
нагрузок F1 и
F2.
-
перемещение сечения D
стержня от действия системы внешних
нагрузок F1 и
F2.
 - перемещение сечения D стержня от
действия реакции
.
Тогда
- перемещение сечения D стержня от
действия реакции
.
Тогда
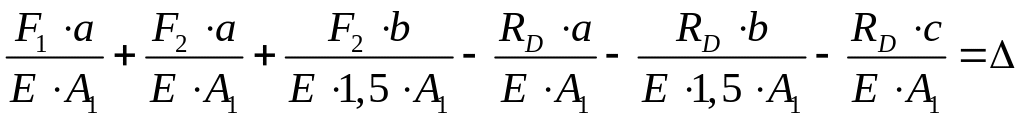 Отсюда
Отсюда
![]()
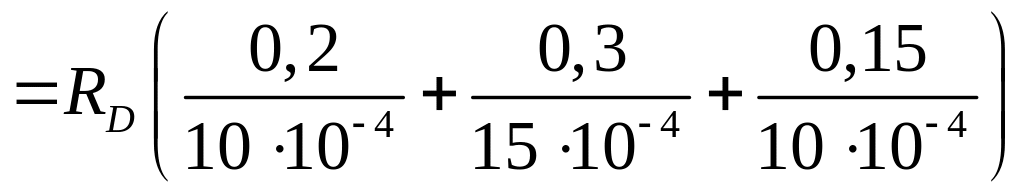
![]() кН.
кН.
Тогда
![]() кН
кН
4. Строим эпюру продольной силы Nz по всем участкам
Для участка АВ
![]() кН-
кН-
Для участка ВС
![]() кН-
кН-
Для участка CD
![]() кН-
кН-
По найденным значениям строим эпюру продольной силы по всем участкам в соответствии с рисунком 4.4б.
5. Проводим проверку прочности по условию
прочности при растяжении-сжатии
![]()
где
![]() МПа – допускаемое напряжение на
растяжение-сжатие для Ст.3
МПа – допускаемое напряжение на
растяжение-сжатие для Ст.3
Для
участка АВ
 МПа
МПа
Для
участка ВС
 МПа
МПа
Для
участка СD
 МПа
МПа
Действующие напряжения в сечениях всех
участков меньше допускаемого напряжения
![]() .
По найденным значениям строим эпюру
напряжений по всем участкам стержня в
соответствии с рисунком 4.4 в.
.
По найденным значениям строим эпюру
напряжений по всем участкам стержня в
соответствии с рисунком 4.4 в.
6. Строим эпюру перемещений Так как продольная сила на всех участках постоянна, то перемещения на каждом из участков изменяются по закону прямой и определяются по формуле
![]()
Для
участка АВ
При
![]()
При
 мм
мм
Для
участка ВС
При
![]()
При

Для
участка СD
При
![]()
При
![]()
 мм
мм
По найденным значениям строим эпюру суммарных перемещений по всем участкам в соответствии с рисунком 4.4 г.
![]()
![]() мм
мм
![]() мм
мм
![]() мм
мм
Пример № 12 Для стержня, оба конца которого
жестко защемлены, определить размеры
поперечных сечений по участкам, построить
эпюры продольной силы, напряжений и
перемещений сечений. Материал стержня
сталь марки Ст.3, предел текучести
МПа, коэффициент запаса прочности
.
Нагрузки
![]() кН,
кН,
![]() кН, длина участков
кН, длина участков
![]() м, b= 0,3 м,
м, b= 0,3 м,
![]() м в соответствии с рисунком 4.5а.
Площадь сечений участков с меньшей
площадью А, с большей площадью 1,5А.
м в соответствии с рисунком 4.5а.
Площадь сечений участков с меньшей
площадью А, с большей площадью 1,5А.

Рисунок 4.5
Ход решения
1. Составляем уравнение равновесия
статики
![]()
2. Определяем степень статической неопределимости системы. Для этого составляем основную и эквивалентные системы. Рисунки 4.5 б, в.
![]() -
система один раз статически неопределима.
-
система один раз статически неопределима.
где
![]() - число неизвестных реакций опор;
- число неизвестных реакций опор;
![]() - число уравнений равновесия статики.
- число уравнений равновесия статики.
3. Составляем уравнение совместности
деформаций
![]()
![]() - перемещение сечения D
под действием системы внешних сил F1,
F2
- перемещение сечения D
под действием системы внешних сил F1,
F2
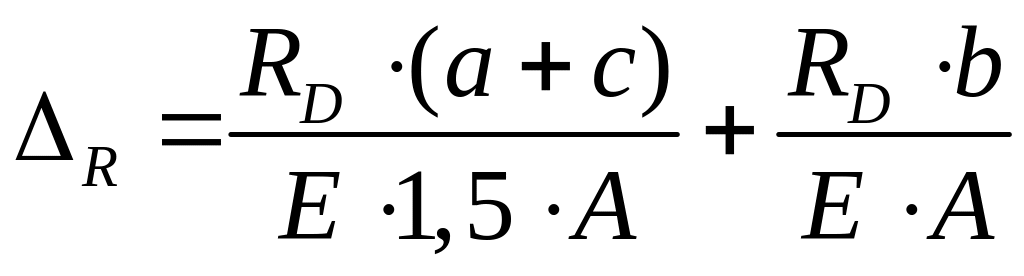 -
перемещение сечения D под действием
реакции
.
Тогда
-
перемещение сечения D под действием
реакции
.
Тогда
 Отсюда
Отсюда

![]() кН
кН
Из
уравнения равновесия
![]() кН
кН
4. Строим эпюру продольной силы по участкам
Для
участка АВ
![]() кН-
кН-
Для
участка ВС
![]() кН-
кН-
Для
участка СD
![]() кН-
кН-
По найденным значениям строим эпюру продольной силы по всем участкам стержня в соответствии с рисунком 4.5г.
5. Из условия прочности при растяжении-сжатии
 определяем размеры сечений по участкам.
определяем размеры сечений по участкам.
Для
участка СD
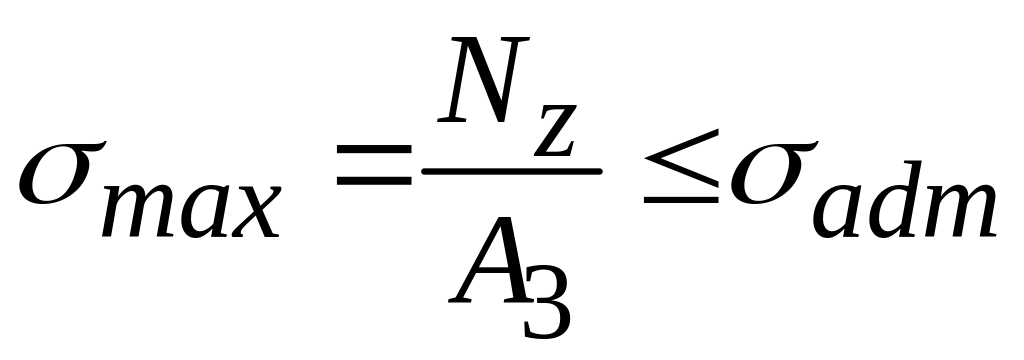 .
Отсюда
.
Отсюда

![]() см2 Тогда
см2 Тогда
![]() см2.
см2.
Для
участка АВ
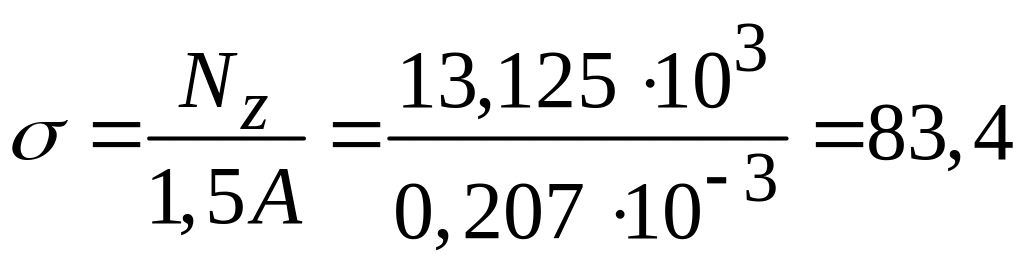 МПа -
МПа -
Для
участка ВС
 МПа -
МПа -
Для
участка СD
 МПа -
МПа -
Так
как
![]() ,
то размеры сечений определены верно.
,
то размеры сечений определены верно.
Так как продольная сила на каждом участке величина постоянная, то и напряжения на каждом участке величины постоянные. Для найденных размеров сечений строим эпюру напряжений по длине стержня. Рисунок 4.5д.
6. Строим эпюру перемещений по длине стержня. Так как продольная сила на всех участках постоянна, то перемещения на каждом из участков изменяются по закону прямой.
Для
участка АВ. При
![]()
При
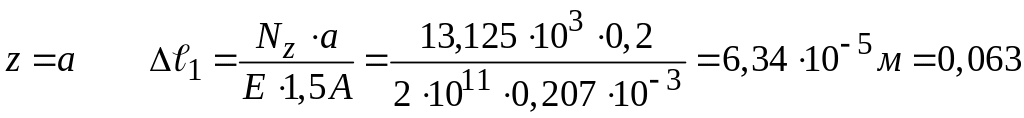 мм
мм
Для
участка ВС. При
![]()
При
 мм
мм
Для
участка CD При
![]()
При
 мм
мм
По найденным значениям строим эпюру
суммарных перемещений по всем участкам
в соответствии с рисунком 4.5е. Для
сечения А
![]() ,
мм. Для сечения В
,
мм. Для сечения В
![]() мм
Для сечения С
мм
Для сечения С
![]() мм.
Для сечения D
мм.
Для сечения D
![]()
