9. Круговые процессы

Круговым процессом (или циклом) называется процесс, при котором система, проходя через ряд состояний, возвращается в первоначальное. На диаграмме цикл изображается замкнутой кривой (рис. 1). Цикл, который совершает идеальный газ, можно разбить на процессы расширения (1—2) и сжатия (2—1) газа. Работа расширения (равна площади фигуры 1a2V2V11) положительна (dV>0), работа сжатия (равна площади фигуры 2b1V1V22) отрицательна (dV<0). Следовательно, работа, которую совершает газ за цикл, равен площади, охватываемой замкнутой кривой. Если за цикл совершается положительная работа A=∫pdV>0 (цикл идет по часовой стрелке), то он называется прямым (рис. 1, а), если за цикл осуществляется отрицательная работа A=∫pdV<0 (цикл идет против часовой стрелки), то он называется обратным (рис. 1, б).

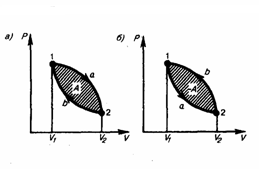
Прямой цикл применяется в тепловых двигателях — периодически действующих двигателях, которые совершают работу за счет полученной извне теплоты. Обратный цикл применяется в холодильных машинах — периодически действующих установках, в которых за счет работы внешних сил теплота переходит к телу с более высокой температурой.

В результате кругового процесса система возвращается в исходное состояние и, значит, полное изменение внутренней энергии газа есть нуль. Поэтому первое начало термодинамики для кругового процесса

(1)

т. е. работа, которая совершается за цикл, равна количеству теплоты, полученной извне. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому

Q = Q1 - Q2

где Q1 — количество теплоты, которая получила система, Q2 — количество теплоты, которое отдала система. Поэтому термический коэффициент полезного действия для кругового процесса

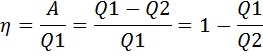
термодинамический процесс называется обратимым, если он может осуществляться как в прямом, так и в обратном направлении, причем если такой процесс осуществляется сначала в прямом, а затем в обратном направлении и система возвращается в первоначальное состояние, то в окружающей среда и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.

Любой равновесный процесс является обратимым. Обратимость равновесного процесса, который происходит в системе, следует из того, что любое промежуточное состояние является состоянием термодинамического равновесия; для него не имеет значения, идет процесс в прямом или обратном направлении. Реальные процессы также сопровождаются диссипацией энергии (из-за трения, теплопроводности и т. д.), которая здесь нами не обсуждается. Обратимые процессы — это идеализация реальных процессов. Их исследование важно по двум причинам: 1) многие процессы в природе и технике практически обратимы; 2) обратимые процессы являются наиболее экономичными; имеют максимальный термический коэффициент полезного действия (КПД), что позволяет указать пути повышения КПД реальных тепловых двигателей.

10.Энтропия…

Понятие энтропии впервые введено в 1865 г. Р. Клаузиусом. Для определения физического содержания этого понятия берут отношение теплоты Q, которое получило тело в изотермическом процессе, к температуре Т теплоотдающего тела, называемое приведенным количеством теплоты.

Приведенное количество теплоты, которое сообщается телу на малом участке процесса, равно δQ/T. Строгий формальный анализ показывает, что приведенное количество теплоты, которое сообщается телу в любом обратимом круговом процессе, равно нулю:

(1)

Из равенства нулю интеграла (1), взятого по замкнутому контуру, следует, что подынтегральное выражение δQ/T есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, которым система пришла в это состояние. Таким образом,

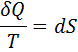
(2)

Функция состояния, у которой дифференциал равен δQ/T, называется энтропией и обозначается S.

Из формулы (1) следует, что для обратимых процессов изменение энтропии

∆S = 0

(3)

В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает:

∆S>0

(4)

Выражения (3) и (4) применяются только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя произвольным образом. Соотношения (3) и (4) можно представить в виде неравенства Клаузиуса

∆S≥0

(5)

т. е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

Если система совершает равновесный переход из состояния 1 в состояние 2, то, согласно (2), изменение энтропии

∆S_1→2=S2-S1= (6)

где подынтегральное выражение и пределы интегрирования определяются через величины, которые характеризуют рассматриваемый процесс. Формула (6) определяет энтропию лишь с точностью до аддитивной постоянной (слагаемого). Физический смысл имеет не сама энтропия, а разность энтропий.

Используя выражение (6), найдем изменение энтропии в процессах идеального газа. Taк как dU=(m/M)CVdT, δA=pdV=(m/M)RT(dV/V) , то

∆S_1→2=S2-S1=

или

∆S_1→2=S2-S1=

(7)

т. е. изменение энтропии ΔS1→2 идеального газа при переходе его из cоcтояния 1 в cоcтояние 2 не завиcит от вида процеccа перехода 1→2.

Так как для адиабатического процесса δQ = 0, то ΔS = 0 и, следовательно, S=const, т. е. адиабатический обратимый процесс протекает при постоянной энтропии. Поэтому его часто называют изоэнтропийным процессом. Из формулы (7) следует, что при изотермическом процессе (T1= T2)

∆S=(m/M)*R*ln(V2/V1)

при изохорном процессе (V1 = V2)

∆S=(m/M)*C_V*ln(T2/T1)

Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропий тел, которые входят в систему. Свойством аддитивности обладают также внутренняя энергия, масса, объем (но таким свойством не обладают температура и давление).

Более глубокий смысл энтропии показывается в статистической физике: энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность W состояния системы — это число способов, с помощью которых может быть реализовано данное состояние макроскопической системы, или число микросостояний, которые осуществляют данное макросостояние (по определению, W≥1, т. е. термодинамическая вероятность не есть вероятность в математическом смысле (последняя ≥1 !!!)).

Cогласно Больцману, энтропия cиcтемы и термодинамическая вероятность связаны между собой следующим образом:

S=k*lnW

(8)

где k — постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть осуществлено данное макросостояние. Значит, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана (8) позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. Действительно, чем больше число микросостояний, которые реализуют данное макросостояние, тем больше энтропия. В состоянии равновесия — наиболее вероятного состояния системы — число микросостояний максимально, при этом также максимальна и энтропия.

Так как реальные процессы необратимы, то можно говорить, что все процессы в замкнутой системе ведут к увеличению ее энтропии — принцип возрастания энтропии. При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, другими словами, от менее вероятных состояний к более вероятным, до тех пор пока вероятность состояния не станет максимальной.

Соотнося выражения (5) и (8), видим, что энтропия и термодинамическая вероятность состояний замкнутой системы могут либо увеличиваться (в случае необратимых процессов), либо оставаться неизменными (в случае обратимых процессов).

Отметим, однако, что эти утверждения имеют место для систем, которые состоят из очень большого числа частиц, но могут нарушаться в системах с малым числом частиц. Для систем с малым числом частиц могут наблюдаться флуктуации, т. е. энтропия и термодинамическая вероятность состояний замкнутой системы на фиксированном отрезке времени могут уменьшаться, а не увеличиваться, или оставаться постоянными.