Лабораторная работа № 3 Хэширование
Цель работы: ознакомиться с операцией хэширования, выполненного различными способами.
Общие теоретические положения:
Хеширование (иногда хэширование, англ. hashing) — преобразование входного массива данных произвольной длины в выходную битовую строку фиксированной длины. Такие преобразования также называются хеш-функциями или функциями свёртки, а их результаты называют хешем, хеш-кодом или дайджестом сообщения (англ. message digest).
Хеширование применяется для сравнения данных: если у двух массивов хеш-коды разные, массивы гарантированно различаются; если одинаковые — массивы, скорее всего, одинаковы. В общем случае однозначного соответствия между исходными данными и хеш-кодом нет в силу того, что количество значений хеш-функций меньше, чем вариантов входного массива; существует множество массивов, дающих одинаковые хеш-коды — так называемые коллизии. Вероятность возникновения коллизий играет немаловажную роль в оценке качества хеш-функций.
Существует множество алгоритмов хеширования с различными характеристиками (разрядность, вычислительная сложность, криптостойкость и т. п.). Выбор той или иной хеш-функции определяется спецификой решаемой задачи. Простейшими примерами хеш-функций могут служить контрольная сумма или CRC.
Контрольные суммы
Несложные, крайне быстрые и легко реализуемые аппаратные алгоритмы, используемые для защиты от непреднамеренных искажений, в том числе ошибок аппаратуры.
По скорости вычисления в десятки и сотни раз быстрее, чем криптографические хеш-функции, и значительно проще в аппаратной реализации.
Платой за столь высокую скорость является отсутствие криптостойкости — лёгкая возможность подогнать сообщение под заранее известную сумму. Также обычно разрядность контрольных сумм (типичное число: 32 бита) ниже, чем криптографических хешей (типичные числа: 128, 160 и 256 бит), что означает возможность возникновения непреднамеренных коллизий.
Простейшим случаем такого алгоритма является деление сообщения на 32- или 16- битные слова и их суммирование, что применяется, например, в TCP/IP.
Как правило, к такому алгоритму предъявляются требования отслеживания типичных аппаратных ошибок, таких, как несколько подряд идущих ошибочных бит до заданной длины. Семейство алгоритмов т. н. «циклических избыточных кодов» удовлетворяет этим требованиям. К ним относится, например, CRC32, применяемый в аппаратуре Ethernet и в формате упакованных файлов ZIP.
Криптографические хеш-функции
Среди множества существующих хеш-функций принято выделять криптографически стойкие, применяемые в криптографии. Для того чтобы хеш-функция H считалась криптографически стойкой, она должна удовлетворять трем основным требованиям, на которых основано большинство применений хеш-функций в криптографии:
Необратимость: для заданного значения хеш-функции m должно быть вычислительно неосуществимо найти блок данных
,
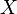для которого
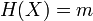.Стойкость к коллизиям первого рода: для заданного сообщения M должно быть вычислительно неосуществимо подобрать другое сообщение N, для которого
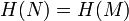.Стойкость к коллизиям второго рода: должно быть вычислительно неосуществимо подобрать пару сообщений
,
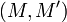имеющих одинаковый хеш.
Задание на работу: Выполнить преобразование номера зачетки в индекс массива двумя способами.
Способ 1
Для преобразования следует выполнить возведение номера зачетки в квадрат, выбрать несколько средних цифр из полученного результата, которое называется вырезкой, и далее вычислить индекс (остаток от деления вырезки на размер диапазона индексов равного 335). Результаты в Таблице 1.
Таблица 1 - Преобразование номера зачетки в индекс массива первым способом
Номер |
Квадрат номера |
Вырезка |
Индекс |
712016 |
506966784256 |
69667842 |
237 |
712017 |
506968208289 |
69682082 |
72 |
712018 |
506969632324 |
69696323 |
243 |
712019 |
506971056361 |
69710563 |
78 |
712020 |
506972480400 |
69724804 |
249 |
712021 |
506973904441 |
69739044 |
84 |
712022 |
506975328484 |
69753284 |
254 |
712023 |
506976752529 |
69767525 |
90 |
712024 |
506978176576 |
69781765 |
260 |
Способ 2
Для преобразования следует вычислить значение полиномиальной функции по схеме Горнера при диапазоне индексов равном 335 и r = 33 (расчеты приведены в таблице 2). Затем определить накопленные суммы для каждого номера и выделить из них индекс (результаты в таблице 3).
Таблица 2 – Вычисление функции h(d) по схеме Горнера
дипазон |
335 |
число r |
33 |
Номер |
h |
Остаток от деления диапазона |
712016 |
h(7) |
7 |
h(71) |
232 |
|
h(712) |
288 |
|
h(7120) |
124 |
|
h(71201) |
73 |
|
h(712016) |
70 |
|
712017 |
h(7) |
7 |
h(71) |
232 |
|
h(712) |
288 |
|
h(7120) |
124 |
|
h(71201) |
73 |
|
h(712017) |
71 |
|
712018 |
h(7) |
7 |
h(71) |
232 |
|
h(712) |
288 |
|
h(7120) |
124 |
|
h(71201) |
73 |
|
h(712018) |
72 |
|
712019 |
h(7) |
7 |
h(71) |
232 |
|
h(712) |
288 |
|
h(7120) |
124 |
|
h(71201) |
73 |
|
h(712019) |
73 |
|
712020 |
h(7) |
7 |
h(71) |
232 |
|
h(712) |
288 |
|
h(7120) |
124 |
|
h(71202) |
74 |
|
h(712020) |
97 |
|
712021 |
h(7) |
7 |
h(71) |
232 |
|
h(712) |
288 |
|
h(7120) |
124 |
|
h(71202) |
74 |
|
h(712021) |
98 |
|
712022 |
h(7) |
7 |
h(71) |
232 |
|
h(712) |
288 |
|
h(7120) |
124 |
|
h(71202) |
74 |
|
h(712022) |
99 |
|
712023 |
h(7) |
7 |
h(71) |
232 |
|
h(712) |
288 |
|
h(7120) |
124 |
|
h(71202) |
74 |
|
h(712023) |
100 |
|
712024 |
h(7) |
7 |
h(71) |
232 |
|
h(712) |
288 |
|
h(7120) |
124 |
|
h(71202) |
74 |
|
h(712024) |
101 |
Таблица 3 – Преобразование номера зачетки в индекс массива вторым способом
номер |
накопленные суммы |
индекс |
|||||
712016 |
7 |
232 |
288 |
124 |
73 |
70 |
70 |
712017 |
7 |
232 |
288 |
124 |
73 |
71 |
71 |
712018 |
7 |
232 |
288 |
124 |
73 |
72 |
72 |
712019 |
7 |
232 |
288 |
124 |
73 |
73 |
73 |
712020 |
7 |
232 |
288 |
124 |
74 |
97 |
97 |
712021 |
7 |
232 |
288 |
124 |
74 |
98 |
98 |
712022 |
7 |
232 |
288 |
124 |
74 |
99 |
99 |
712023 |
7 |
232 |
288 |
124 |
74 |
100 |
100 |
712024 |
7 |
232 |
288 |
124 |
74 |
101 |
101 |
Содержание отчета:
Отчет оформляется на формате А4 должен содержать название лабораторной работы, цель, задание и результаты вычисления.