
- •090900 « Информационная безопасность»
- •Лабораторная работа № 1 Симметричные системы шифрования. Методы замены
- •Математическая модель
- •2. Шифр атбаш
- •3. Шифр Полибия
- •Способ шифрования
- •Шаг 1: Формирование таблицы шифрования
- •Русский алфавит
- •Шаг 2: Принцип шифрования
- •Метод 1
- •Метод 2
- •Метод 3
- •4. Шифр Вижинера
- •5. Аффинный шифр.
- •Примеры шифрования и расшифрования
- •Шифрование
- •Расшифрование
- •Лабораторная работа № 2 Симметричные системы шифрования. Методы перестановки
- •Лабораторная работа № 3 Хэширование
- •Контрольные суммы
- •Криптографические хеш-функции
- •Лабораторная работа № 4 Электронные цифровые подписи
- •Новый отечественный стандарт эцп
- •Лабораторная работа № 5 Криптоанализ цифровых подписей
- •Список используемых источников:
4. Шифр Вижинера
Система Вижинера впервые была опубликована в 1586 г. и является одной из старейших и наиболее известных многоалфавитных систем. Свое название она получила по имени французского дипломата XVI века Блеза Вижинера, который развивал и совершенствовал криптографические системы.
Система Вижинера подобна такой системе шифрования Цезаря, у которой ключ подстановки меняется от буквы к букве. Этот шифр многоалфавитной замены можно описать таблицей шифрования, называемой таблицей (квадратом) Вижинера. На рис.10 и 11 показаны таблицы Вижинера для русского и английского алфавитов соответственно.
Таблица Вижинера используется для зашифрования и расшифрования. Таблица имеет два входа:
• верхнюю строку подчеркнутых символов, используемую для считывания очередной буквы исходного открытого текста;
• крайний левый столбец ключа.
Последовательность ключей обычно получают из числовых значений букв ключевого слова.
При шифровании исходного сообщения его выписывают в строку, а под ним записывают ключевое слово (или фразу). Если ключ оказался короче сообщения, то его циклически повторяют. В процессе шифрования находят в верхней строке таблицы очередную букву исходного текста и в левом столбце очередное значение ключа. Очередная буква шифртекста находится на пересечении столбца, определяемого шифруемой буквой, и строки, определяемой числовым значением ключа.
Пусть ключевая последовательность имеет длину r, тогда ключ r-алфавитной подстановки есть r-строка
![]() (9)
(9)
Система
шифрования Вижинера преобразует открытый
текст
![]() в
шифртекст
в
шифртекст
![]() с
помощью ключа
согласно
правилу
с
помощью ключа
согласно
правилу
![]()
![]() (10)
(10)
где
![]() .
.
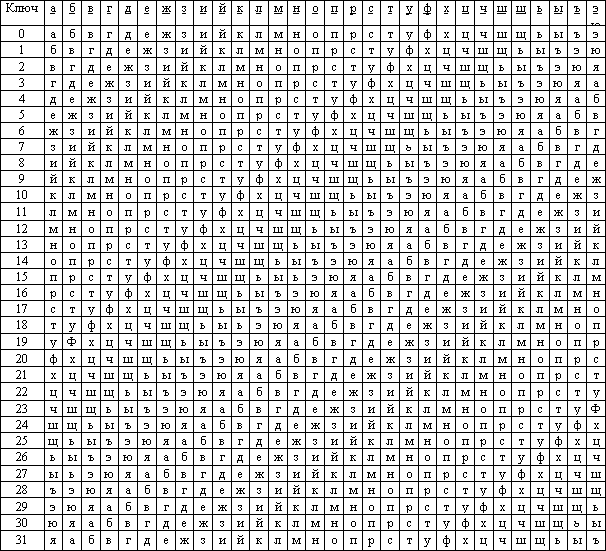 Рис.
1. Таблица Вижинера для русского алфавита
Рис.
1. Таблица Вижинера для русского алфавита
Рассмотрим пример получения шифртекста с помощью таблицы Вижинера. Пусть выбрано ключевое слово АМБРОЗИЯ. Необходимо зашифровать сообщение ПРИЛЕТАЮ СЕДЬМОГО.
Выпишем исходное сообщение в строку и запишем под ним ключевое слово с повторением. В третью строку будем выписывать буквы шифртекста, определяемые из таблицы Вижинера.
Сообщение |
П |
Р |
И |
Л |
Е |
Т |
А |
Ю |
|
С |
Е |
Д |
Ь |
М |
О |
Г |
О |
Ключ |
А |
М |
Б |
Р |
О |
З |
И |
Я |
|
А |
М |
Б |
Р |
О |
З |
И |
Я |
Шифртекст |
П |
Ъ |
Й |
Ы |
У |
Щ |
И |
Э |
|
С |
С |
Е |
К |
Ь |
Х |
Л |
Н |
5. Аффинный шифр.
В
аффинном шифре каждой букве алфавита
размера
![]() ставится
в соответствие число из диапазона
ставится
в соответствие число из диапазона
![]() .
Затем при помощи модульной арифметики
для каждого числа, соответствующего
букве исходного алфавита, вычисляется
новое число, которое заменит старое в
шифротексте. Функция шифрования[
для каждой буквы
.
Затем при помощи модульной арифметики
для каждого числа, соответствующего
букве исходного алфавита, вычисляется
новое число, которое заменит старое в
шифротексте. Функция шифрования[
для каждой буквы
![]()
где модуль
—
размер алфавита, а пара
![]() и
и
![]() —
ключ шифра. Значение
должно
быть выбрано таким, что
и
—
взаимно простые числа. Функция
расшифрования
—
ключ шифра. Значение
должно
быть выбрано таким, что
и
—
взаимно простые числа. Функция
расшифрования
![]()
где
![]() —
обратное к
число
по модулю
.
То есть оно удовлетворяет уравнению
—
обратное к
число
по модулю
.
То есть оно удовлетворяет уравнению
![]()
Обратное к число существует только в том случае, когда и — взаимно простые. Значит, при отсутствии ограничений на выбор числа расшифрование может оказаться невозможным.
