§ 4. Общее уравнение движения подъемного механизма

Работа подъемного механизма буровой установки связана с ча­стыми пусками, остановками, подъемами и спусками ко.чонн раз­личного веса и фактически осуществляется в условиях непрерывно изменяющихся процессов, называемых переходными или нестацио­нарными.

Энергия двигателя, равная работе сил инерции всех неравно­мерно движущихся масс в период неустановившегося движения расходуется в процессе разгона и поглощается механизмом во время торможения.

Продолжительность периода неустановившегося движения является функцией избыточного момента двигателя или тормоза. Основным уравнением переходных процессов является уравнение механического равновесия. При разгоне:

М_№-М„ = М_т. (VI-27)

И* 1G3

При торможении:

л/_дт + л/_ст. = л/_11Я.

Здесь Д/_[у, Af_eT, Л/_ин и А/_дт —соответственно моменты движущего разгона, статических сопротивлений, инерционных сил и тормозной. Например, для перяода разгона барабана лебедки избыточный момент М_пя — это разность между суммой моментов, развива­емых двигателем М_др и вращающихся с ними массами в этот период, и моментов статических сопротивлений Л/_ст, приведенных к бара­бану лебедки; для периода торможения избыточный момент Л/_ИЗбт —

это сумма тормозного момента Л/_дт и момента статических сопроти­влений М_ст1 приведенных к валу барабана лебедки.

Избыточный момент M_u._l(l равен по абсолютной величине моменту инерционных сил масс М_ип, связанных с барабаном лебедки, как это следует из уравнении динамического равновесия, т. е.

При иращательном движения переходные процессы характери­зуются величинами момента инерции / и при поступательном — массой т.

Параметры неустановившегося движения определяются из фор­мулы запаса кинетической энергии системы вращающихся и посту­пательно движущихся масс

__{f =} _ , ₍ vi-28)

где/,., I_r и (o^ — момент инерции, угол поворота и угловая скорость произвольно вращающейся массы относительно ее оси вращения;

m_f, 5, и v_r — масса, путь и линейная скорость поступательно дви­жущейся массы системы.

Например, при разгоне неподвижного барабана лебедки и крюка с грузом при включении фрикционной муфты двигателя с враща­ющимся приводом в момент включения скорость вращения двигателя и вращающихся с ним масс снизится и освобождающая кинетическая энергия k! будет израсходована на разгон барабана лебедки и свя­занных с ним масс.

ЛГ,-/^ /..-, (VJ-29)

где /₍ и /-—приведенные моменты инерции двигателя и лебедки

и связанных с ними масс;

(^ — скорость двигателя в момент включения; ш- — угловая скорость барабана лебедки, равная по вели-

чине приведенной скорости вращения двигателя в кон-

це включения.

104

Отношение отданной кинетической энергии К₁ к исходному ее запасу К_а до начала разгона

Время &

Время t

-М

( VI-30)

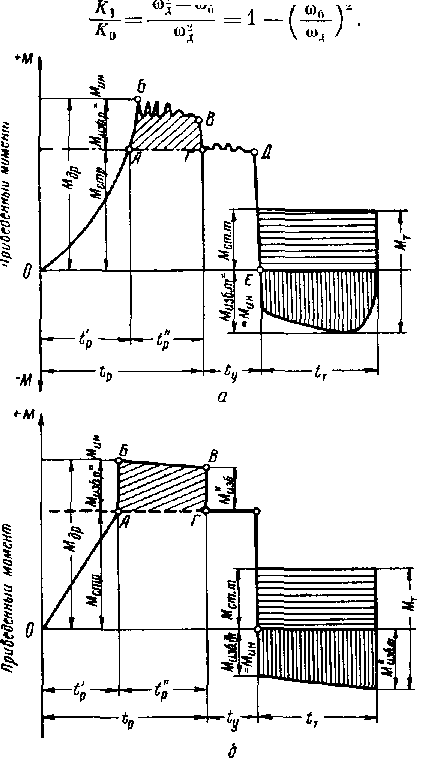
Рис, VI-6. График изменения момента на барабане лебедки при разгоне и тормо­жении.

о—фактический; б—упрощенный. Моменты: М и М —двигателя при разгоне и тормоз­ной; M_Bjfl. р, jUuju. р- М„зг,. _т и Мили- т — избыточные моменты и начале и конце разгона и торможения; М и М —статические моменты при разгоне и торможении; Л/ — инерционный момент; f_p—время разгона талевой системы; (_р—время разгона колонны; t , t_f и t^~общее время разгона, установившегося двигателя и тормошения.

Из этой формулы видно, что отдаваемая кинетическая энергия зависит от квадрата скоростей вращения до и после включения муфтой сцепления вращающейся массы.

Например: если скорость при включении снизится в два раза, т. е. о)₆ = 0,5со_д, то за этот период будет израсходовано на разгон 75% запаса кинетической энергии.

Для приближенных расчетов принимают линейны!!: закон изме­нения ускорения.

На рис. VI-6, б показано изменение момента на барабане лебедки при разгоне и торможении во время произвольного изменения про­цесса и при линейном законе изменения ускорения. На участке ОА (рис. VI-6, а) происходит разгон барабана и связанных с ним частей талевой системы до нагрузки, равной силе тяжести подвешенной на крюке колонны. В точке Л начинается движение крюка с ко­лонной.

На участке АБ расходуется избыточный момент двигателя Л/,, .„-,,.

Если скорость вращения двигателя и связанных с ним масс в точке Б будет меньше, чем в точке Л, то кинетическая энергия, освободив­шаяся за счет замедления вращения, будет затрачиваться на пре­одоление сил сопротивления движению. Если же скорость будет больше (что обычно имеет место), то избыточный момент двигателя -^и.ч'Ф будет расходоваться на преодоление инерции всей движу­щейся системы.

Кинетическую энергию системы можно выразить также через обобщенный параметр, например через момент инерции /₀, приведен­ный к произвольному валу, вращающемуся с угловой скоростью со_п.

Величина этого момента инерции определяется из условия, что отвечающая ему кинетическая энергия равна кинетической энергии данной системы.

2. — ^

Так как инерционный момент Л/_И11 может быть выражен в виде

if — Г ^L - - rVI-Я'^

-"шс — ^J 0 (ftf » V ^{v 1} °~'

то общее уравнение движения механизма можно представить та­ким образом. Для периода разгона

rf2m

^д„ -= ^_СТ. р + M_m = М„ ~ /₀ ^ ; ( VI-33)

для периода торможения

М М —М — Д/ — I ^^2ФТ (VI-34)

^1Идт — ^^нст. т ^jk*hu — ^jk/ct. т ^J0 dfi • \ ^{v 1 J}^>

Здесь Л/_др и Д/_дт — соответственно движущий и тормозной мо­менты, приведенные к тому же валу, что if момент /₀; ф и ф_т — углы поворота рассматриваемого вала в ле-

. риод неустановившегося движения.

В буровых установках, имеющих различные кинематические схемы, разгон крюка осуществляется включением оперативной

166

фрикционной муфты или при пуске двигателя. В первом случае инерционный момент двигателя суммируется с моментом враща­ющихся одновременно с ним масс до муфты включения, а во вто­ром — разгон осуществляется спуском двигателя. Двигатель пре­одолевает инерционный момент всех масс кинематической цепи и инерцию ротора.

Первый случай обычно используется при двигателях внутрен­него сгорания и реже при электродвигателях, второй — только при электродвигателях, так как двигатели внутреннего сгорания иод нагрузкой не запускаются.

Для приближенных расчетов можно использовать линейный закон изменения ускорений, тогда избыточный момент

p-;-f <^.,,--л*;*.р)1 (vi-35)

^{1 (}к J

где t—текущее время;

t_K — время неустановившегося движения; при разгоне £_к =

-^;=£р, а при торможении г_к = £_т;

A/,j_j0 и Л/^_аГ| — избыточные моменты в начальный и конечный пе­риоды неустановившегося движения (рис. VI-6, б); знак плюс относится к периоду разгона, знак минус к периоду торможения.

Уравнения движения для принятых условий из (VI-32) и (VI-35) запишутся: ускорение для периода разгона крюка:

at iq tp jq

для периода торможения

^£t ""^: ~rf/5r" ~~"—Т^~ ~~ 1 ""' ^Т~' "*'' ^Т ' (VI-37)

Угловая скорость барабана для периода разгона крюка:

J^Hlfi П^ Г -^ИЧП 1}— -^ll'iO I. /

HiiU- II I I HdU' p UiiU. u t ,

¹¹ dt =

jq *_P

о „ ⁽ '

Производная постоянная С определяется из начальных усло­вий: при £_р = 0, (о_р=^0; подставляя в полученный интеграл, полу­чим С — 0.

Время разгона ^ при со_р--о)₀

^2/"^(do

Путь разгона

При (~0; <р_р = 0; следовательно, d — 0.

107

Угловая скорость барабана при торможении со_г, время £_т и путь торможения <р_т определяются аналогичным образом из формул (VI-34) и (VI-35).

При разгоне и торможении крюка по закону, соответствующему линейному изменению ускорения, параметры движения барабана лебедки могут быть определены по формулам, приведенным в табл. VJ-2.

Таблица VI-2 Формулы для определения параметров движения

Параметр

Разгон

Торможение

Путь (pp. pad

4V = V

•=-V3fcV_P

Ч Л/ -

'* '"изо

Время /, сек

Скорость to, рад /сек

-^

иэб. р /2

27

0)_T=-- (D|,

-=w₍₍—е_т —

Ускорение е,

рад /сек'*

Аналогично можно определить все параметры движения (путь, время разгона и торможения) для любого закона их изменения.

При недостатке запаса мощности двигателей или несоответствии используемой скорости лебедки величине поднимаемого груза разгон будет иметь затяжной характер и может закончиться за период подъема на всю длину свечи.

В момент начала и окончания разгона или торможения про­исходят толчки, называемые «рывками скорости», выражаемые производной от ускорения или второй производной от скорости

г/с. d2(o <7³ф ,_Л7Т ,.,

Р = ^? ⁼ ^⁼^г- <^Л1-¹*¹)

Если обеспечивается плавное изменение скорости, например

по параболическому закону, «рывка скорости» не будет, что следует

из формулы (VI-41).

В подъемных механизмах с силовыми приводами с двигателями

постоянного тока или дизелями с турботрансформаторами разгон

1G8

происходит примерно но параболическому закону без рывков, в элек­тродвигателях трехфазного переменного тока, особенно синхронных, разгон обычно происходит по линейному закону.

Приведенные уравнения движения используют для анализа подъемных механизмов, определения действующих динамических сил и отыскания путей их снижения.