13. Расчет надежности систем с параллельно-последовательным соединением элементов

Расчет надежности – расчет, в результате которого получаются количественные значения показателей надежности исследуемого объекта. Целью расчета надежности является: сравнение вариантов при выборе технического решения; получение приближенных оценок показателей надежности.

Аналитические методы расчета надежности

Целью расчета является получение оценок, сравнения

для расчета надежности системы используется так называемые структурные схемы: модели надежности систем. Модель надежности строится на основе анализа влияния определенного вида отказов элементов на надежность системы в целом

Рассмотрим несколько таких структурных схем

1)Расчет надежности при последовательном соединении

Последовательным - называется такое соединение, при котором отказ хотя бы одного из них, приводит к отказу всего соединения в целом

Каждый элемент включаемый в структурную схему характеризуется интенсивностью отказов х и вероятностью безотказной работы р. Будем считать, что отказы отдельных элементов независимы между собой → что вероятность безотказной работы какого-либо изделия:

P_c(t)= P₁(t)* P₂(t)… P_n(t)=

Интенсивность отказов изделия λ_c(t)= λ₁(t)+ λ₂(t)+… +λ_n(t)=

структура последовательного соединения

среднее время наработки на отказ Т_с=1/ λ_c

2)Расчет надежности системы с параллельным соединением

Параллельным - называется соединение, при котором отказ всего соединения в целом происходит при отказе всех элементов системы

Вероятность безотказной работы P_c(t)=1-

вероятность отказа Q_c(t)=

3)расчет надежности системы в последовательно-параллельной системе

Вероятность безотказной работы

P₁₂=1-(1-P₁(t))*(1-P₂(t)) P_c(t)= P₁₂(t)* P₃(t)

Постоянная (нагруженное или горячее) резервирование элементов системы

При постоянном резервировании резервные элементы постоянно присоединены к основному и функционируют одновременно с момента включения системы. Такая структура предполагает параллельное соединение

Вероятность отказа системы Q(t)=

Вероятность безотказной работы P(t)=1-Q(t)=1-

Достоинства: простота и экономичность

Недостаток: изменение электрических режимов при отказе какого-либо одного

14. Основные этапы логико-вероятностного подхода

Рассмотрим расчет надежности системы с несводимой к параллельно – последовательным

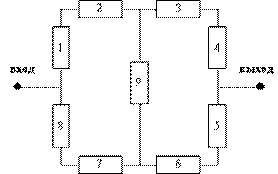
Работоспособность i-того элемента представляется собой функцию:

X_i=

Можно сказать, что функция Х работоспособна и представляет собой

Y=X₁X₂X₃X₄X₅X₆X₇ X₈ X₉˅ X₁X₂X₃X₄X₉˅ X₅X₆X₇ X₈ X₉

Такой метод получил название логико-вероятностный последовательность расчета надежности:

1)сформулировать словесно условие работоспособности изделия

2)согласно этому условию можно (сформировать) записать логическую функцию работоспособности системы на этом же этапе произвести ее

3)минимизацию, исключить цепочки повторений элементов

4)в логической функции произвести замену логическими арифметическими a˅b=a+b-ab

5)замена арифметической функции работоспособности вероятностными

6)в эту формулу подставляются числовые значения этих показателей устанавливают связь между вероятностными состояниями системы и вероятностью состоянию системы в целом

Модель задается в виде состояний, в которых система может находиться n возможных переходов из одного состояния в другое P_c(t)= P_i(t)

Называется метод на основе марковских процессов

Представим систему из трех элементов

λ - показатель интенсивности

μ - показатель ремонтопригодности

Согласно этому графику можно выделить следующие состояния системы:

1)работают оба элемента системы → система работоспособна

2)отказ одного элемента → система работоспособна

3)отказ двух элемент →система неработоспособна

Составим уравнение, в котором производная от вероятности нахождения системы в i-том состоянии равна сумме произведений интенсивности перехода на вероятность соответствующих состояний

Производная от вероятности нахождения системы в i - том состоянии равна алгебраической сумме произведений интенсивности перехода на вероятности соответствующих состояний. Тем произведениям, которым соответствуют уходящие из данного состояния стрелки, приписывают знак "-", а входящим - "+". Таким образом, для данной системы изображенной на рисунке, имеем:

Таким образом, используя приведенные функции можно получить приближенные значения показателей надежности технических объектов, что позволяет проводить анализ при проектировании и производстве систем