22. Модели надежности по

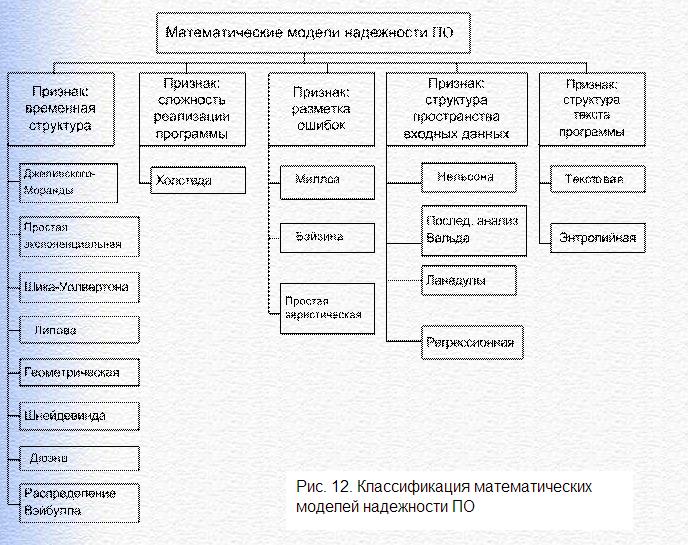
Оценка и прогнозирование надежности программ осуществляется на основе математических моделей надежности программ, которые имеют следующие предпосылки: в начальный момент времени программа работает и сохраняет свою работоспособность до окончания интервала времени t1, когда обнаруживается ошибка в программе. Программист исправляет программу, которая затем исправно работает до t2 и т.д.

Для построения вероятностной модели имеется:

-случайное время между двумя последовательными отказами, к-е имеет функцию плотности распределения f(t/λ) появления ошибок

-число оставшихся ошибок в программе

Самой известной моделью надежности является модель Джелински-Моранды, опирающая на модели надежности аппаратуры.

Пусть R(t) - функция надежности, т.е. вероятность того, что ни одна ошибка не появится в интервале от 0 до t.

F(t)=1-R(t) - функция отказов.

Соответственно плотность вероятности f(t)=-dR(t)/dt.

Вводится функция риска z(t)-условная вероятность тог, что ошибка появится на интервале от t до t+∆t, при условии, что до момента t ошибок не было.

z(t)=f(t)/R(t) , R(t)=exp*(-∫(от 0 до1)z(t)dt) ,

T= ∫(от 0 до бесконечности) R(t)-среднее время между отказами.

Основной такой модели является уточнение поведения функции z(t). При оценке надежности аппаратуры λ -интенсивность =константе. Функция риска z(t) прямо пропорциональна числу оставшихся ошибок.

Второе предположение z(t) - прямо пропорциональна числу оставшихся ошибок: z(t)=K(N-i),

где N - неизвестное первоначальное число ошибок, i - число обнаруженных ошибок, K - некоторая неизвестная константа.

Существует модификация этой модели -Модель Шумана-относится к динамическим моделям дискретного времени, данные для которой собираются в процессе тестирования программного обеспечения в течение фиксированных или случайных интервалов времени. Предполагается, что в начальный момент компоновки программных средств в систему программного обеспечения в них имеется Е_Т шибок. С этого времени начинается отсчет времени отладки τ - включает затраты времени на выявление ошибок с помощью тестов. Модель Шумана предполагает, что тестирование проводится в несколько этапов. В конце этапа рассчитываются количественные показатели надежности, исправляются найденные ошибки, корректируются тестовые наборы и проводится следующий этап тестирования. В модели Шумана предполагается, что число ошибок в программе постоянно и в процессе корректировки новые ошибки не вносятся.

На основании полученных для каждого этапа времен и кол-ва ошибок рассчитываются параметры функции риска.

У этой модели много недостатков:

-предположения об ошибках (ошибка в тексте и результате).

-при возникновении возникающих ошибок в программу не вносятся другие.

Модель Миллса - модель строится на базе статистике. Ошибки специально вносятся в программу случайным образом. Путем тестирования программы в течение некоторого времени происходит сортировка собственных и вносимых ошибок, можно оценить первоначальное число ошибок в программе.

Предположим, что в программу внесено s ошибок, после чего начато тестирование. При тестировании обнаружено n - число собственных ошибок, v - число найденных внесенных. Тогда N=sn/v , где N-полученное значение соответствия реальных ошибок к кол-ву внесенных ошибок. Уровень значимости (мера доверия к модели) определяется: С=s/(s+k+1), k - кол-во обнаруженных собственных ошибок.