
2) Сплайны, составленные из кривых Безье

Рис. 11. Состыкованные кубические кривые Безье.
Д ля
упрощения будем считать, что параметризация
равномерная, т.е. длины отрезков, которые
пробегает параметр на каждом из участков,
равны.
ля
упрощения будем считать, что параметризация
равномерная, т.е. длины отрезков, которые
пробегает параметр на каждом из участков,
равны.
Для того чтобы рассмотреть условия на и , необходимо найти производные кривых Безье:
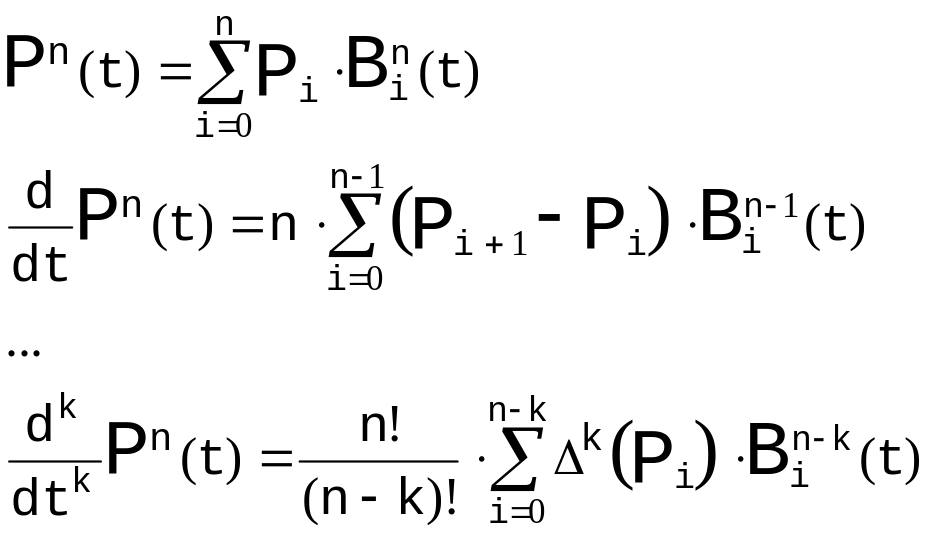 ,
где
,
где
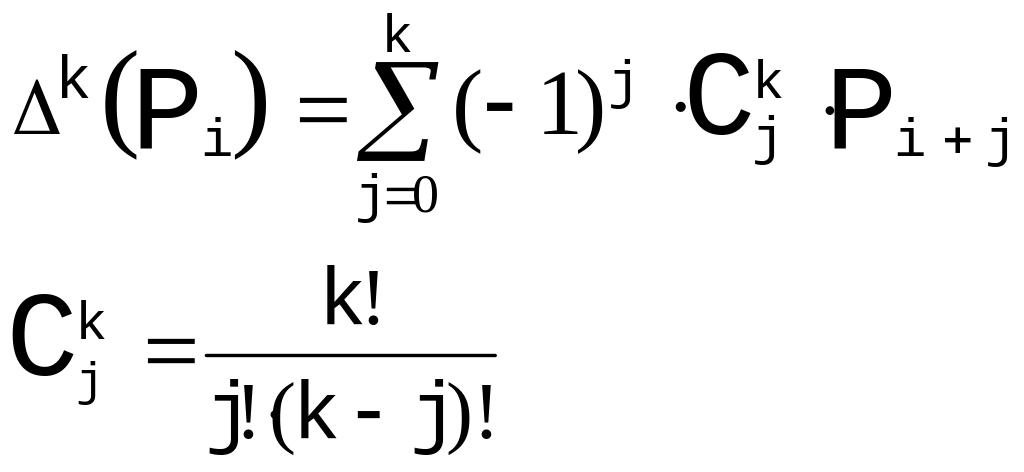
Ограничимся в рассмотрении кубическими кривыми Безье, которые более всего распространены.
1) Требование
Рис. 12. Стыковка с требованием |
Пусть заданы значение производных на концах: m0 и m1 :
Таким образом, для того, чтобы в точках стыковки производные были равны необходимо, чтобы
|
2) Требование
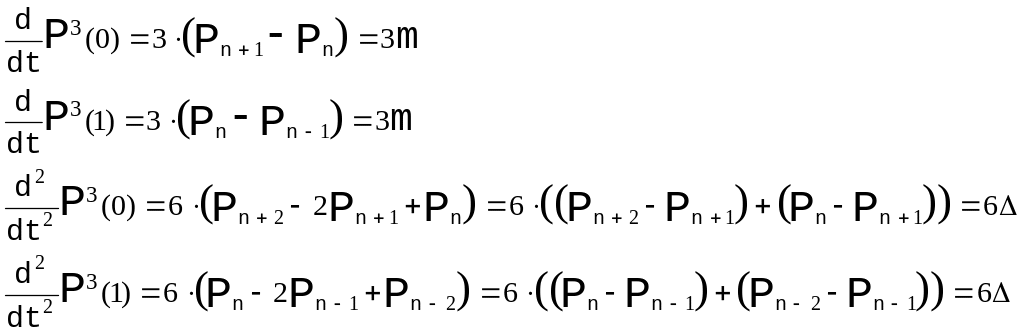
Рис. 13. Стыковка с требованием . |
Из требования
в точках стыковки получаем
Распространяя эти
рассуждения на все точки стыковки,
получаем, что для задания формы такого
сплайна достаточно задать точки
|
Рис. 14. Связь между точками для соседних сегментов. |
Замечание: Для замкнутой кривой задание краевых точек не нужно.
|
3) Сплайны, составленные из рациональных кривых Безье
Даже такие достаточно развитые средства
аппроксимации кривыми Безье не позволяют
построить окружность:![]() ,
так как sin и cos
для достаточно хорошего приближения
требуют многочленов высокой степени,
поэту вводится более широкий класс
кривых, способ построения которых связан
с представлением о проективном
пространстве.
,
так как sin и cos
для достаточно хорошего приближения
требуют многочленов высокой степени,
поэту вводится более широкий класс
кривых, способ построения которых связан
с представлением о проективном
пространстве.
Рис. 15. Рациональная кривая Безье. |
Пусть у нас есть пространственная
кривая Безье
Полученная кривая, лежащая в плоскости w=1, и называется рациональной двумерной кривой Безье.
|
Аналогичным образом можно получать
рациональные кривые Безье и в пространстве
большего числа измерений.
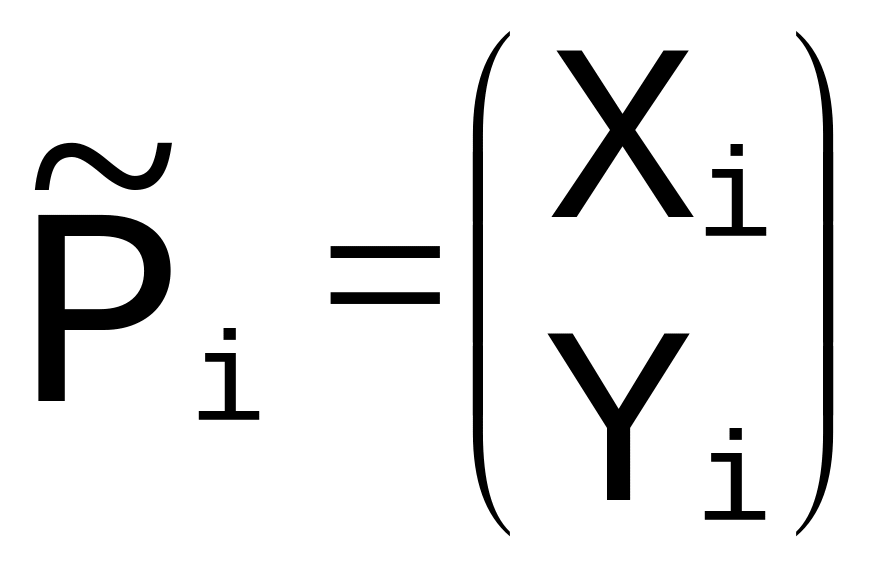 будем называть опорными точками
рациональной кривой Безье, а
будем называть опорными точками
рациональной кривой Безье, а
![]() -
весовыми функциями.
-
весовыми функциями.
Рассмотрим пример представления
окружности составленной из 3-х рациональных
кубических кривых Безье. Возьмем для
примера один из сегментов. Положим
![]() ,
а
,
а
Рис. 16. Сегмент окружности, представленный рациональной кривой Безье. |
|
Рис. 17. Изображение окружности. |
Итоговое изображение представлено на Рис. 17. Отметим, что за рамками данной лекции остались не разобранными многие важные вопросы, требующие более тщательного рассмотрения. Среди них следует отметить :
(Non-Uniform Rational B-Splines), которые в настоящее время являются фактически общепризнанным стандартом представления кривых, так как позволяют наиболее точно передавать форму кривой. 3) Аналогичную теорию можно строить и для поверхностей, что находит не меньшее, а, возможно, и большее применение в приложениях.
Всех интересующихся описанием этих вопросов, а также тех, кто хотел бы узнать более подробно о вышеизложенном материале, отсылаем к замечательной книге [Роджерс, Адамс, 2001].
|


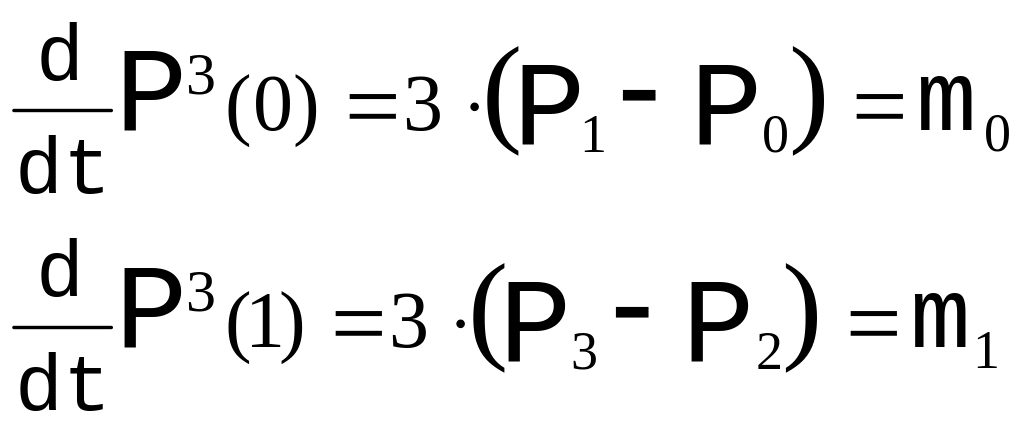





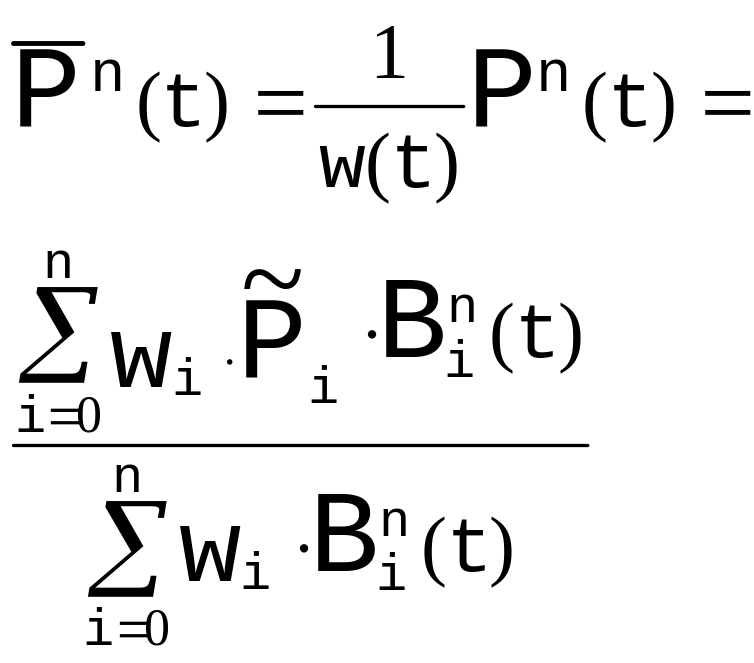 ,
где
,
где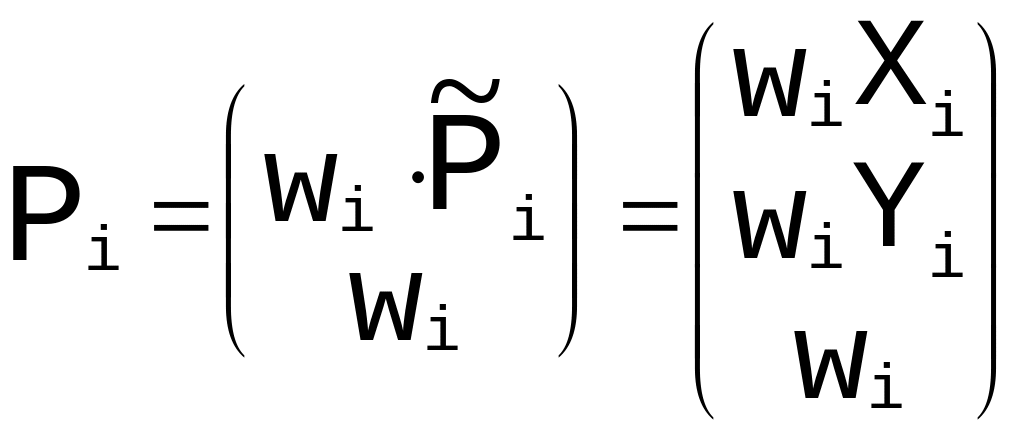 (см. Рис. 15).
(см. Рис. 15).
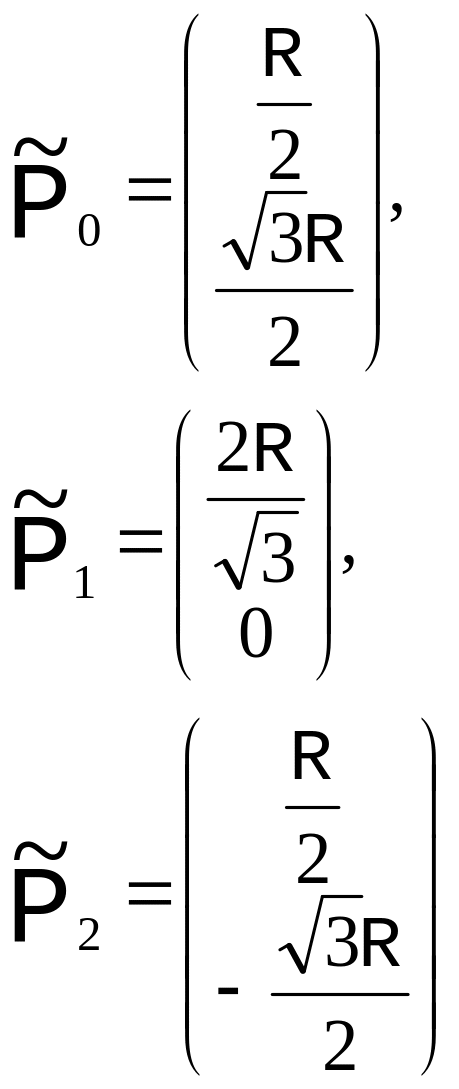 ,
где R - радиус окружности.
,
где R - радиус окружности.