Лекция 4 Изображение кривых 3

I. Аппроксимация и интерполяция.

В этой лекции будут рассматриваться вопросы построения кривых по контрольным точкам. Нас будут интересовать две задачи:

Интерполяция - построение кривой, проходящей через контрольные точки.

Аппроксимация - приближение кривой (не обязательно проходит точно через данные точки, но удовлетворяет некоторому заданному свойству относительно этих точек).

II. Интерполяция.

Постановка задачи:

Рис. 1. Постановка задачи.

Дано: . i  . Построить функцию f(x), удовлетворяющую этому условию.

1. Интерполяционный многочлен Лагранжа

; ;

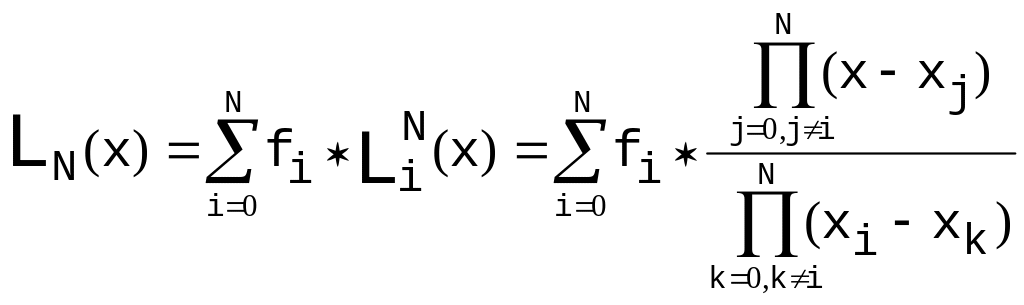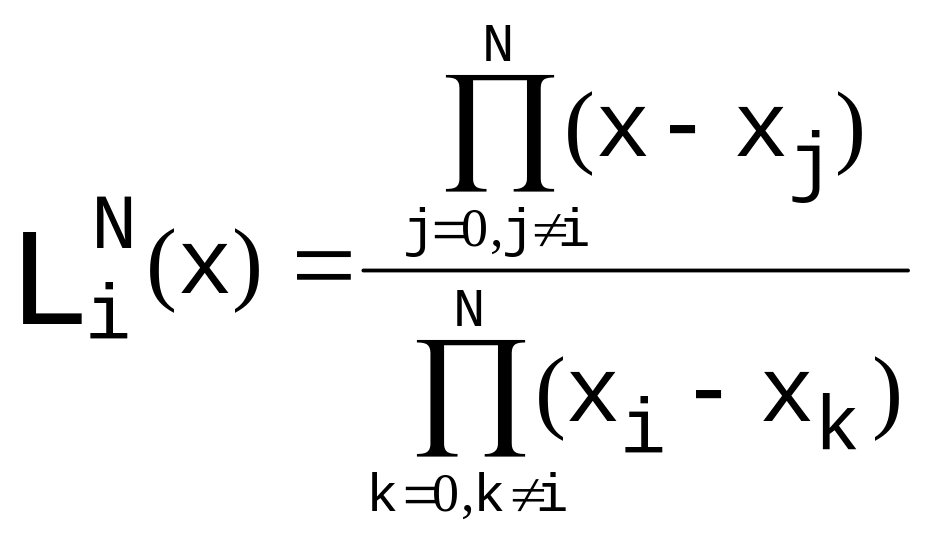Получаем непрерывную функцию, проходящую через все точки.

Минусы:

1. Требует значительного объема вычислений для нахождения значения функции в произвольной точке.

2. Неопределенное поведение построенной функции между узлами, в частности можно привести следующие результаты:

1916 Бернштейн :

1925 Рунге :

Далее будем рассматривать интерполирующие функции, которые задаются отдельно на каждом отрезке , что позволяет лучше учитывать локальное поведение требуемой функции и избежать громоздких вычислений (так как на каждом из отрезков интерполирующая функция имеет по возможности простой вид).

2) Кусочно-линейная интерполяция

Рис. 2. Кусочно-линейная интерполяция.

Интерполяция следующей кусочно-линейной функцией: Класс

3) Кубическая интерполяция Эрмита

Рис. 3. Кубическая интерполяция Эрмита.

Пусть заданы следующие условия: , тогда для каждого i будем искать искомую функцию в виде . Подставив эту функцию в уравнения условий получим линейную невырожденную систему из 4 уравнений с 4 неизвестными (a,b,c и d), т.е. решение существует и единственно. Класс

Проблемы:

1. Непонятно откуда брать значения производных.

2. Хотелось бы , а не только

4) Сплайны

Сплайн - кусочный полином степени K с непрерывной производной степени K-1 в точках соединения сегментов.

Далее нас будут интересовать кубические сплайны.

Понятие сплайна пришло из машиностроения, где сплайном называли гибкую линейку, закрепив которую в нужных местах, добивались плавной кривой, которую затем чертили по этой линейке (см. Рис. 4) Форма такой линейки, если ее рассматривать как функцию y(x), будет удовлетворять уравнению Эйлера-Бернулли: ,где M(x) - момент изгиба вдоль рейки, E - модуль Юнга. зависящий от свойств материала рейки, I - момент инерции, определяемый формой кривой. Если мы фиксируем некоторые точки подпорками, то момент изгиба на каждом отрезке меняется по линейному закону: M(x) = A*x + B , подставляя в исходное уравнение получаем: , дважды интегрируя получаем уравнение кривой на данном

Рис. 4. Сплайн.

отрезке: ; таким образом форма физического сплайна описывается кусочным кубическим полиномом. Теперь рассмотрим задачу построения системы таких кубических полиномов для всего отрезка

1. Для N отрезков имеем 4N коэффициентов: 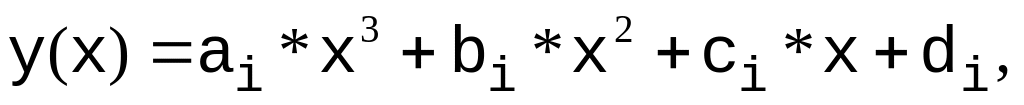для ;

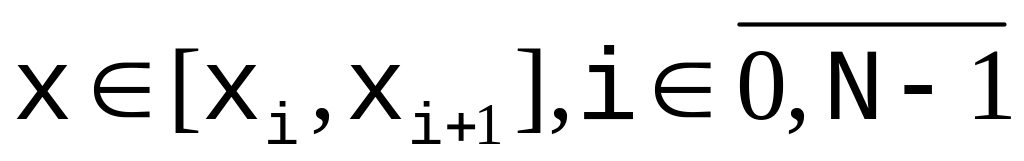2. Условия ( i  ) дают 2N уравнений;

3. Требование в точках 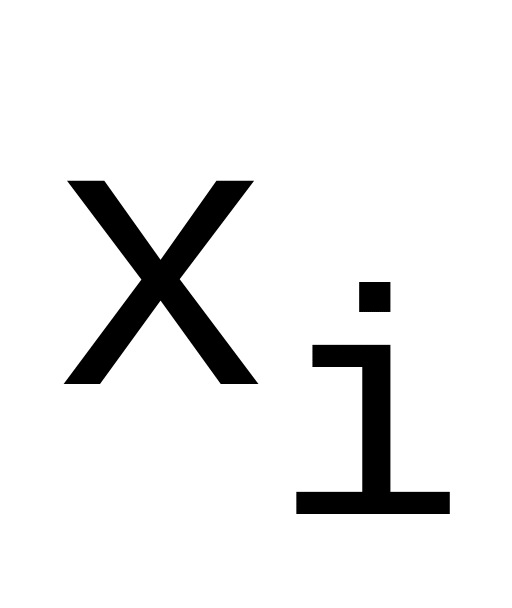( i 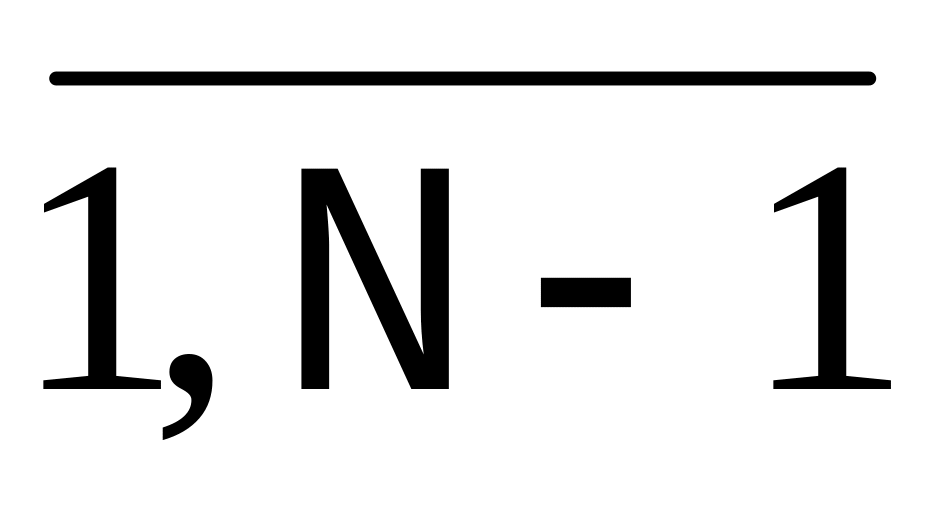 ) дает N-1 уравнений;

4. Требование в точках ( i  ) дает N-1 уравнений.

Итого имеем 4N-2 уравнения; для того чтобы система была определенной, необходимы еще 2 уравнения; их можно вывести, например, из заданных значений производных на границах или или из условия периодичности. При корректно заданных условиях линейная относительно система имеет единственное решение. Подробнее смотри в [Роджерс, Адамс, 2001].
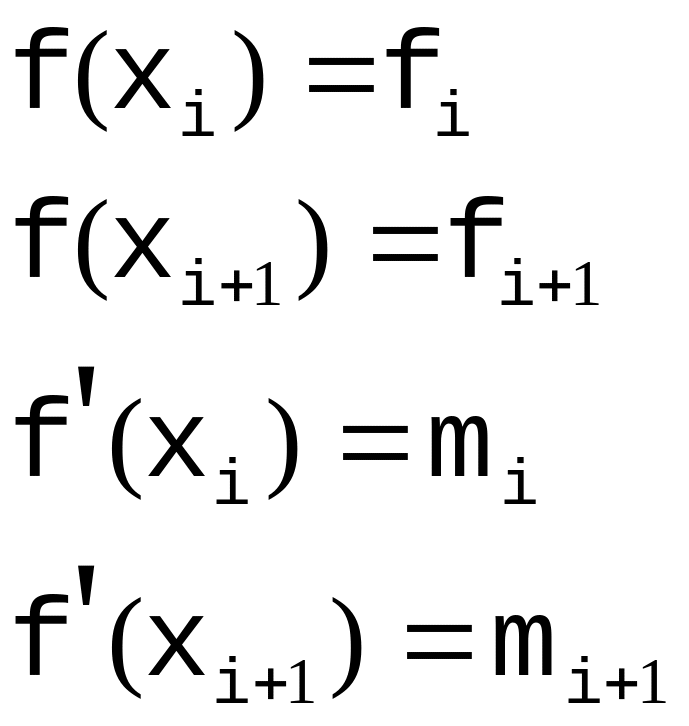