3.3 Сплайн-квадратура

Ана­ло­гично ин­тер­по­ля­ци­он­ным мно­гочле­нам, сплайн мож­но ис­поль­зо­вать для по­строе­ния квад­ра­тур­ных фор­мул с це­лью при­бли­жен­но­го вычис­ле­ния оп­ре­де­лен­ных ин­те­гра­лов.

Ин­тег­ри­руя сплайн, за­пи­сан­ный в фор­ме (13), ви­де, лег­ко по­лучить фор­му­лу

(22)

для n+1 уз­лов A=x₀x₁...x_n=B на от­рез­ке ин­тег­ри­ро­ва­ния [A,B]. Од­на­ко, эту фор­му­лу мож­но су­ще­ст­вен­но уп­ро­стить, за­пи­сав сплайн в ви­де (17). То­гда для ин­те­гра­ла на эле­мен­тар­ном от­рез­ке по­лучаем:

.

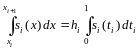Учиты­вая, что , име­ем:

.

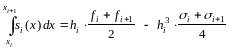Весь ин­те­грал на от­рез­ке [A,B] по­лучает­ся сум­ми­ро­ва­ни­ем по эле­мен­тар­ным от­рез­кам:

. (23)

Та­ким об­ра­зом, тре­бу­ют­ся толь­ко значения функ­ции f_i и ко­эф­фи­ци­ен­ты c_i, вычис­ляе­мые биб­лио­течной про­це­ду­рой SPLINE. В случае рав­но­от­стоя­щих точек (h₀=h₁=...=h_n1=h=(BA)n) эту фор­му­лу мож­но еще бо­лее уп­ро­стить.

Приложение. Текст библиотечного модуля splinunt на языке Паскаль для интерполяции кубическими сплайнами.

{====================} UNIT SplinUNT; {======================}

{ В этот модуль включены подпрограммы SPLINE и SEVAL из книги

Форсайт Дж., Малькольм М., Моулер К., Машинные методы математи-

ческих вычислений: Пер. с анг.- М.: Мир, 1980. с. 91-94.

Для повышения точности интерполяции используется арифметика

с плавающей точкой, определяемая типом

RealType = double

Если Ваш компьютер не имеет арифметического сопроцессора, и

Вы хотите несколько увеличить скорость вычислений ценой ухуд-

шения точности, а также во всех других случаях, когда необходи-

мо сменить базовый вещественный тип (например, в целях экономии

памяти), Вы должны желаемым образом изменить определение вещес-

твенного типа, например: type RealType = real;

}

{-------------------------------------------------------------}

INTERFACE

{$N+,E+}

type

RealType = double; { базовый вещественный тип }

RealTypeArray =

array [1..(2*MaxInt) div Sizeof(RealType)] of RealType;

procedure Spline (N : word; var XI, YI, BI, CI, DI);

{

Вычисляются коэффициенты B[i], C[i] и D[i], i = 1..N

для кубического интерполяционного сплайна вида

S(X) = Y[i] + B[i]*(X-X[i]) + C[i]*(X-X[i])^2 + D[i]*(X-X[i])^3

для X[i] <= X <= X[i+1].

ВХОДНАЯ ИНФОРМАЦИЯ:

N - число заданных точек или узлов (N >= 2);

X - абсциссы узлов в строго возрастающем порядке;

Y - ординаты узлов.

ВЫХОДНАЯ ИНФОРМАЦИЯ:

B, C, D - массивы коэффициентов сплайна, записанного в указанной

выше форме.

Если обозначить дифференцирование символом ', то

Y[i] = S(X[i]);

B[i] = S'(X[i]);

C[i] = S''(X[i])/2;

D[i] = S'''(X[i])/6 (правосторонняя производная).

С помощью сопровождающей функции SEVAL можно вычислять значения

сплайна.

}

{-------------------------------------------------------------}

function Seval (N : word; var U : RealType;

var XI, YI, BI, CI, DI) : RealType;

{

Эта функция вычисляет значение кубического сплайна:

Seval = Y[i]+B[i]*(U-X[i])+C[i]*(U-X[i])**2+D[i]*(U-X[i])**3

где X[i] <= U <= X[i+1]. Используется схема Горнера.

Если U < X[1], то берется значение i = 1;

если U > X[N], то i = N.

ВХОДНАЯ ИНФОРМАЦИЯ:

N - число заданных точек (N >= 2);

U - абсцисса, для которой вычисляется значение сплайна;

X, Y - массивы заданных абсцисс и ординат;

B, C, D - массивы коэффициентов сплайна, вычисленные

процедурой Spline.

Если по сравнению с предыдущим вызовом Seval значение U не

находится в том же интервале, то для отыскания нужного ин-

тервала используется двоичный поиск.

}

{-------------------------------------------------------------}

IMPLEMENTATION

procedure Spline (N : word; var XI, YI, BI, CI, DI);

var

X : RealTypeArray absolute XI;

Y : RealTypeArray absolute YI;

B : RealTypeArray absolute BI;

C : RealTypeArray absolute CI;

D : RealTypeArray absolute DI;

T : RealType;

i : integer;

begin { Spline }

if N < 2 then Exit;

if N = 2 then begin

B[1] := (Y[2] - Y[1]) / (X[2] - X[1]);

C[1] := 0;

D[1] := 0;

B[2] := B[1];

C[2] := 0;

D[2] := 0

end

else begin

{ Формирование трехдиагональной системы линейных уравнений:

B = диагональ, D = наддиагональ, C = правые части. }

D[1] := X[2] - X[1];

C[2] := (Y[2] - Y[1]) / D[1];

for i := 2 to N-1 do begin

D[i] := X[i+1] - X[i];

B[i] := 2 * (D[i-1] + D[i]);

C[i+1] := (Y[i+1] - Y[i]) / D[i];

C[i] := C[i+1] - C[i]

end;

{ Граничные условия. Третьи производные в точках X[1] и X[N]

оцениваются с помощью разделенных разностей. }

B[1] := -D[1];

B[N] := -D[N-1];

if N = 3 then begin

C[1] := 0;

C[N] := 0

end

else begin

C[1] := C[3]/(X[4]-X[2]) - C[2]/(X[3]-X[1]);

C[N] := C[N-1]/(X[N]-X[N-2]) - C[N-2]/(X[N-1]-X[N-3]);

C[1] := C[1] * sqr(D[1])/(X[4]-X[1]);

C[N] := -C[N] * sqr(D[N-1])/(X[N]-X[N-3])

end;

{ Прямой ход метода Гаусса }

for i := 2 to N do begin

T := D[i-1]/B[i-1];

B[i] := B[i] - T*D[i-1];

C[i] := C[i] - T*C[i-1]

end;

{ Обратная подстановка }

C[N] := C[N]/B[N];

for i := N-1 downto 1 do C[i] := (C[i] - D[i]*C[i+1]) / B[i];

{ В C[i] теперь хранится значение Sigma(i), определяемое в книге:

Дж.Форсайт, М.Малькольм, К.Моулер, Машинные методы математических

вычислений. }

{ Вычисление коэффициентов сплайна B, C и D }

B[N] := (Y[N]-Y[N-1])/D[N-1] + D[N-1]*(C[N-1]+2*C[N]);

for i := 1 to N-1 do begin

B[i] := (Y[i+1]-Y[i])/D[i] - D[i]*(C[i+1]+2*C[i]);

D[i] := (C[i+1]-C[i])/D[i];

C[i] := 3*C[i]

end;

C[N] := 3*C[N];

D[N] := D[N-1]

end { N <> 2 };

end { Spline };

{-------------------------------------------------------------}

function Seval (N : word; var U : RealType;

var XI, YI, BI, CI, DI) : RealType;

var

X : RealTypeArray absolute XI;

Y : RealTypeArray absolute YI;

B : RealTypeArray absolute BI;

C : RealTypeArray absolute CI;

D : RealTypeArray absolute DI;

DX : RealType;

j, k : integer;

const

i : integer = 1;

begin { Seval }

if i >= N then i := 1;

if (U < X[i]) or (U > X[i+1]) then begin { Двоичный поиск }

i := 1;

j := N+1;

repeat

k := (i+j) div 2;

if U < X[k] then j := k else i := k

until j <= i+1

end;

{ Вычисление сплайна }

DX := U - X[i];

Seval := Y[i] + DX*(B[i] + DX*(C[i] + DX*D[i]))

end { Seval };

{=================} END. { Unit SplinUNT } {==================}

 Употребляется также термин «интерполянт».

 Мно­гочлен, за­пи­сан­ный в фор­ме (9), час­то на­зы­ва­ют ин­тер­по­ля­ци­он­ным мно­гочле­ном Ла­гран­жа, хо­тя на са­мом де­ле это не осо­бый вид мно­гочле­на, а лишь од­на из воз­мож­ных форм пред­став­ле­ния един­ст­вен­но­го су­ще­ст­вую­ще­го ин­тер­по­ля­ци­он­но­го мно­гочле­на дан­ной сте­пе­ни.

1. Ahlberg H. J., Nilson E. N., Walsh J. L. The theory of splines and their application. N.-Y.: Academic Press, 1967. Рус­ский пе­ре­вод: Ал­берг Дж., Ниль­сон Э., Уолш Дж. Тео­рия сплай­нов и ее при­ло­же­ния. М.: Мир, 1972.

2. Стечкин С. Б., Субботин Ю. Н. Сплай­ны в вы­чис­ли­тель­ной ма­те­ма­ти­ке. М.: Наука, 1976.

3. Завьялов Ю. С., Квасов Б. И., Мирошниченко В. Л. Ме­то­ды сплайн-функ­ций. М.: Наука, 1980.

4. Форсайт Дж., Малькольм М., Моулер К. Ма­шин­ные ме­то­ды ма­те­ма­ти­чес­ких вы­чис­ле­ний. М.: Мир, 1980. Гл. 4.

11