Вариант 8
Найти интегралы, используя свойство линейности:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
Найти интегралы методом подстановки:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
3. Интегрирование по частям:
1)
2)
3)
Найти интегралы:
1)
2)
3)
Найти интегралы от рациональных дробей:
1)
2)
3)
Вычислить интегралы:
1)
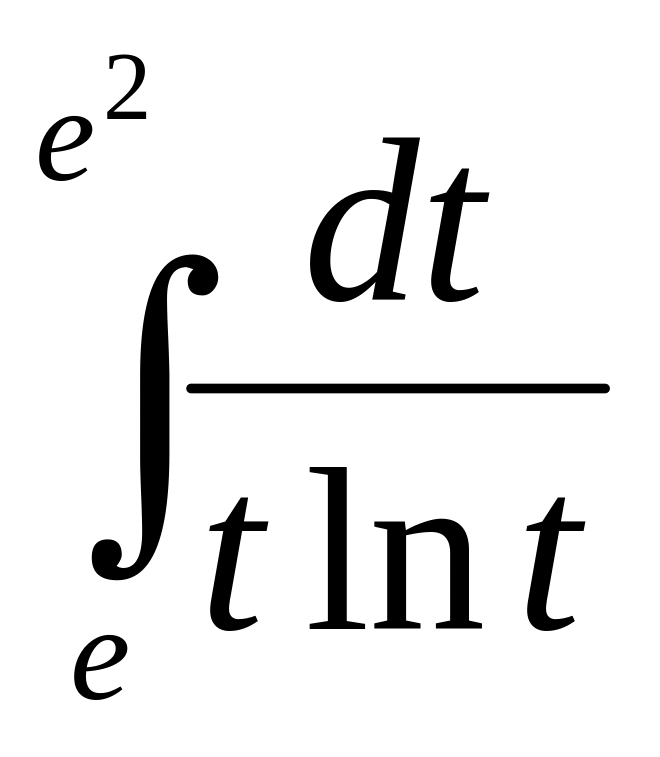2)
3)
Вычислить площадь плоской фигуры, ограниченной линиями:
а)
y= -
б) y= Sin x, y= Cos x, x=0
Вычислить двойные интегралы:
а)
б)
в)
D:
D:
D:
Перейти к полярным координатам и в пункте б) вычислить интеграл:
а)
б)
D:
D:
Решить дифференциальные уравнения 1-го порядка:
1)
2)
3)
4)
5)
6)
7) xdy+ylnxdx=ylnydx, y(1)=1
8) SinyCosxdy=CosySinxdx
9)
10)
Решить линейные дифференциальные уравнения с постоянными коэффициентами:
а) однородные: б) неоднородные:
1
2
3
Вариант 9
1.Найти интегралы, используя свойство линейности:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
2.Найти интегралы методом подстановки:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
3.Интегрирование по частям:
1)
2)
3)
4.Найти интегралы:
1)
2)
3)
5.Найти интегралы от рациональных дробей:
1)
2)
3)
6.Вычислить интегралы:
1)
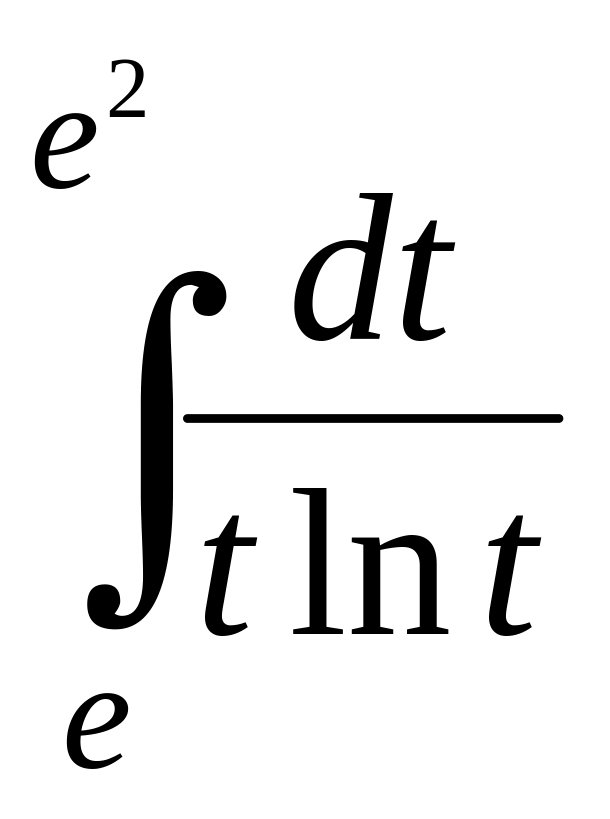2)
3)
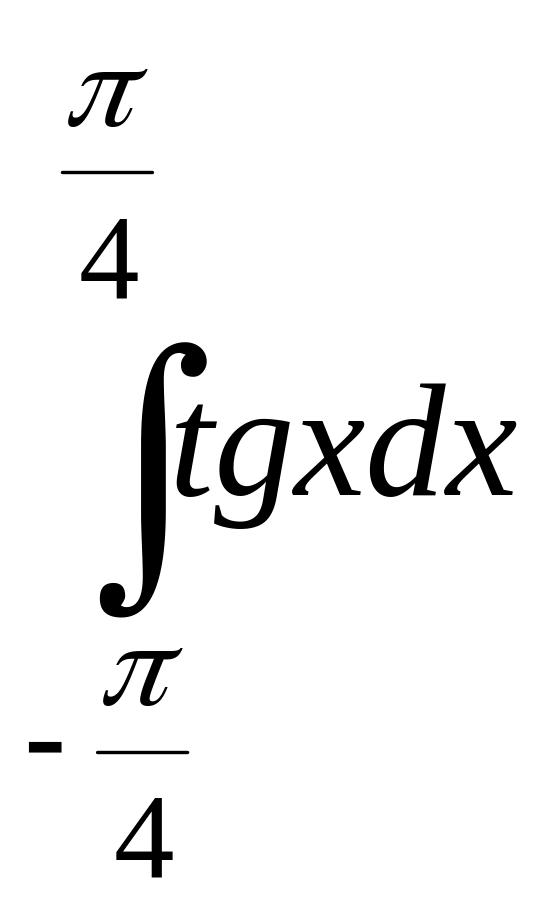
7.Вычислить площадь плоской фигуры, ограниченной линиями:
а)
б)
8.Вычислить двойные интегралы:
а б в
D:
D:
D:
9.Перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а) б)
D:
D:
10.Решить дифференциальные уравнения 1-го порядка:
1 
2 
3 
4 
5 
6 
7 
8 
9 
10
11.Решить линейные дифференциальные уравнения с постоянными коэффициентами:
а) однородные: б) неоднородные:
1. 1.
2.
2.
3. 3.
Вариант 10
1. Найти интегралы, используя свойство линейности:
1).
2).
3).
4).
5).
6).
7).
8).
9).
10).
2. Найти интегралы методом подстановки:
1).
2).
3).
4).
5).
6).
7).
8).
9).
10).
11).
12).
3. Интегрирование по частям:
1).
2).
3).
4. Найти интегралы:
1).
2).
3).
5. Найти интегралы от рациональных дробей:
1).
2).
3).
6.
Вычислить интегралы:
1).
2).
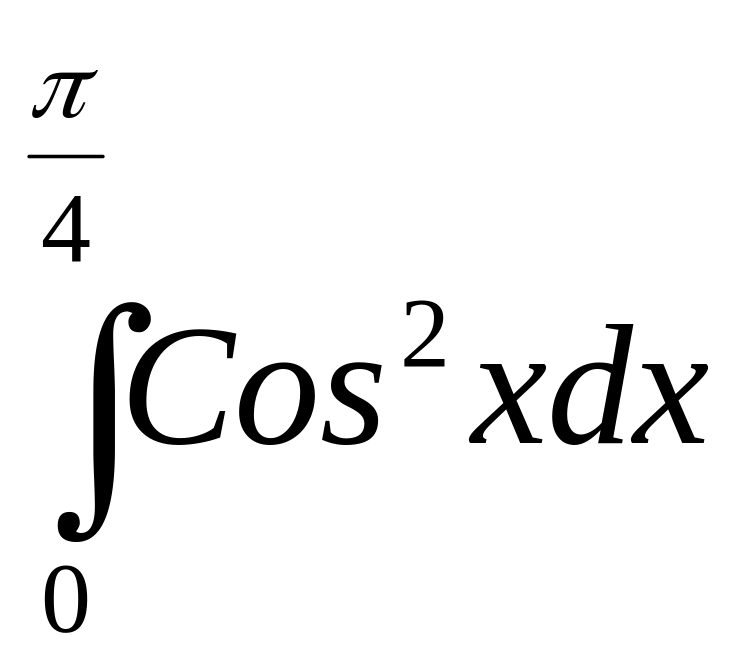3).
7.
Вычислить площадь плоской фигуры,
ограниченной линиями:
а).
и осью абсцисс
б).
8.
Вычислить двойные
интегралы:
а б в
9. Перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а)
б)
10. Решить дифференциальные уравнения 1-го порядка:
11. Решить линейные дифференциальные уравнения с постоянными коэффициентами:
а). однородные: б). неоднородные:
1.
1.
2.
2.
3.
3.
