Теоретический материал

Для определения объемов штабелей навалочного груза, имеющих правильную геометрическую форму, можно использовать три метода решения задач. Первый метод заключается в разложении сложных геометрических фигур на простейшие (рис. 3.1). В дальнейшем используются следующие обозначения:

радиус конуса по нижнему и верхнему основаниям, м;

сторона квадрата основания пирамиды, ширина клина, м;

длина ширина и высота штабеля соответственно, м;

диаметр конуса по нижнему и верхнему основаниям, м;

, b – длина и ширина верхнего основания штабеля, м;

угол естественного откоса;

окружность основания штабеля, м.

Индексы: к – конус, п – пирамида, пр – призма, кл – клин, об – обелиск

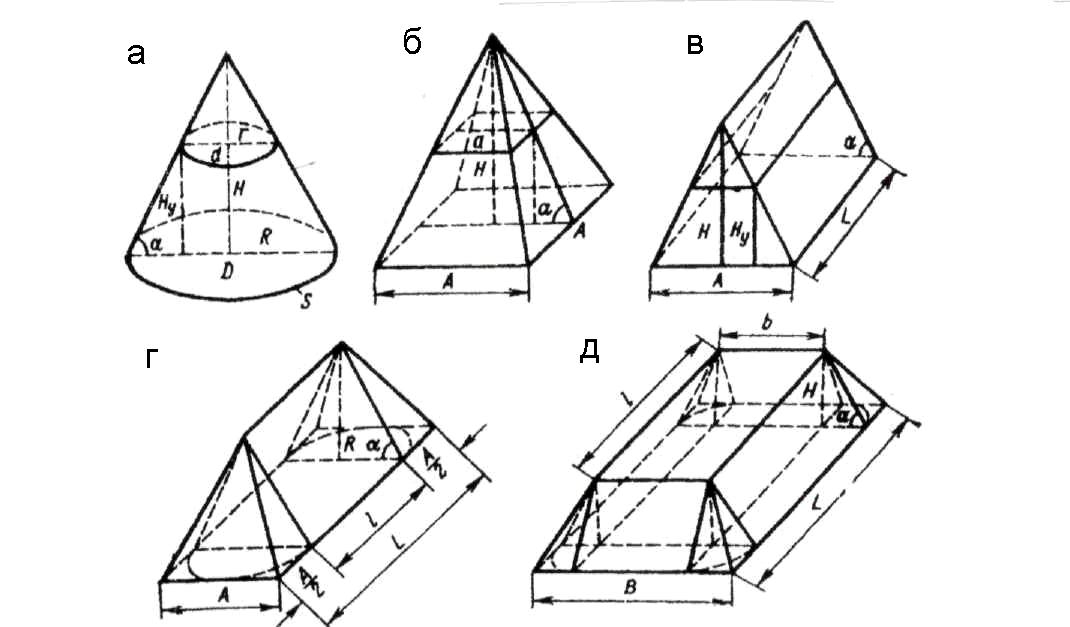
Рис. 3.1. Формы штабелей навалочных грузов:

а) конус; б) пирамида; в) призма; г) клин; д) обелиск

Формулы для расчетов

Конус	Пирамида		Призма
Клин		Обелиск

Общими для этих фигур являются соотношения:

Второй метод – метод коэффициентов формы – заключается в том, что объем штабелей правильной геометрической формы определяется по формуле

где – коэффициент формы. Он разный для разных фигур.

Объем конуса:

Объем пирамиды:

Объем призмы:

Объем клина:

Объем обелиска:

Для определения объема штабелей правильной формы Л.П. Андроновым предложена номограмма (рис. 3.2).

tg

Рис. 3.2. Номограмма для определения объема штабелей навалочных грузов

Она состоит из девяти логарифмических шкал на пяти осях и дает возможность определить все остальные элементы, если известны хотя бы два, например, угол естественного откоса и периметр основания конуса .

Шкалы 5, 6, 8 предназначены для определения объема призмы.

Для определения объема конуса измеренные значения диаметра (или окружности основания) и угла откладывают на шкалах 1(2) и 9, соединяют эти точки прямой и со шкалы 4 снимают его значение. Если значения А или S выходят за пределы шкал, то их уменьшают в 10 раз, а результат на шкале 4 увеличивают в 10³ раз.

Объем пирамиды определяют аналогично (по шкалам 1, 9 и 3). Для определения объема призмы откладывают измеренные значения на шкалах 1 и 9, соединяют эти точки прямой, пересечение которой со шкалой 5 дает значение С. Точка пересечения прямой, проведенной между значением на шкале С и значением L, отложенным на шкале 8, со шкалой 6 дает значение объема V_пр призмы. Если значение величины выходит за пределы шкалы 8, его уменьшают в 10 (100) раз, соответственно увеличивают значение V_пр.

При определении объема клина по значениям А и находят объем V_п пирамиды (или конуса, если основание круглое) и значение величины С, по С и L – объем V_пр призмы. Объем клина равен сумме объемов пирамиды V_п (конуса V_к) и призмы V_пр .

Объем обелиска можно представить как сумму объемов параллелепипеда l b Н (см. рис. 3.1, д), призмы сечением С, длиной (L + B) и пирамиды (конуса, если основание круглое), высота которой равна высоте обелиска. Для определения V_об надо знать значения L и l, В и b, угол либо Н. По разности соответствующих сторон оснований определяют сторону основания пирамиды (диаметр конуса), по длине и ширине основания – длину призмы. Значения величин Н, С, V_п (V_к) находят по номограмме (см. рис. 3.2) на шкалах А и .

На шкале 1 откладывают значение А = В – в, на шкале 9 – значение . Соединив полученные точки прямой, получают на шкале 3 значение V_п, на шкале 5 – значение С, на шкале 7 – значение высоты Н обелиска. На шкале 8 откладывают значение L. Соединив полученную точку с точкой С на шкале 6, снимают значение объема V_пр призмы. Объем обелиска V_об = V_пр + V_п + ℓb H.