Исследование физических процессов, приводящих к уравнениям параболического типа
Вывести уравнение для процесса нагревания однородной тонкой проволоки постоянным электрическим током, если на ее поверхности происходит теплообмен с окружающей средой.
Вывести уравнение диффузии в среде, равномерно движущейся в направлении оси со скоростью
.
Рассмотреть случай одной независимой
переменной.Исходя из уравнений Максвелла, предполагая
,
и пренебрегая токами смещения, показать,
что в однородной проводящей среде
составляющая электромагнитного поля
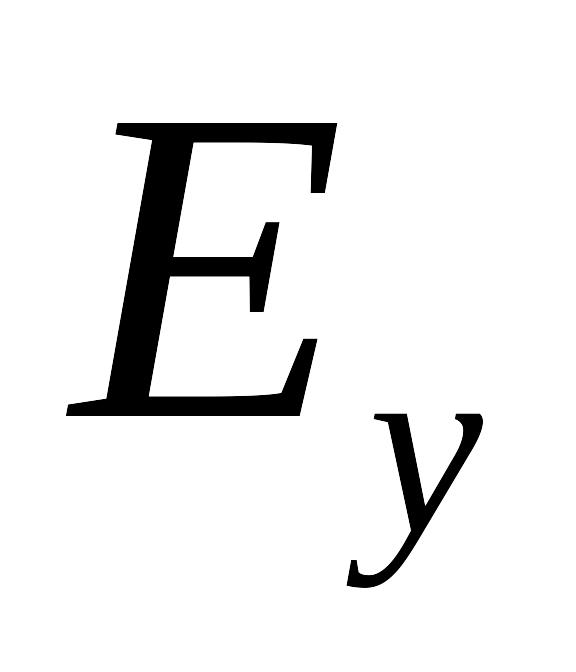удовлетворяет уравнению
где
– проводимость среды,
– скорость света. Вывести уравнения
для
.
Стержень
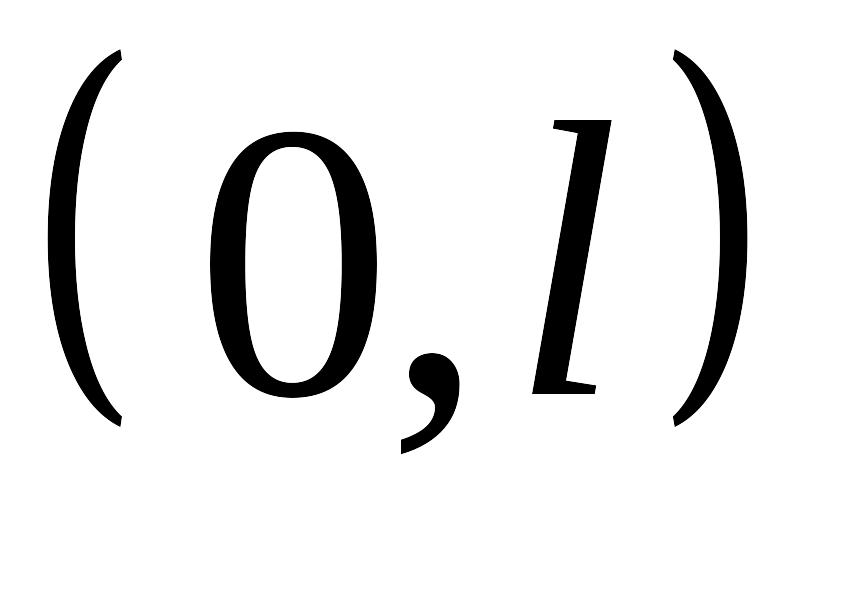составлен из двух однородных кусков
одинакового поперечного сечения,
соприкасающихся в точке
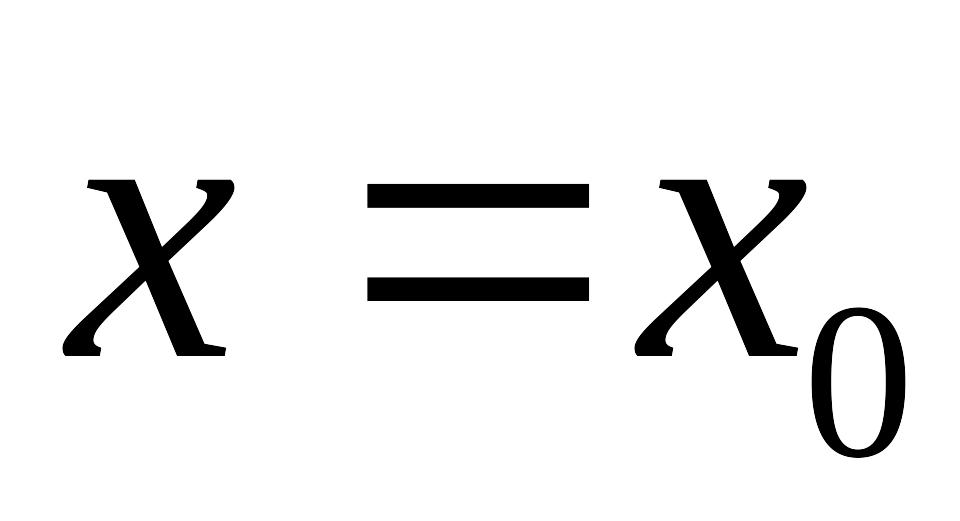и обладающих характеристиками
,
и
,
соответственно. Найти установившуюся
температуру в таком стержне (тепловые
волны), если один конец стержня (
)
поддерживается при нулевой температуре,
а температура второго меняется
синусоидально во времени.Левый конец составного стержня из задачи 26 поддерживается при температуре, равной нулю, а правый – при температуре
,
начальная же температура стержня
равна нулю. Найти температуру
стержня в регулярном режиме (первый
член разложения).Полуограниченный стержень с теплоизолированной боковой поверхностью был равномерно нагрет до температуры
(
).
Конец стержня, начиная с момента , поддерживается при температуре, равной нулю:
( )
Найти температуру стержня
и, используя систему Mathematica, построить
графики по
на интервале
функции
при
,
,
.
Указание. Для упрощения анализа ввести безразмерные переменные
,
,
.
Конец полуограниченного цилиндра в начальный момент времени открывают в атмосфере, где концентрация некоторого газа равна
.
Найти концентрацию газа в цилиндре
для
и
,
если начальная концентрация
.
Вычисляя в системе Mathematica интеграл
ошибок, установить, через какое время
в слое, отстоящем на расстояние
от конца цилиндра, концентрация газа
достигнет 95% внешней концентрации.
Найти закон движения фронта постоянной
концентрации.К концу полуограниченного стержня, начальная температура которого была равна , подводится тепловой поток
.
Найти температуру
стержня, если: а) стержень теплоизолирован
с боков; б) на боковой поверхности
стержня происходит теплообмен (по
закону Ньютона) со средой нулевой
температуры. Рассмотреть частный
случай
.Пользуясь методом отражения, построить функцию влияния мгновенного точечного источника для ограниченного стержня с теплоизолированной боковой поверхностью при граничных условиях 1-го и 2-го рода.
Неограниченный стержень составлен из двух однородных стержней, соприкасающихся в точке и обладающих характеристиками , и , соответственно. Начальная температура
Найти температуру стержня для случая, когда боковая поверхность теплоизолирована.