2. Теория потенциалов

27. Найти объемный потенциал сферы при постоянной плотности .

Указание. Решить уравнения вне сферы и внутри сферы и решения сопрягать на поверхности сферы.

28. Найти потенциал простого слоя, распределенного с постоянной плотностью на сфере.

Указание. Искать решение уравнения вне и внутри сферы и воспользоваться для сопряжения условиями разрыва производной потенци­ала простого слоя.

3. Физические приложения эллиптических уравнений

29. Написать разложение по сферическим функциям плотности поверх­ностных зарядов, индуцированных на проводящей сфере точечным зарядом.

30. Решить задачу о поляризации диэлектрического шара в поле то­чечного заряда.

31. Вычислить гравитационный потенциал плоского диска. Сравнить с асимптотическим представлением гравитационного потенциала на больших расстояниях.

32. Вычислить магнитный потенциал кругового тока.

33. Решить задачу о возмущении плоскопараллельного электрического поля идеально проводящей сферой. Решить задачу для абсолютно непрово­дящей сферы.

Индивидуальные задания для самостоятельной работы

Задача 1. В соответствии с Вашим вариантом найдите функцию Грина в одной из следующих областей:

1. в полупространстве ;

2. в двугранном угле , ;

3. в октанте , , ;

4. в шаре ;

5. в полушаре , ;

6. в четверти шара , , ;

7. в одной восьмой шара , , , ;

8. между двумя параллельными плоскостями и .

Задача 2. В соответствии с Вашим вариантом найдите методом функций Грина решение задачи Дирихле:

, ;

для следующих и ( – произвольная точка области, в которой ищется решение; – точка на границе):

1. и непрерывны и ограничены;

2. , ;

3. , ;

4. , ;

5. , ;

6. , ;

7. ,

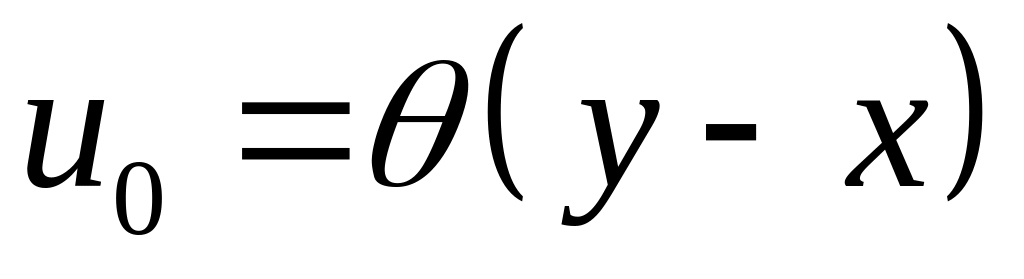Контрольные вопросы

1. Фундаментальные решения уравнения Лапласа на плоскости.

2. Фундаментальные решения уравнения Лапласа в пространстве.

3. Физический смысл фундаментальных решений.

4. Формула Грина.

5. Интегральная формула Грина.

6. Гармонические функции. Свойства гармонических функций.

7. Общая характеристика решения краевых задач методом функций Грина.

8. Физический смысл функции Грина.

9. Задача Дирихле для полупространства: постановка, решение методом функций Грина, физическая интерпретация результата.

10. Задача Дирихле для шара: постановка, решение методом функций Грина, физическая интерпретация результата.

11. Третья краевая задача для круга. Решение методом разделения переменных.

12. Объемный потенциал: физическая интерпретация и свойства.

13. Логарифмический потенциал: физическая интерпретация и свойства.

14. Поверхностные потенциалы: физическая интерпретация и свойства.

Литература

1. Конспект лекций.

2. Тихонов А.Н., Самарский А.А. Уравнения математической физики: Учебное пособие для вузов. – М.: Изд-во МГУ, 1999. – 798 с.

3. Владимиров В.С., Жаринов В.В. Уравнения математической физики: Учебник для ВУЗов. – М.: Физматлит, 2001. – 398 с.

4. Мартинсон Л.К., Малов Ю.И. Дифференциальные уравнения математической физики. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2002. – 367 с.

5. Боголюбов А.Н., Кравцов В.В. Задачи по математической физике. – М.: МГУ, 1998. – 350 с.

6. Сборник задач по уравнениям математической физики. / Под.ред. В.С. Владимирова –М.: Физматлит, 2001. – 288 с.

1 См.: Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. М.: Наука, 1985.