§ 3. Краевые задачи для уравнения лапласа вне круга
Рассмотрим теперь внешнюю краевую задачу
вне
круга
,
,
и регулярна на бесконечности.
Напомним,
что в двумерном случае регулярность на
бесконечности означает, что функция
имеет конечный предел при
.
Решение этой задачи можно записать в виде разложения (5.5). Но, как и для внутренней задачи, решение удобнее представить в виде
-
(5.14)
.
Коэффициенты
и
определяются из граничного условия
и вычисляются по формулам
-
(5.15)
Отдельно выпишем решения первой, второй и третьей краевых задач вне круга.
Задача Дирихле:
,
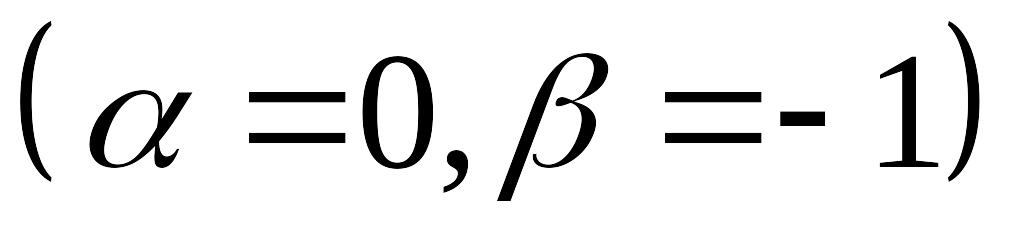(5.16)
Задача Неймана:
,
-
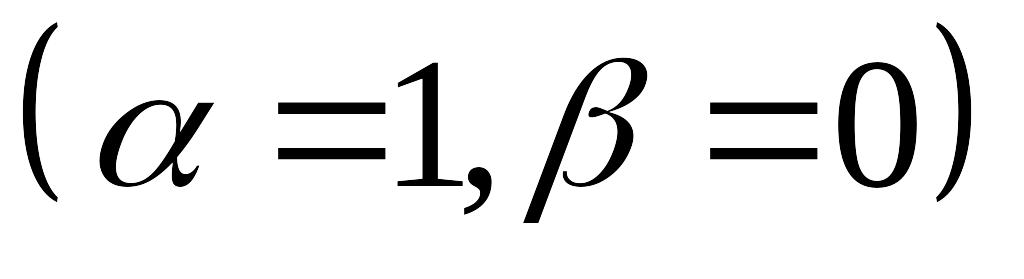,(5.17)
где – произвольная постоянная. Опять напомним, что на плоскости внешняя задача Неймана Разрешима лишь при условии
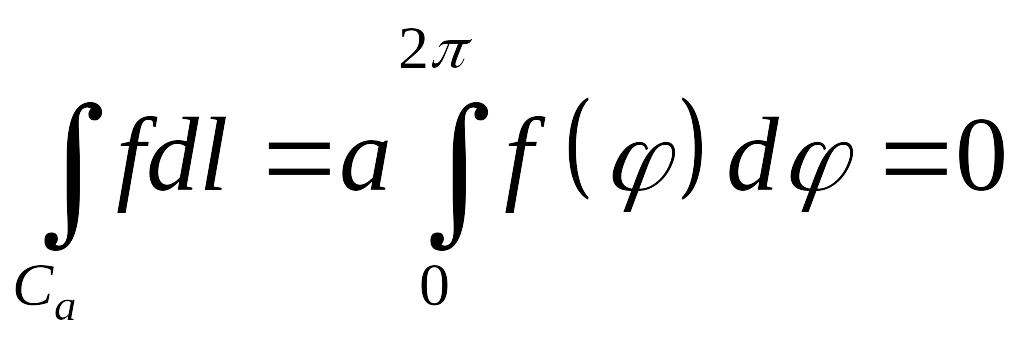
и её решение определяется с точностью до постоянного слагаемого.
Третья краевая задача:
,
-
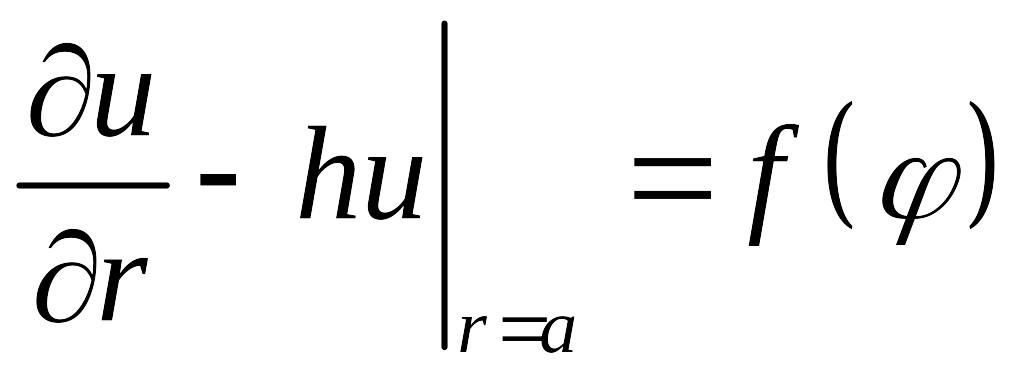
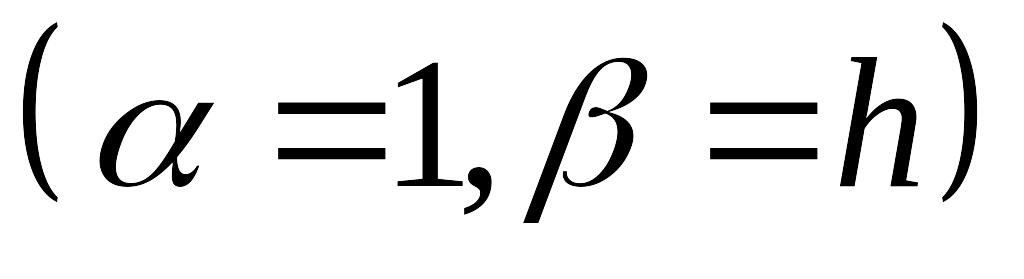,(5.18)
Коэффициенты и в разложениях (5.16) – (5.18) являются коэффициентами Фурье функции и вычисляются по формулам (5.15).
§ 4. Краевые задачи для уравнения лапласа в круговом кольце
Разберём теперь решение краевой задачи для уравнения Лапласа внутри кругового кольца.
Рассмотрим сначала задачу Дирихле
-
в кольце
,(5.19)
,
.(5.20)
Решение
этой задачи можно записать в виде
разложения по частным решениям (5.6). Но
вычисления значительно упрощаются,
если при каждом
построить систему фундаментальных
решений
уравнения
-
,(5.21)
удовлетворяющих граничным условиям
, 
.
Поскольку общее решение уравнения (5.21) имеет вид
при
,
при
,
мы,
подбирая коэффициенты
и
,
легко построим нужные решения. Они
определяются с точностью до числового
множителя, и их можно взять, например,
в виде
, 
,
, 
,
.
Построив
функции
и
,
получаем систему частных решений
уравнения Лапласа:
, 
,
,
-
,
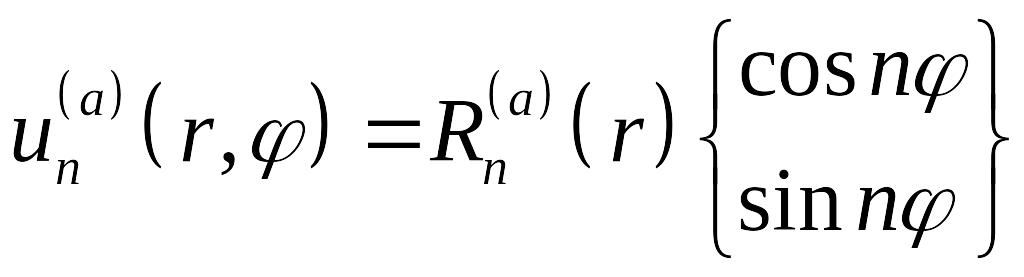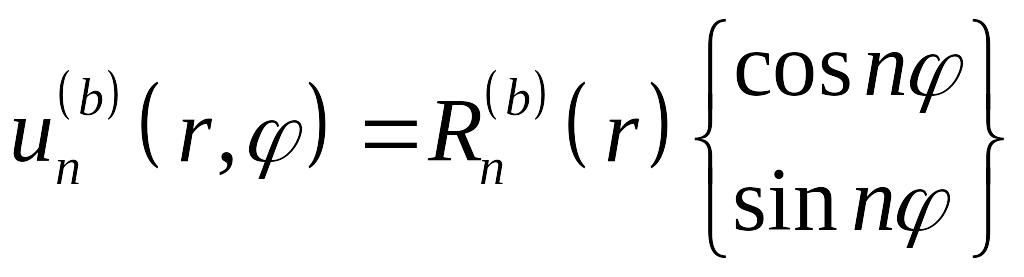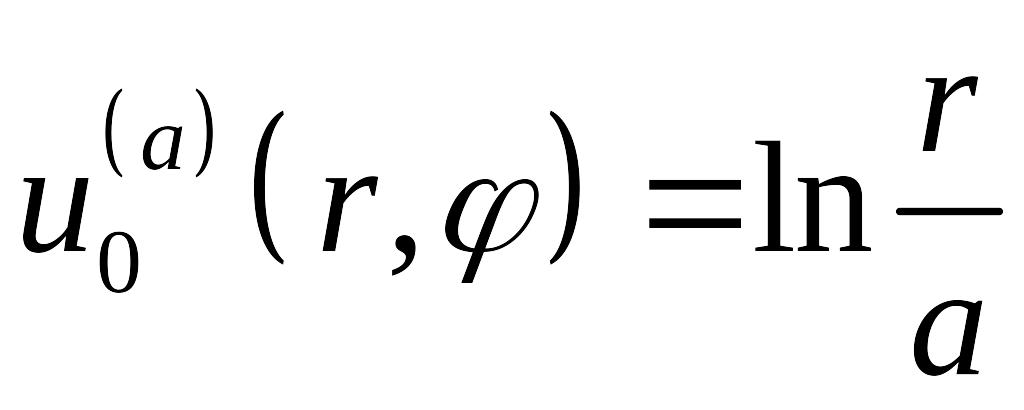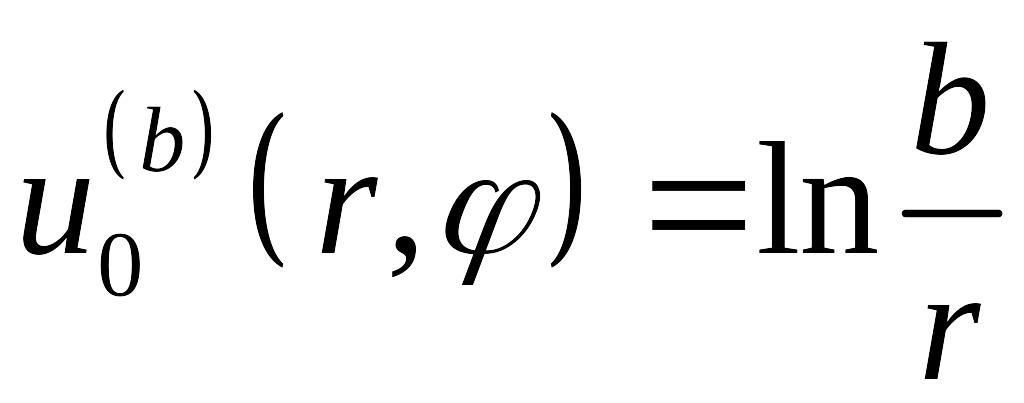,(5.22)
ограниченных внутри кольца и удовлетворяющих граничным условиям
-
,
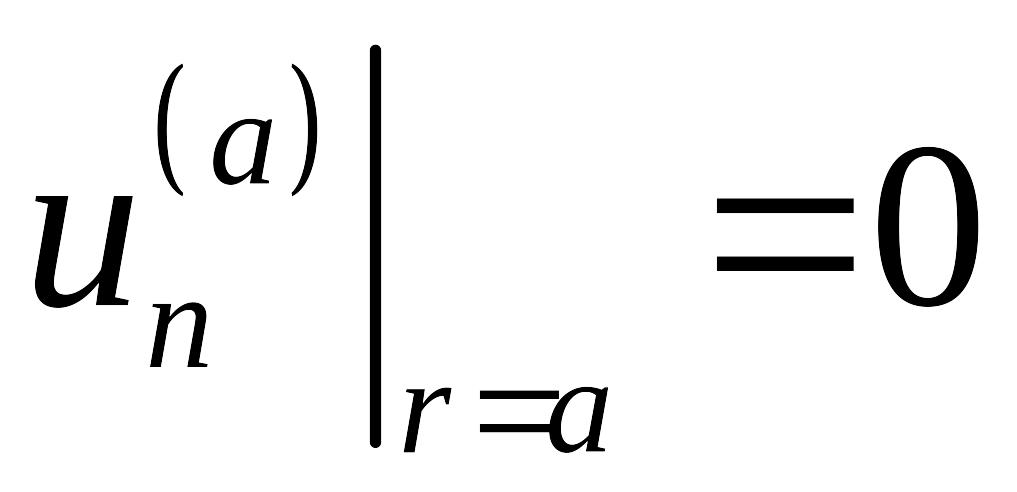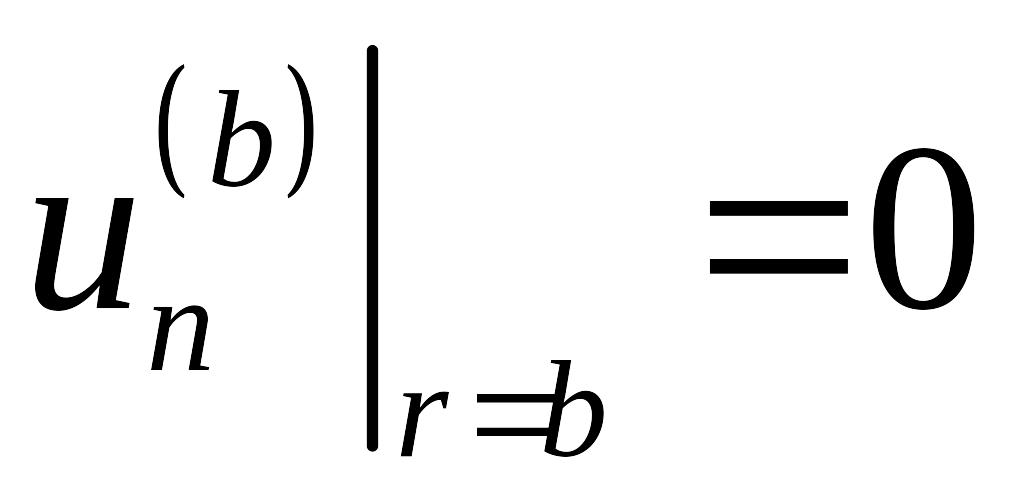.(5.23)
Заметим, что
, 
.
Теперь решение краевой задачи (5.18), (5.19) можно записать в виде разложения по этим частным решениям:
-
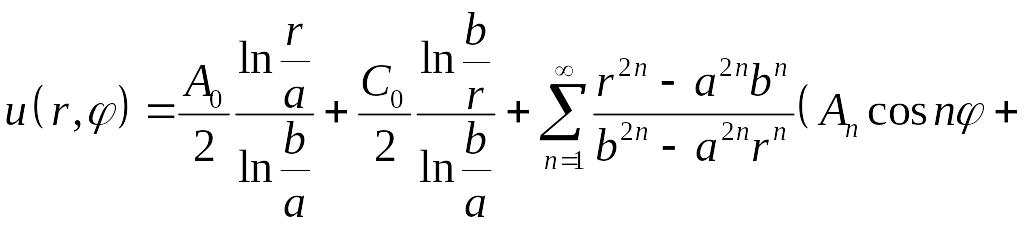
.(5.24)
Подставляя
(5.24) в граничное условие при
и учитывая (5.23), получаем
.
Отсюда
находим
и
:
-
,
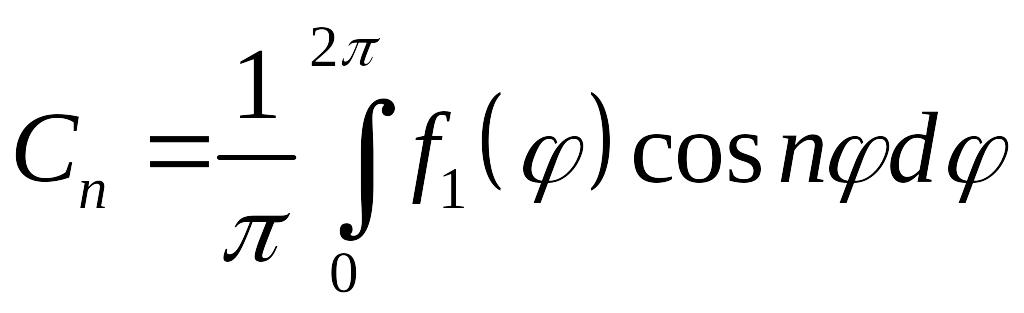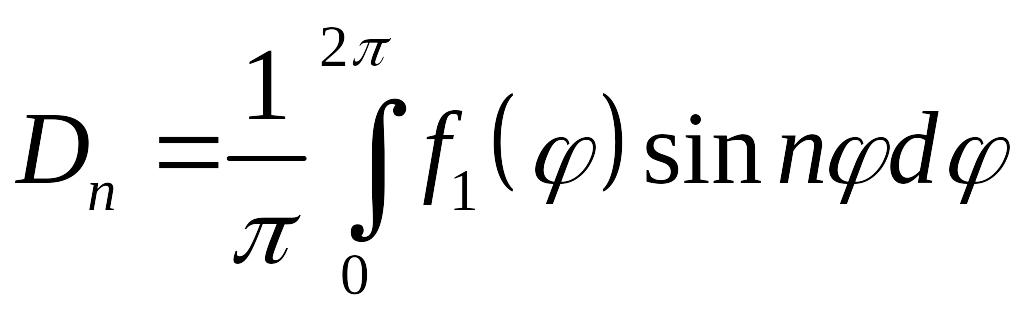.(5.25)
Аналогичным
образом, подставляя (5.24) в граничное
условие при
,
находим коэффициенты
и
:
-
,
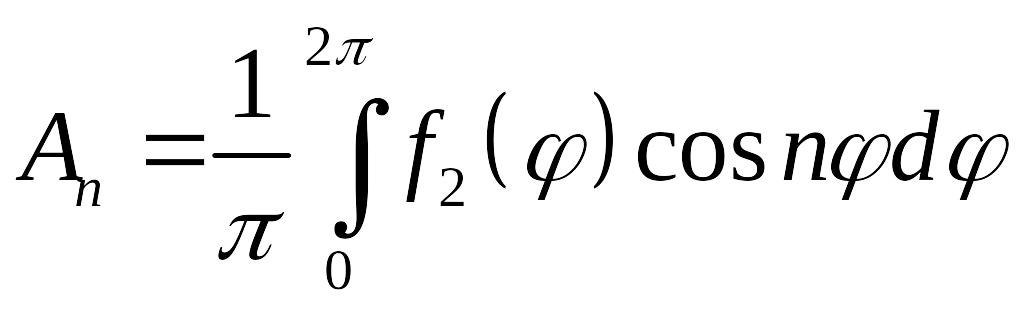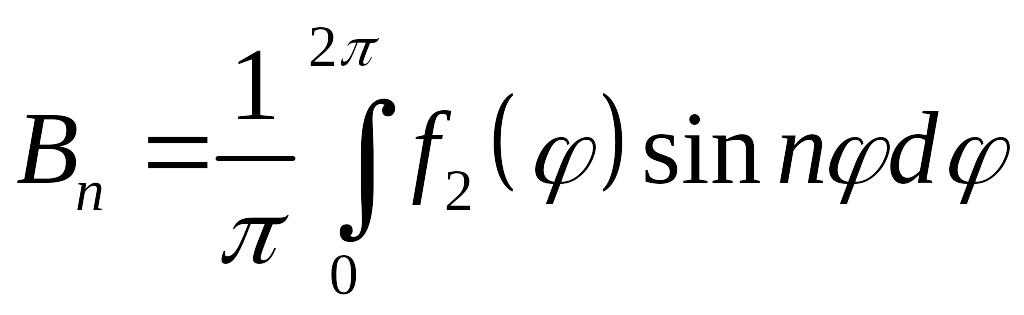.(5.26)
Таким
образом, построив предварительно
радиальные функции
и
,
удовлетворяющие нужным однородным
граничным условиям при
и
,
нам удалось «развязать» граничные
условия, заданные при
и при
.
Аналогичным образом можно поступать и при решении других краевых задач для уравнения Лапласа внутри кольца.
При
построении радиальных функций
для граничных условий второго рода
следует иметь в виду, что при
не существует двух линейно независимых
решений уравнения (5.21), одно из которых
удовлетворяет условию
,
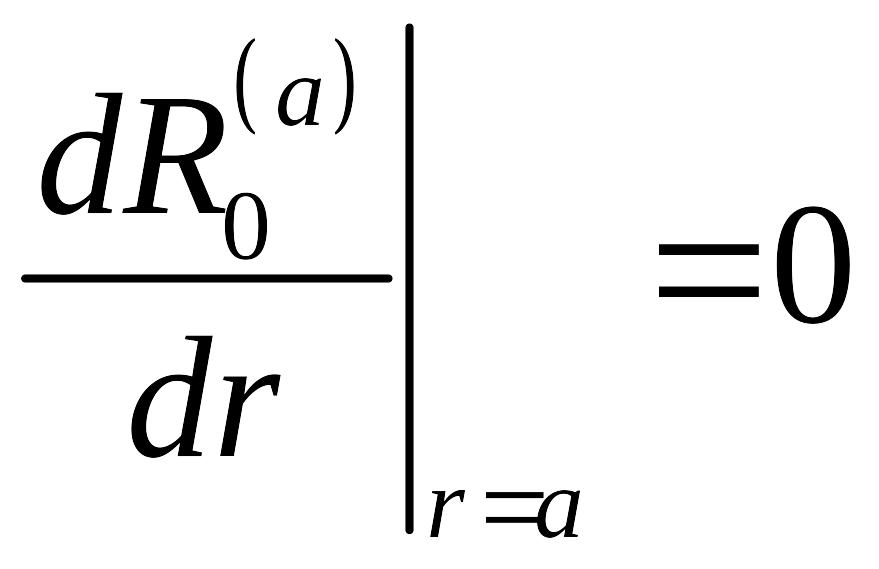а другое
.
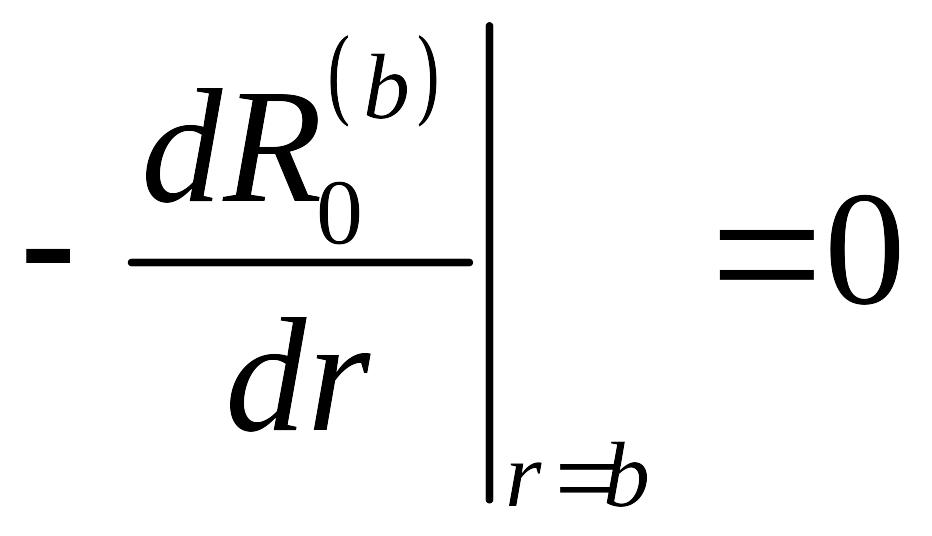Обоим этим условиям удовлетворяет одно
и то же решение
.
При
нужную пару фундаментальных решений
образуют функции
, 
, 
.
Поэтому решение задачи Неймана внутри кольца :
в кольце,
, 
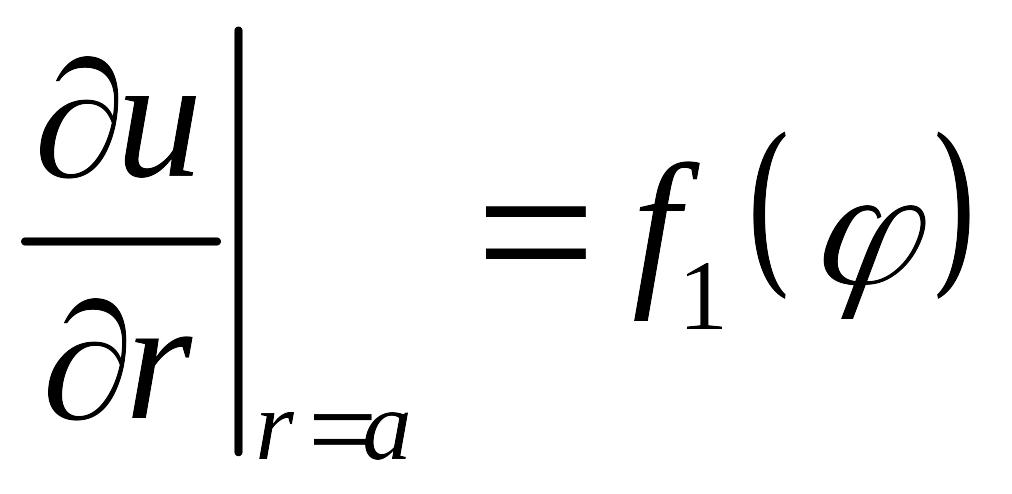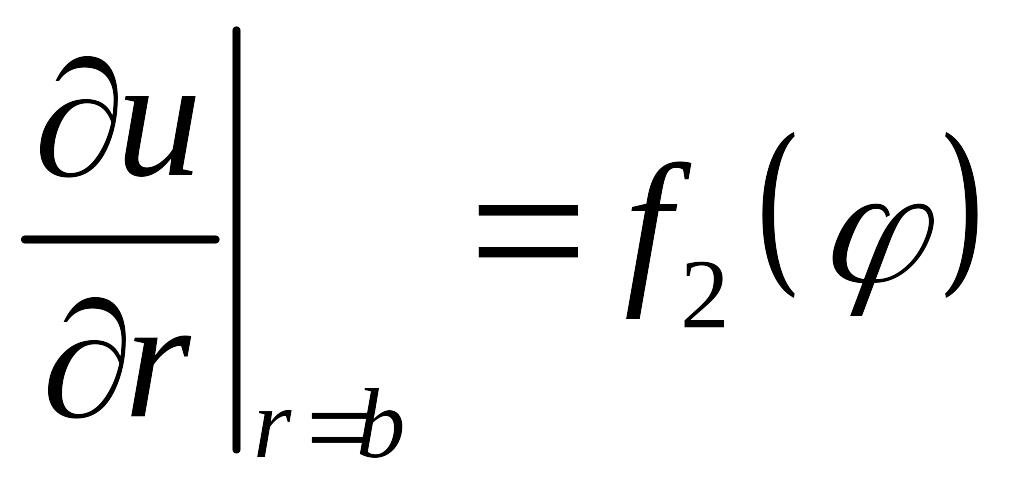
удобно записывать в виде ряда
-
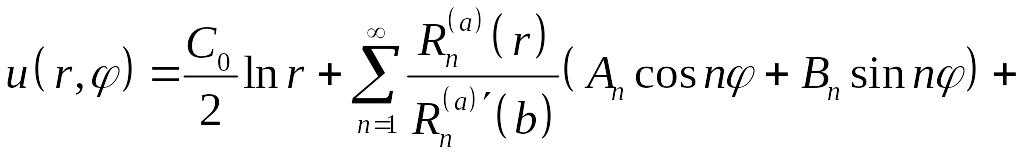
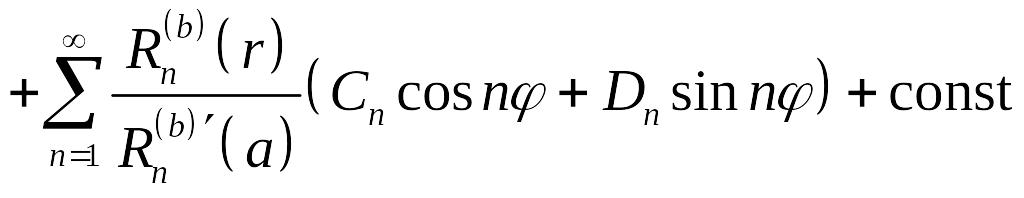,(5.27)
коэффициенты
которого определяются из граничных
условий по формулам (5.25), (5.26) при
,
коэффициент
равен
-
,
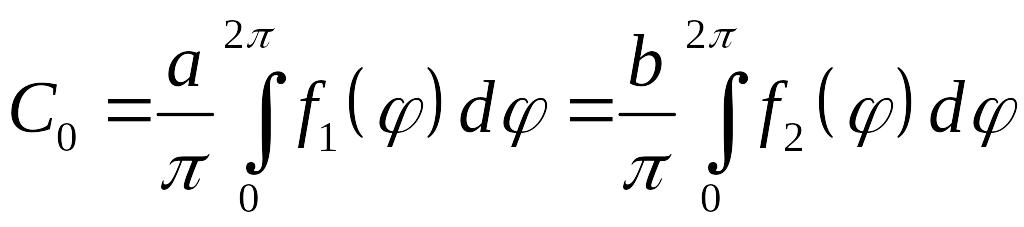(5.28)
а
– произвольная постоянная. Равенство
(5.28) противоречия при произвольных
функциях
и
не содержит, поскольку оно соответствует
условию разрешимости задачи Неймана
.
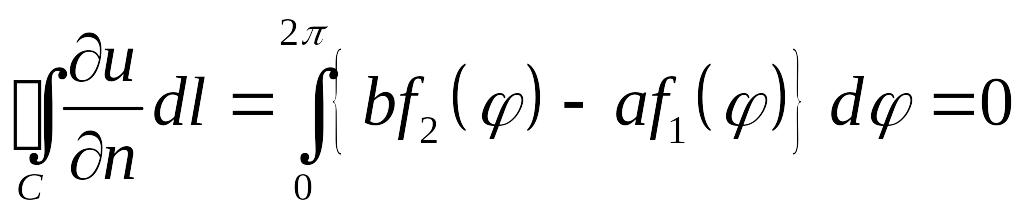Рассмотрим
вопрос о сходимости полученных рядов.
Рассмотрим, для примера, ряд (5.24). Поскольку
при
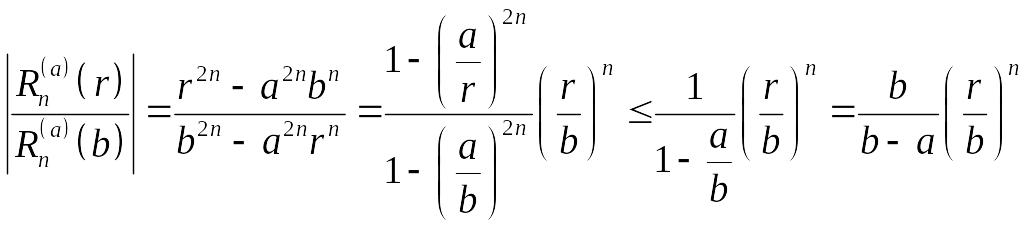
и
,
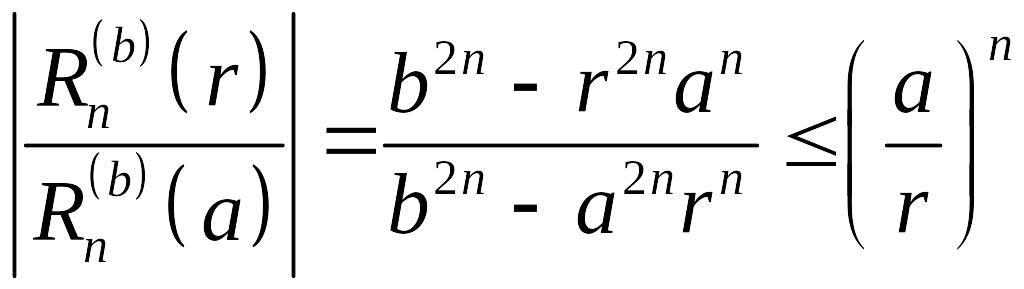ряды в (5.24) сходятся внутри кольца не хуже, чем геометрические прогрессии. При увеличении гладкости граничных функций и скорость сходимости увеличивается.
Рассмотрим примеры решения задач.
Внутри круга решить краевую задачу
, , ,
.
Решение. Общее решение задачи Дирихле внутри круга можно записать в виде
.
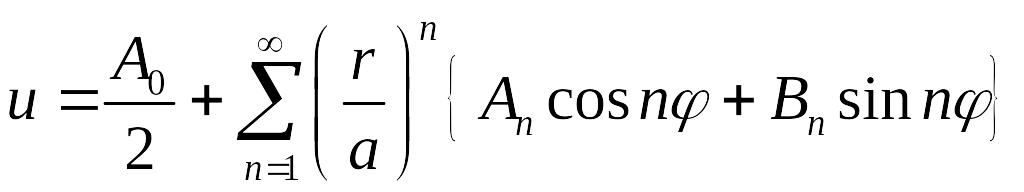Коэффициенты ряда определяются из граничного условия по формулам
,
.
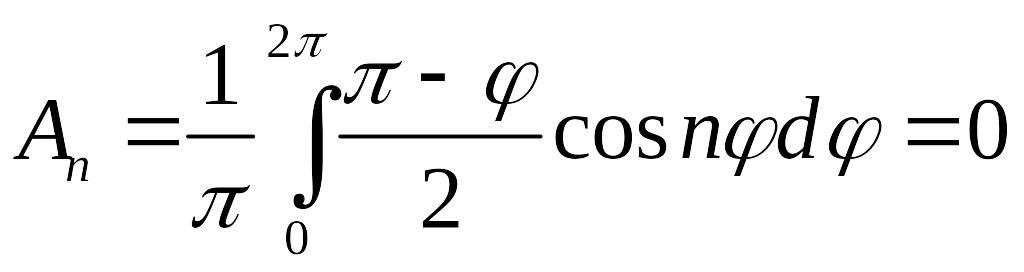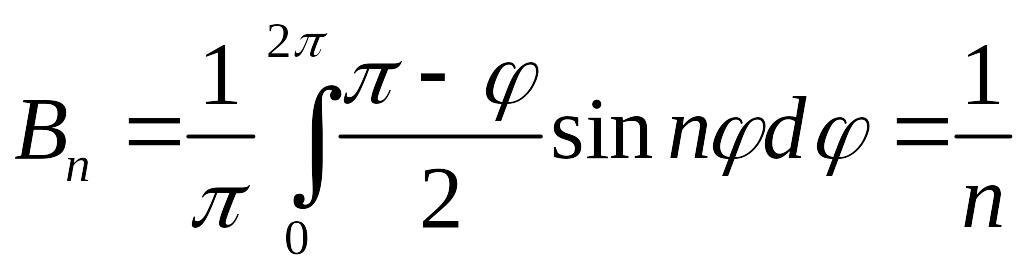Следовательно,
.
Внутри кольца решить краевую задачу
,
, 
.
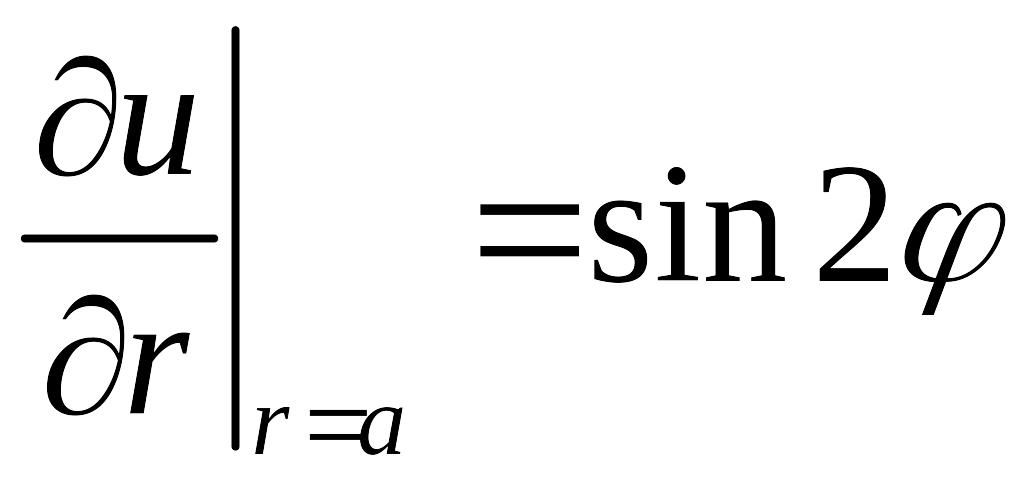Решение. Радиальные решения, удовлетворяющие однородному граничному условию при , имеют вид
,
,
,
а удовлетворяющие однородному граничному условию при –
, 
,
.
Поэтому решение поставленной задачи можно записать в виде
.
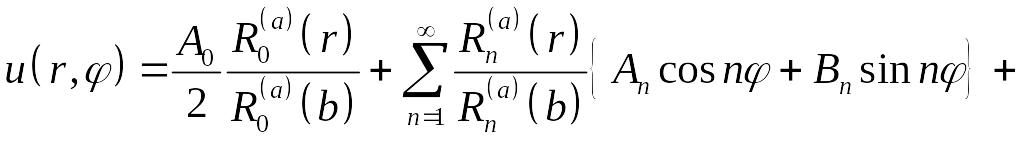
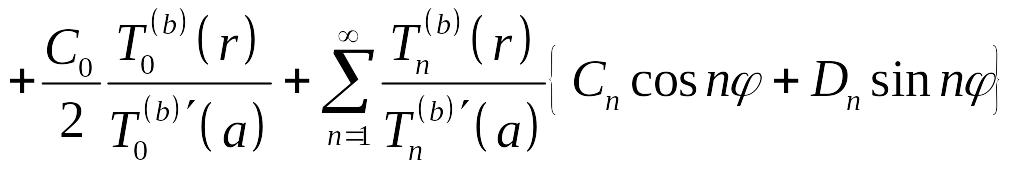Подставляя в граничное условие при , получим
.
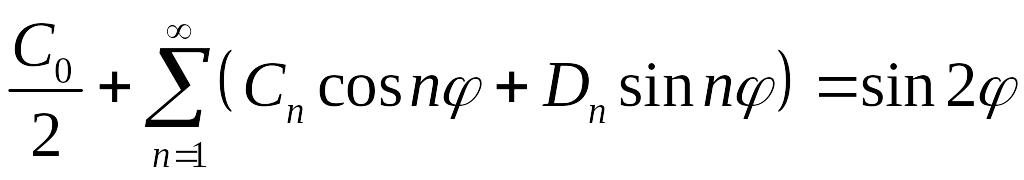Отсюда находим
,
, 
,
,
.
Подставляя общий вид уравнения в граничное условие при , получим
.
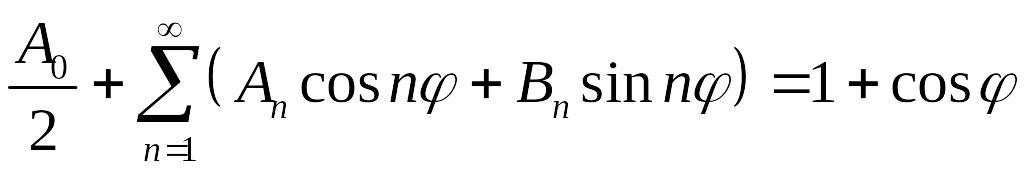Отсюда
,
,
,
, 
,
Следовательно,
.
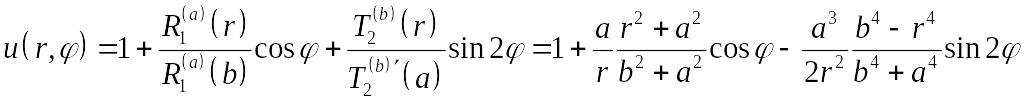Для задачи Дирихле внутри круга:
в круге ,
вывести формулу Пуассона
.
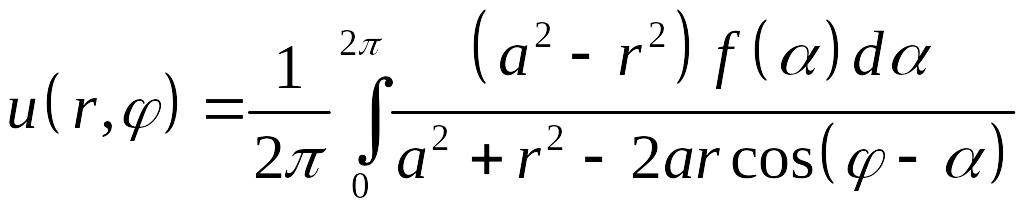Решение. Решение задачи Дирихле в круге может быть записано в виде ряда
-
,…,
(5.29)
коэффициенты которого определяются формулами
,
.
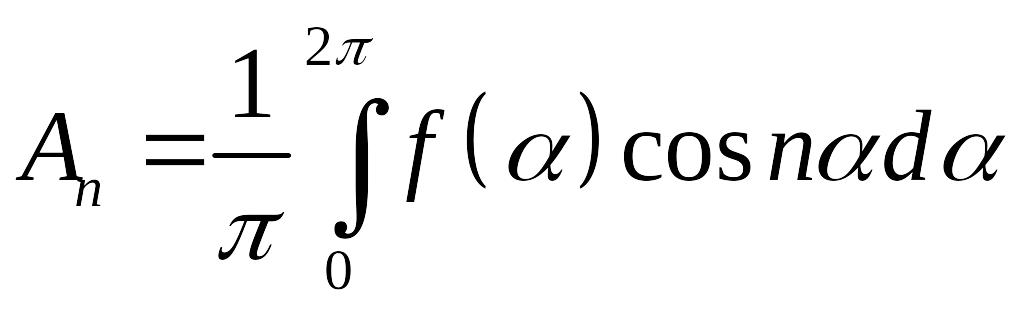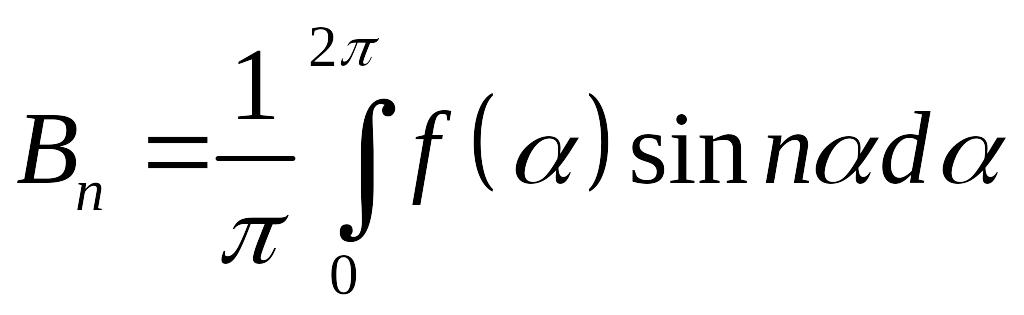Подставляя значения и в (5.29) и меняя порядок суммирования и интегрирования, получим
.
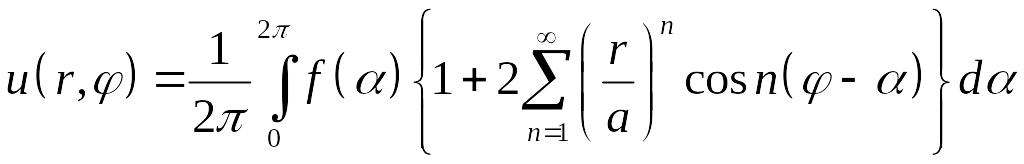Поскольку
при
,
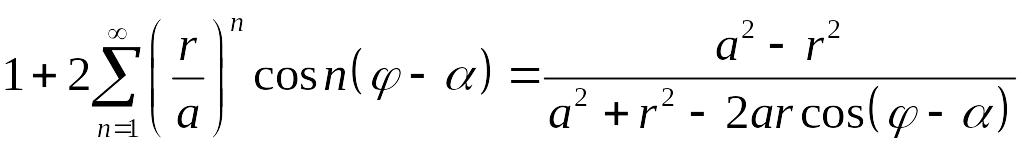можем записать
.
При непрерывной функции формула Пуассона даёт классическое решение задачи Дирихле в круге.