Ставропольский государственный университет Кафедра теоретической физики Практическое занятие 4.

Тема: УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. УРАВНЕНИЕ ЛАПЛАСА.

Смерек Ю.Л.

Ставрополь – 2009

Цель: Освоить основные методы решения внутренних и внешних краевых задач для уравнения Лапласа в системах с различной геометрической симметрией.

Формы работы:

• Выполнение коллективных и индивидуальных заданий.

Отчет:

• Ответы на контрольные вопросы.

• Защита результатов выполнения коллективных и индивидуальных заданий.

§ 1. Частные решения уравнения лапласа в полярной системе координат

Введем полярную систему координат и построим частные решения уравнения Лапласа

,

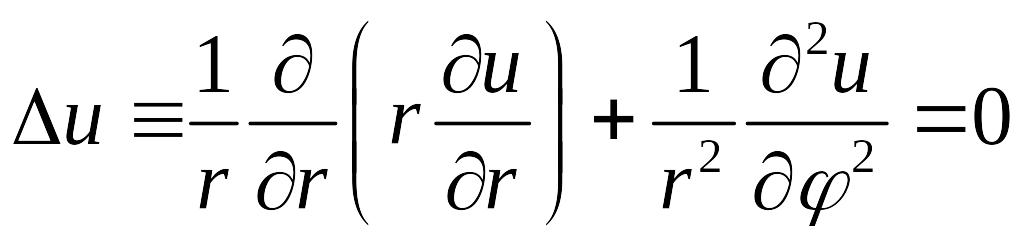представимые в виде

.

Для этого искомый вид решения подставляем в уравнение Лапласа и разделяем переменные:

.

(5.1)

Отсюда получаем отдельно уравнения для и . Рассмотрим сначала уравнение для :

/

Будем считать, что переменная изменяется от 0 до (случай, ко­гда переменная изменяется в меньшей области: , соответствует решению уравнения Лапласа в секторе). Если , то решение (в силу непрерывности) должно быть периодично по с периодом . Следовательно, для определения функции получаем одномерную задачу Штурма-Лиувилля с условиями периодичности

, ,

при любом ,

.

Эта задача имеет решение

.

Из (5.1) с учетом найденных значений получаем уравнение для :

.

Это уравнение Эйлера¹ и общее решение его может быть записано в виде

, ,

, .

Следовательно, построены следующие серии частных решений урав­нения Лапласа:

^a)

,

(5.2)

Эти решения ограничены при и неограничены на бесконечно­сти. Общее решение уравнения Лапласа в круге записыва­ется в виде разложения по этим решениям:

.

(5.3)

б)

,

(5.4)

Эти решения ограничены на бесконечности и неограничены при . Они используются при решении уравнения Лапласа вне круга. Об­щее решение уравнения Лапласа вне круга , ограниченное на бесконечности, может быть записано в виде

.

(5.5)

в) Треть серия решений

1, , , , ,

(5.6)

неограничена как при , так и при . Она используется при решении уравнения Лапласа в круговом кольце .

§ 2. Краевые задачи для уравнения лапласа внутри круга

Рассмотрим краевую задачу для уравнения Лапласа внутри круга :

в круге 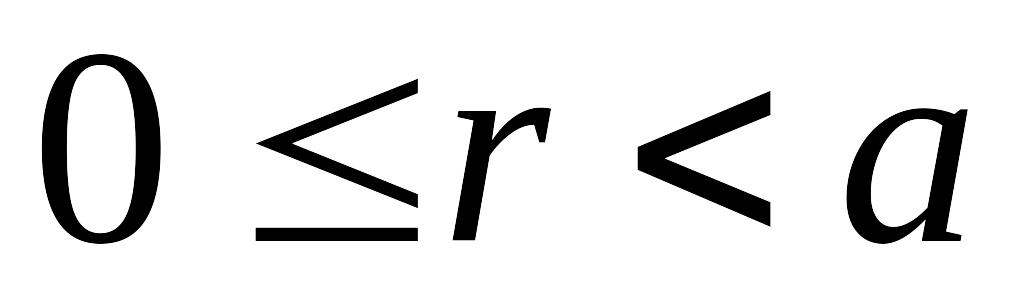,	(5.7)
, .	(5.8)

Решение этой краевой задачи можно записать в виде разложения (5.3), коэффициенты которого определяются из граничного условия (5.8). Но вычисления оказываются проще, если решение задачи (5.7), (5.8) записать в виде

(5.9)

. Подставляя (5.9) в граничное условие (5.8), получаем

.

Следовательно, и есть коэффициенты Фурье функции по системе тригонометрических функций , которые вычисляются по формулам

, ,

(5.10)

Выпишем отдельно решения первой, второй и третьей краевых задач для уравнения Лапласа в круге.

1. Задача Дирихле: ,

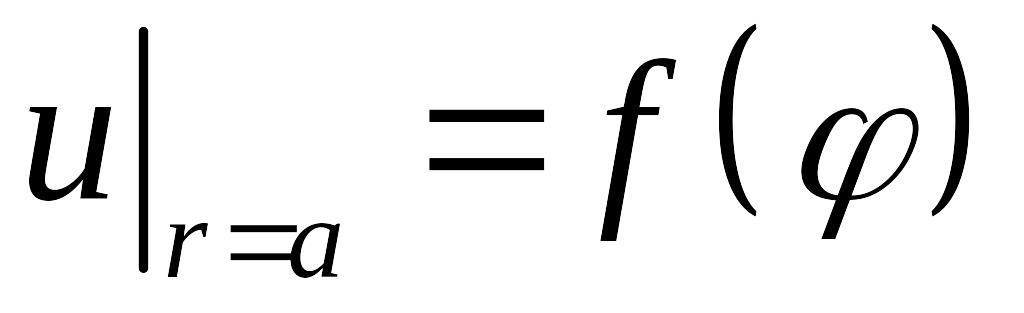   (5.11)

2. Задача Неймана: ,

,

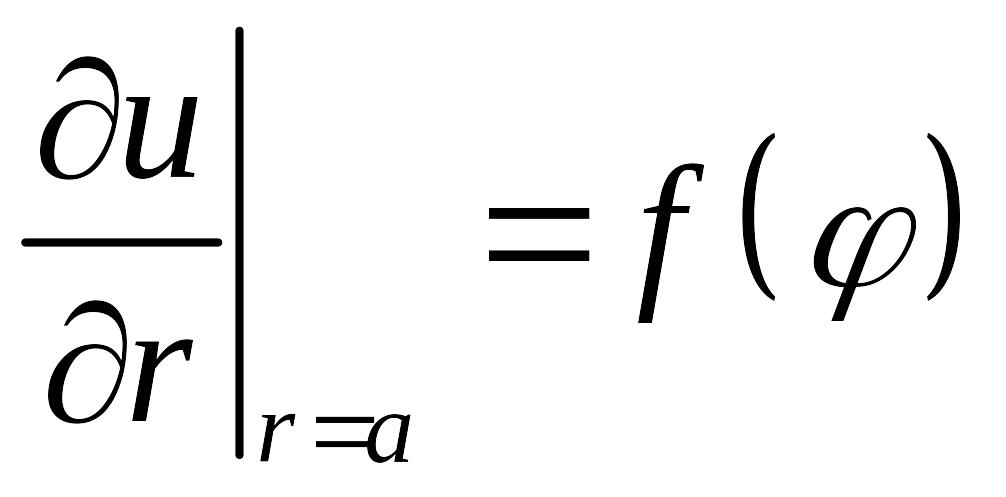(5.12)

где – произвольная постоянная. Напомним, что решение внутренней задачи Неймана существует только при условии

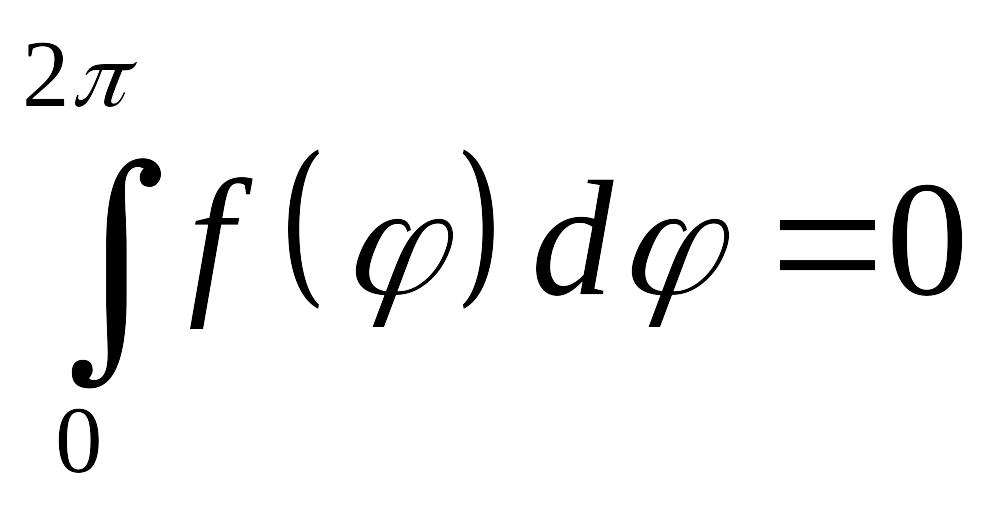
(это условие необходимое и достаточное) и определяется с точностью до произвольной постоянной.

3. Третья краевая задача: , ,

.

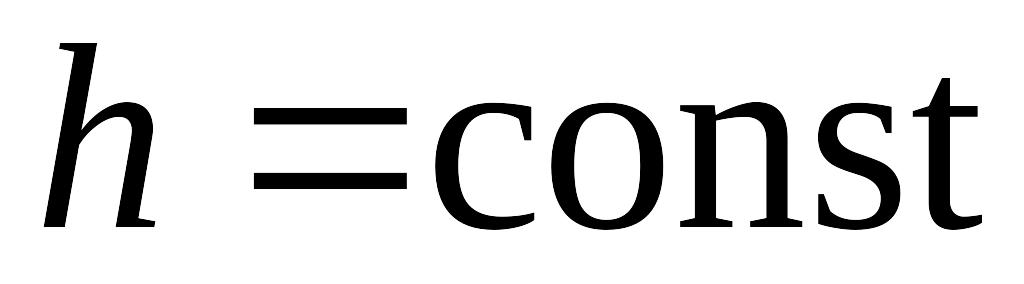(5.13)

Коэффициенты в разложениях (5.11) – (5.13) определяются по формулам (5.10).

Остановимся кратко на вопросе о сходимости рядов (5.11) – (5.13). Если граничная функция абсолютно интегрируема, то ее ко­эффициенты Фурье, по крайней мере, ограничены, и, как видно из структуры указанных рядов, эти ряды будут в любой внутренней точке круга сходиться не хуже, чем геометрическая прогрес­сия со знаменателем . При увеличении гладкости функции сходимость указанных рядов улучшается.