Индивидуальные задания для самостоятельной работы

1-й вариант

Задача 1. Найти функцию , определяющую процесс колебания струны , закрепленной на концах и возбуждаемой (рис. 2) оттягиванием ее в точке на величину , т.е. . Начальная скорость равна нулю.

З адача 2. Найти установившиеся колебания неоднородного стержня, составленного из двух однородных стержней, соединенных в точке , если один конец стержня закреплен, а второй движется по закону

.

2-й вариант

Задача 1. Закрепленная на концах струна в точке оттянута силой . Найти колебания струны, если в начальный момент сила перестает действо­вать, а начальная скорость равна нулю.

Задача 2. Найти установившиеся колебания пружины, один конец которой закреплен, а на второй действует сила

.

3-й вариант

Задача 1. Найти функцию , определяющую процесс колебания струны , закрепленной на концах и возбуждаемой импульсом , распределен­ным на отрезке : а) равномерно, б) по закону , если начальное отклонение равно нулю.

Задача 2. Решить задачу о колебаниях неоднородного стержня длины с жестко закрепленными концами, составленного из двух однородных стерж­ней, соединенных в точке ( ), если начальное отклонение имеет вид

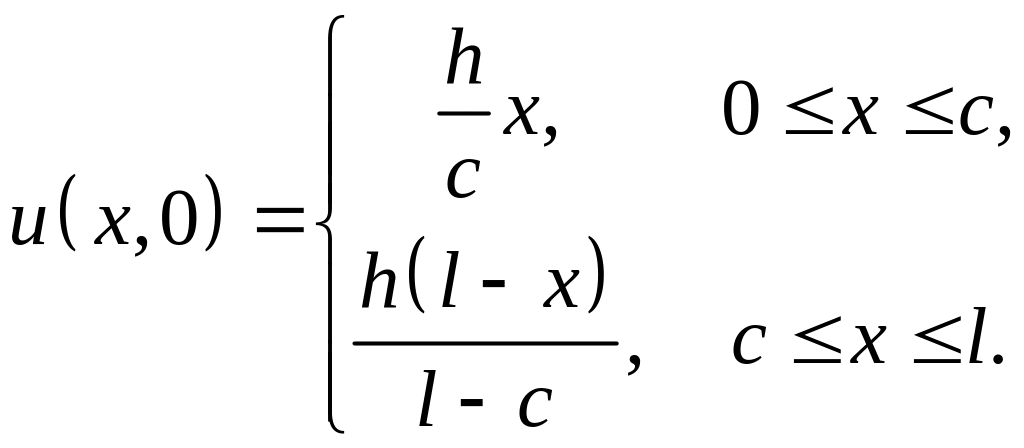
а начальные скорости равны нулю.

4-й вариант

Задача 1. Найти функцию , определяющую процесс колебания струны , закрепленной на концах и возбуждаемой импульсом , приложенным в точке . Начальное отклонение равно нулю.

Задача 2. К однородной струне с закрепленными концами и в точке ( ) приложена гармоническая сила

,

действующая начиная с момента . Найти отклонение струны , предполагая начальные условия нулевыми.

5-й вариант

Задача 1. Пружина, закрепленная одним концом в точке , растянута гру­зом массы , подвешенным в точке . Найти колебания пружины, если в момент груз падает и в дальнейшем на конец не действуют никакие силы.

Задача 2. Упругий стержень длины расположен вертикально и жестко при­креплен верхним концом к свободно падающему лифту, который, достигнув скорости , мгновенно останавливается. Найти колебания стержня, пред­полагая его нижний конец свободным.

6-й вариант

Задача 1. Один конец стержня закреплен, а на второй действует сила . Най­ти колебания стержня, если в начальный момент сила перестает действо­вать.

Задача 2. Струна с закрепленными концами колеблется под действием гармо­нической силы, распределенной с плотностью . в среде, сопротивление в которой пропорционально скорости. Найти отклонение струны при произвольных начальных условиях и установившиеся колебания, составляющие главную часть решения при .

7-й вариант

Задача 1. Исследовать процесс колебания пружины, один конец которой закреп­лен, а ко второму концу в начальный момент подвешивается груз массы . Начальные условия нулевые.

Задача 2. Изолированный электрический провод длины с характеристика­ми , , заряжен до некоторого потенциала . В начальный момент один конец провода заземляется, а второй остается все время изоли­рованным. Найти распределение напряжения в проводе.

Задача 3. Используя систему Mathematica, постройте профиль струны для различных моментов времени:

, ,

в сле­дующих случаях, соответствующих Вашему варианту:

1 ) начальная скорость неограниченной струны ( ) равна нулю ( ), а начальный профиль струны задан в виде рис. 3;

2) начальное отклонение неограниченной струны ( )равно нулю, а начальная скорость имеет по­стоянное значение на участке струны и равна нулю вне этого участка;

3) начальные условия для неограниченной струны ( ) имеют вид

,

4) начальная скорость полуограниченной струны ( ) равна нулю ( ), а начальное отклоне­ние задано в виде треугольника, изображенного на рис. 21. Конец струны закреплен;

5) начальная скорость полуограниченной струны ( ) равна нулю ( ), а начальное отклоне­ние задано в виде треугольника, изображенного на рис. 21. Конец струны свободен;

6) начальные условия полуограниченной струны ( ) имеют вид

,

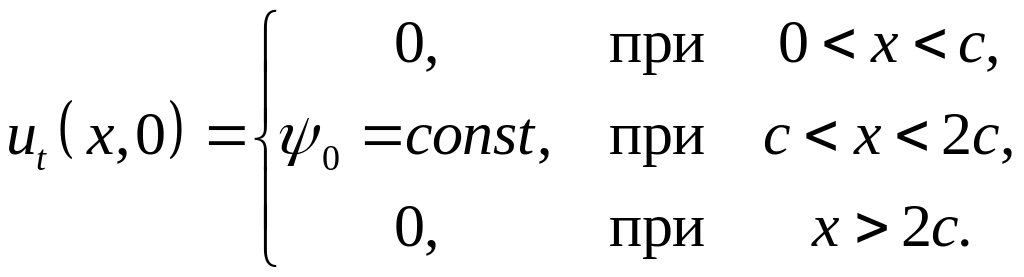
конец струны закреплен;

7) начальные условия полуограниченной струны ( ) имеют вид

,

конец струны свободен.