2. Исследование физических процессов, приводящих к уравнениям гиперболического типа

25. В начале длинной цилиндрической трубки, заполненной газом, на­ходится поршень, движущийся по произвольному закону со скоро­стью . Начальное смещение и скорость частиц газа равны ну­лю. Найти смещение газа в сечении с абсциссой . Рассмотреть случай движения поршня с постоянной ско­ростью .

26. Неограниченный упругий стержень получен соединением в точке двух стержней с характеристиками

, , при ,

, , при .

а) Пусть из области бежит волна

,

где – заданная функция. Найти коэффициенты отражения и преломления волны при прохождении через точку стыка . Установить, при каких условиях отраженная волна отсутствует.

б) Решить аналогичную задачу, если задано локальное начальное от­клонение

а начальная скорость равна нулю.

27. Полуограниченная трубка ( ), заполненная идеальным газом, имеет на одном конце , свободно перемещающийся поршень массы . В момент времени поршню при помощи удара сообщают началь­ную скорость 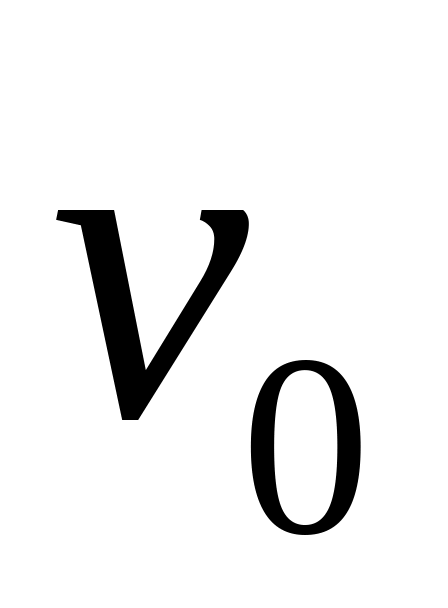. Исследовать процесс распространения волны в газе, если известно, что начальные отклонения и начальная скорость частиц газа рав­ны нулю.

Указание. Рассмотреть решение уравнения колебаний в области . Использовать начальные условия на границе , и граничное условие

.

Здесь – начальное давление газа, – площадь поперечного сечения трубки, .

28. Б есконечная струна, имеющая в точке сосредоточенную массу , находится в положении равновесия. В начальный момент времени ударом молоточка массе сообщается начальная скорость . Доказать, что в момент времени возмущенная струна имеет вид, указанный на рис. 1, где и 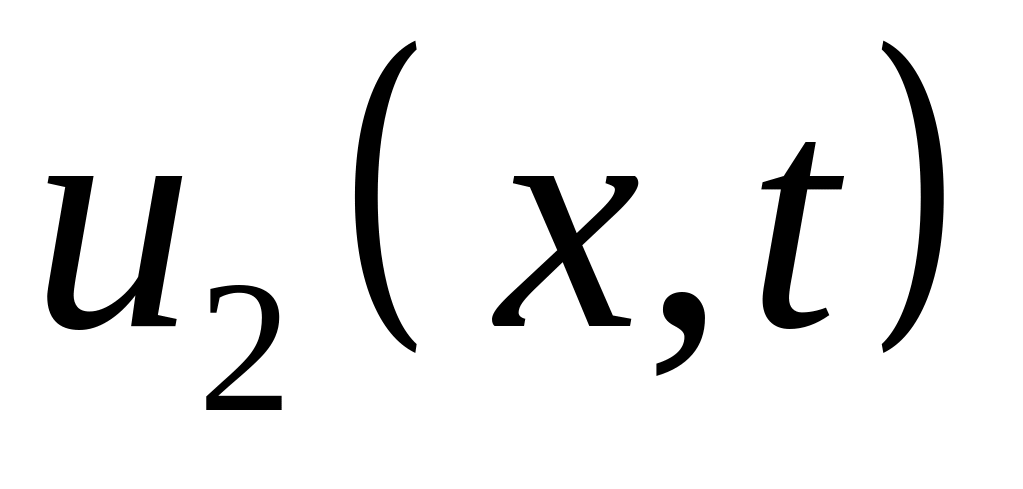определяются формулами

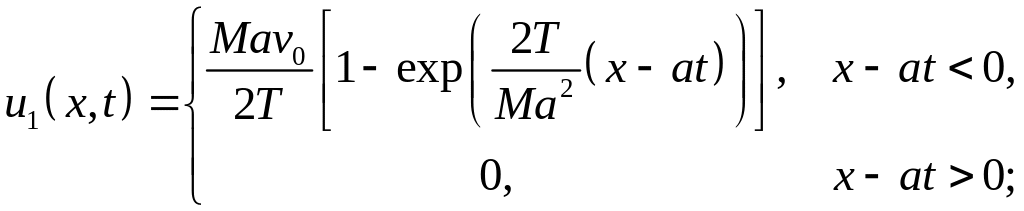
Указание. Воспользоваться условием

.

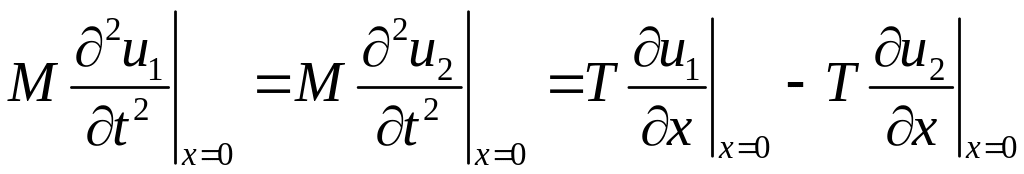29. К однородной струне с закрепленными концами и в точке 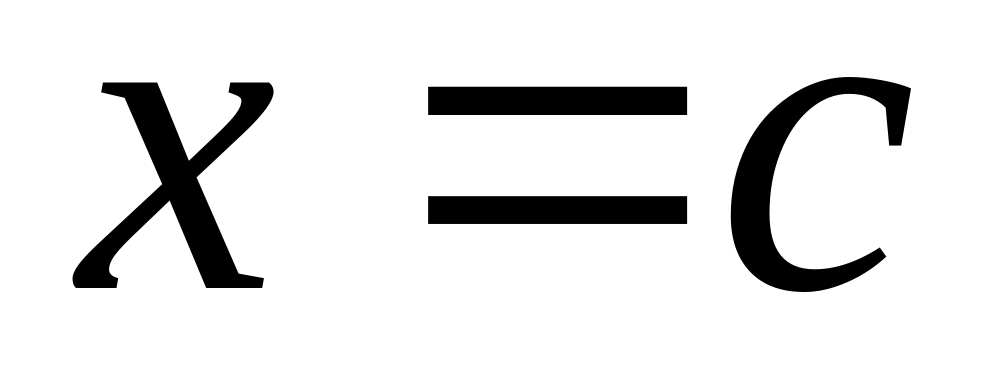прикреплена масса . Найти отклонение струны , если: а) в начальный момент в точке струна оттянута на величину от положения равновесия и отпущена без начальной скорости; б) начальное отклонение и начальная скорость равны нулю.

30. Исследовать процесс колебания пружины со свободными концами при равномерном начальном растяжении (представить модель этой задачи).

31. Исследовать процесс колебания пружины с упруго закрепленными концами при одинаковых коэффициентах жесткости, если начальные усло­вия произвольны.

Решение исследовать при малых («мягкое» закрепление) и при боль­ших («жесткое» закрепление) и вычислить соответствующие поправки к собственным значениям для струны со свободными и закрепленными конца­ми.

32. Найти отклонение струны с жестко закрепленными конца­ми, если колебания происходят в среде, сопротивление которой пропорцио­нально скорости, а начальные условия произвольны.

33. Струна с закрепленными концами колеблется под действием гармо­нической силы, распределенной с плотностью . Найти отклонение струны при произвольных начальных условиях. Иссле­довать возможность резонанса и найти решение в случае резонанса.

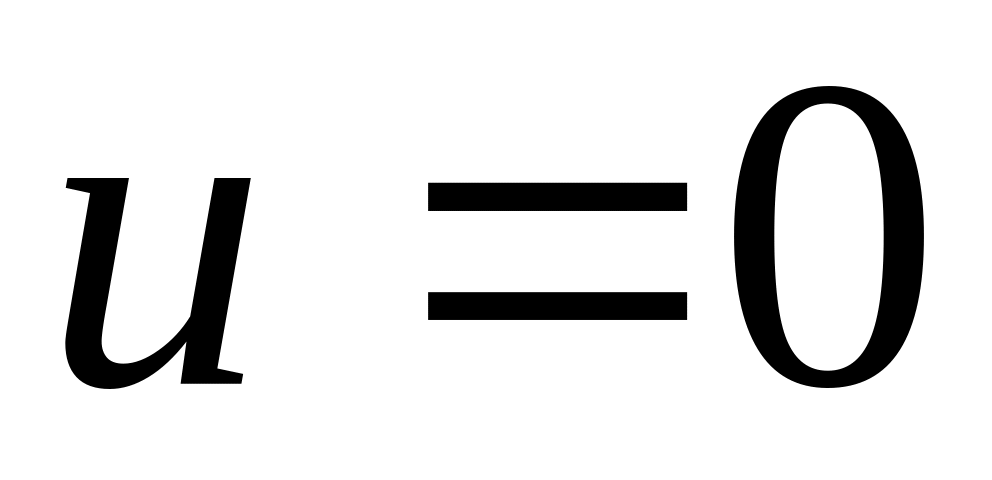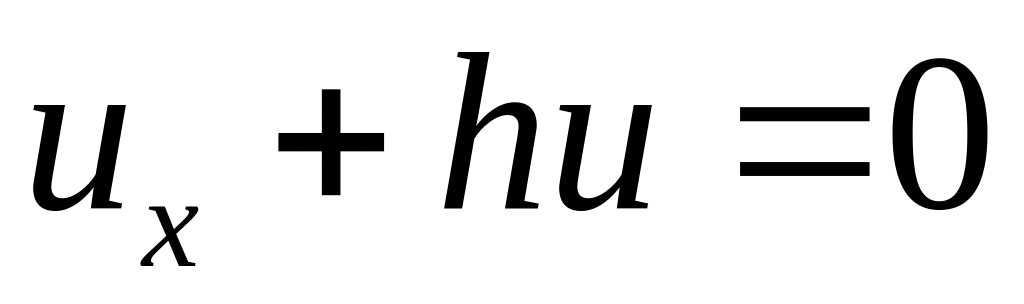34. Доказать аддитивность энергии отдельных гармоник для процесса колебаний при граничных условиях , . Рассмотреть также случай граничного условия 3-го рода (все ряды предполагать равномерно сходящимися).