Задания для самостоятельной работы
Решение краевых задач для уравнения колебаний методом разделения переменных
Решить начально-краевую задачу для уравнения колебаний на отрезке:
,
,
;
,
,
;
,
,
.
Решить начально-краевую задачу на отрезке:
,
,
;
,
;
,
,
.
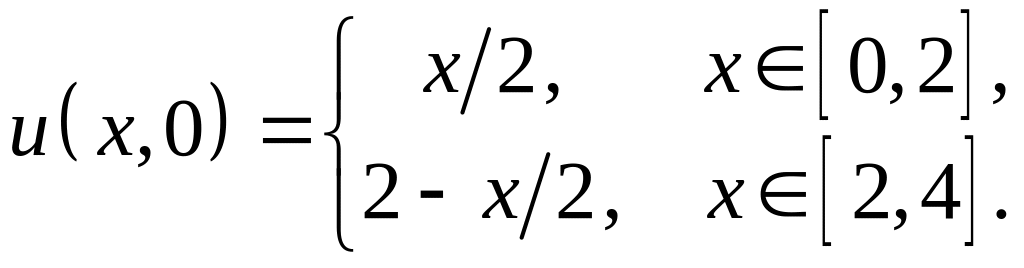
Решить начально-краевую задачу на отрезке:
,
,
;
,
, 
;
, 
,
.
Решить начально-краевую задачу на единичном отрезке:
,
,
;
,
,
;
,
,
.
Решить начально-краевую задачу на отрезке:
, , ;
,
,
;
,
,
.
Решить начально-краевую задачу на отрезке:
,
,
;
, , ;
,
,
.
Решить начально-краевую задачу на единичном отрезке:
, , ;
,
,
;
,
,
.
Решить уравнение
при нулевых начальных условиях и граничных условиях
,
,
где
,
и
– постоянные.
Решить дифференциальное уравнение
при нулевых начальных условиях и граничных условиях
,
,
где
,
и
– постоянные.
Решить начально-краевую задачу в прямоугольнике:
,
,
,
;
,
,
,
;
,
;
,
,
.
Решить начально-краевую задачу в круге:
,
,
,
;
,
,
,
;
,
,
.
Здесь
– пятый корень уравнения
.
Решить начально-краевую задачу в шаре
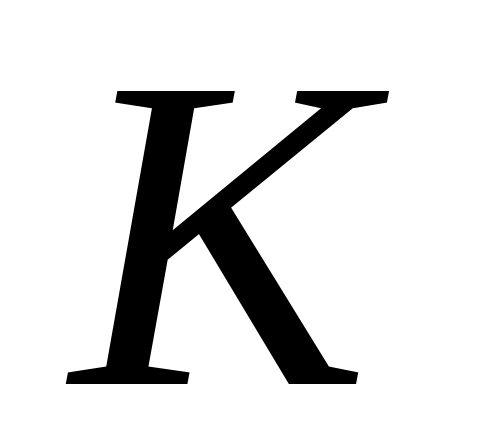радиуса
:
,
,
;
,
,
;
,
.
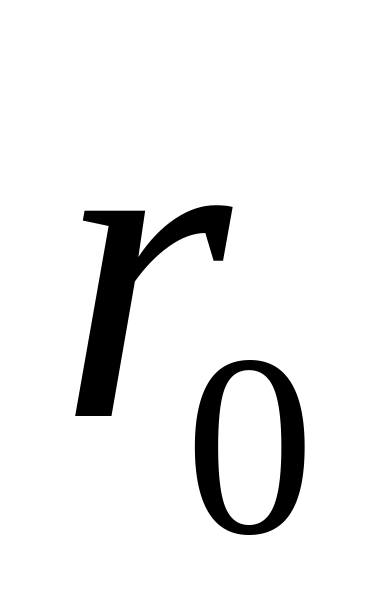Область
представляет собой объединение области
и ее границы.
Решить начально-краевую задачу в шаровом слое:
,
,
,
,
;
,
,
,
;
,
,
.
Решение задачи Коши для уравнения колебаний методом характеристик
Начальная задача (задача
Коши) для уравнения колебаний на
бесконечной прямой
с постоянными коэффициентами заключается
в определении в области
функции
,
удовлетворяющей уравнению колебаний
и двум начальным условиям:
-
, 
,
, 
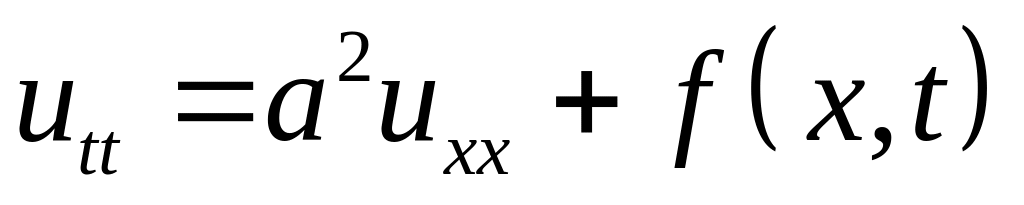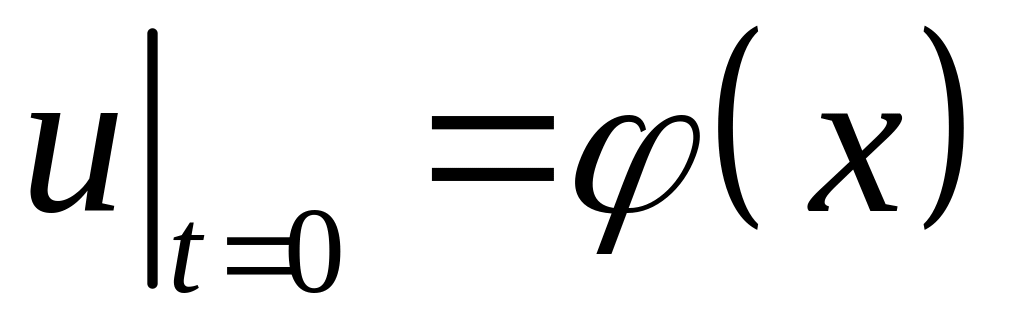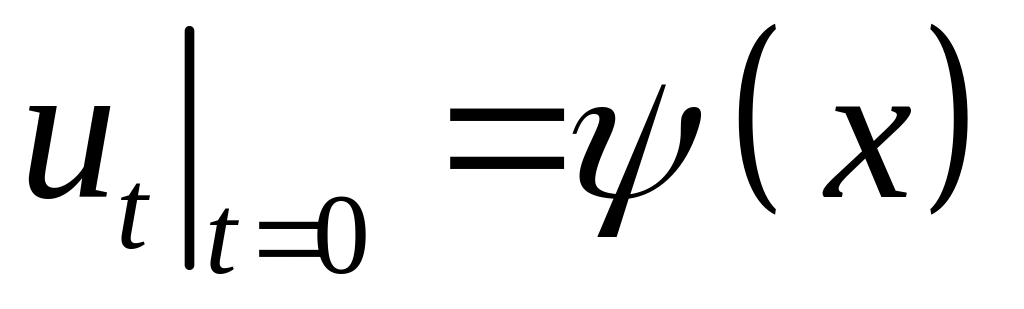.(6.10)
Классическим решением задачи с начальными
условиями называется функция
,
непрерывная вместе со своими первыми
производными по
в замкнутой области
,
имеющая непрерывные производные второго
порядка в открытой области
,
удовлетворяющая в
уравнению колебаний и при
начальным условиям.
Если функция
дважды непрерывно дифференцируема,
функция
непрерывно дифференцируема на бесконечной
прямой
,
а функция
непрерывно дифференцируема в области
,
то классическое решение задачи (6.10)
может иметь обобщённое решение.
Учитывая линейность задачи (6.10), можно провести её редукцию и представить решение в виде суммы решений двух задач:
,
где
– решение начальной задачи для однородного
уравнения колебаний с неоднородными
начальными условиями,
– решение начальной задачи для
неоднородного уравнения колебаний с
однородными начальными условиями.
Для решения начальной задачи для уравнения колебаний на бесконечной прямой эффективно использовать метод интегрального преобразования Фурье. Здесь приведены примеры решения задач для уравнения колебаний на бесконечной прямой методом интегрального преобразования Фурье.
Рассмотрим начальную задачу для однородного уравнения колебаний на бесконечной прямой:
-
,
,, .
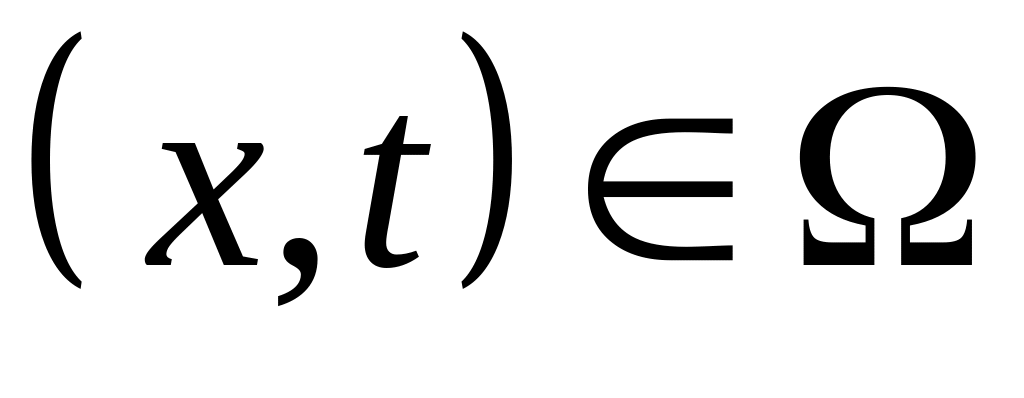(6.11)
Применим преобразование Фурье с ядром
и обозначим через
,
и
образы Фурье функций
,
и
соответственно:
,
,
.
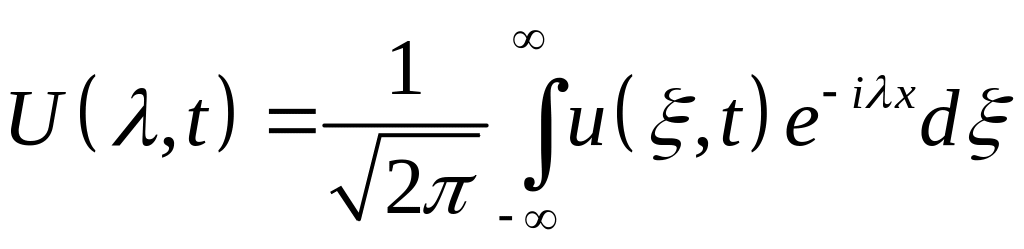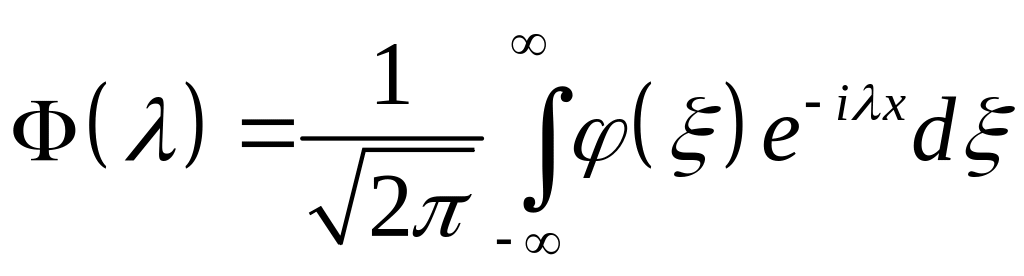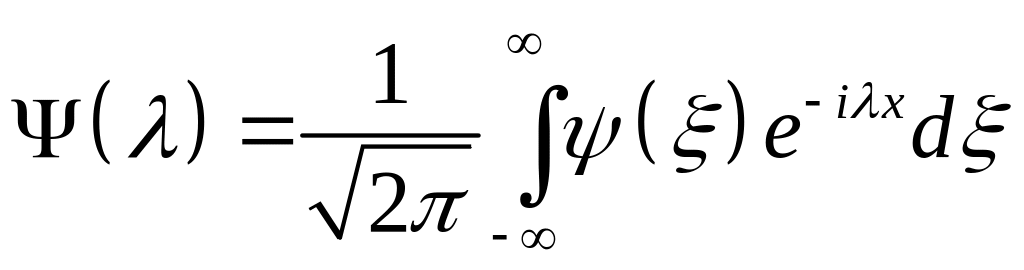Предположим, что выполнены условия
существования интеграла Фурье (это
заведомо выполнено для классического
решения задачи) и что функция
и её частные производные достаточно
быстро стремятся к нулю при
.
Предположим также, что интеграл для
можно дифференцировать по переменной
под знаком интеграла.
Умножая уравнение колебаний и начальные
условия на
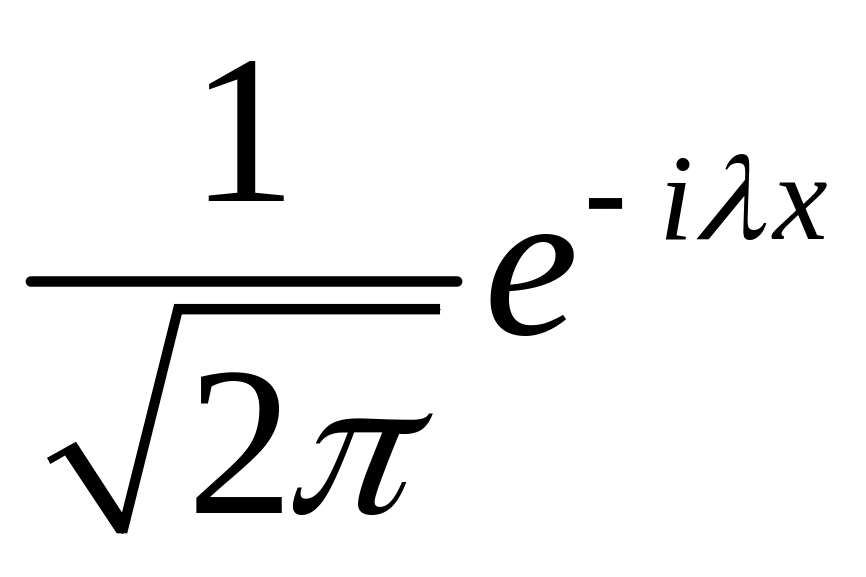и интегрируя по
от
до
,
получим для функции
,
зависящей от параметра
,
задачу Коши:
,
,
, 
,
решение которой имеет вид
.
Воспользовавшись формулой обратного преобразования Фурье, возвратимся от изображения к оригиналу :
,
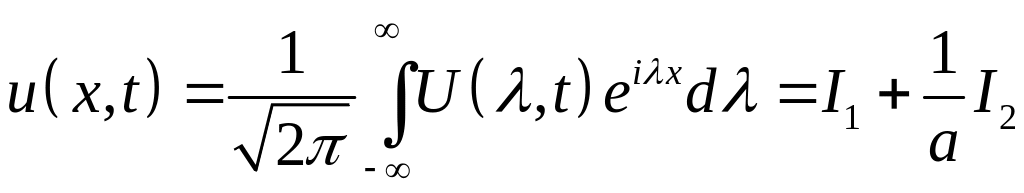где
,
.
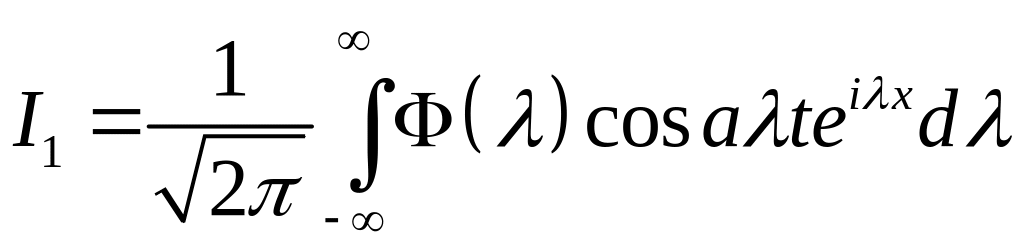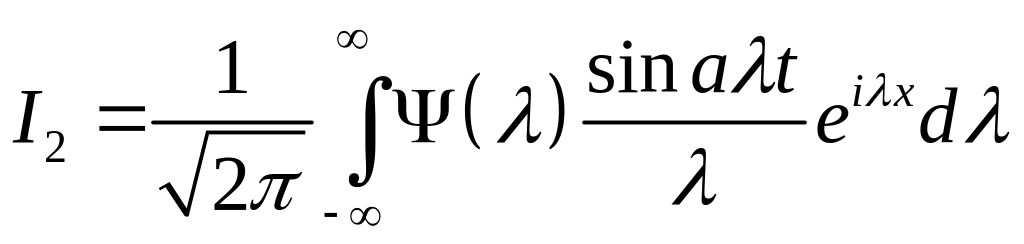Рассмотрим интеграл
.
Используя выражение для
,
получим
.
Используя формулу
и известное интегральное представление дельта-функции3
.
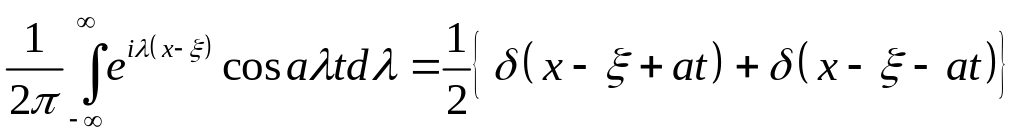С помощью последней формулы получим
.
Перейдём к интегралу
.
Подставляя в него выражение для
,
будем иметь
.
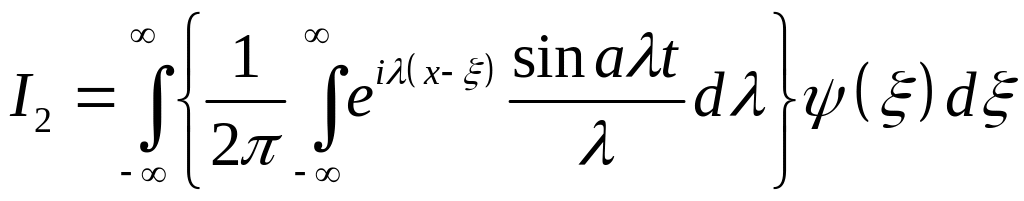Для вычисления внутреннего интеграла воспользуемся формулой
-
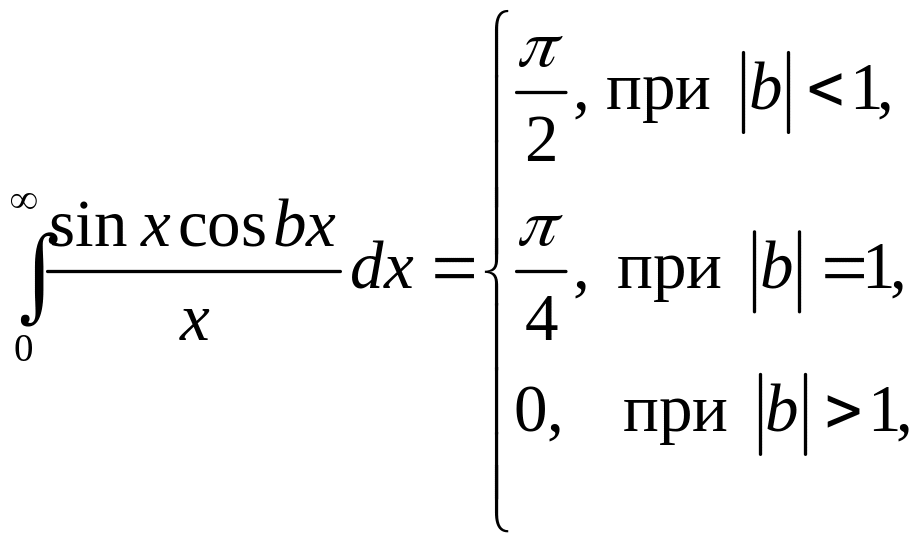
(6.12)
которую несложно получить, вычисляя интеграл в левой части с помощью вычетов4.
Вводя замену
,
получим
-
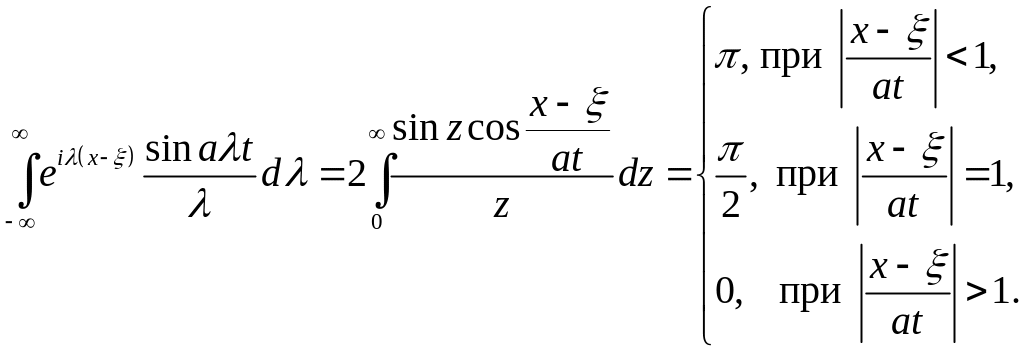
(6.13)
Таким образом,
.
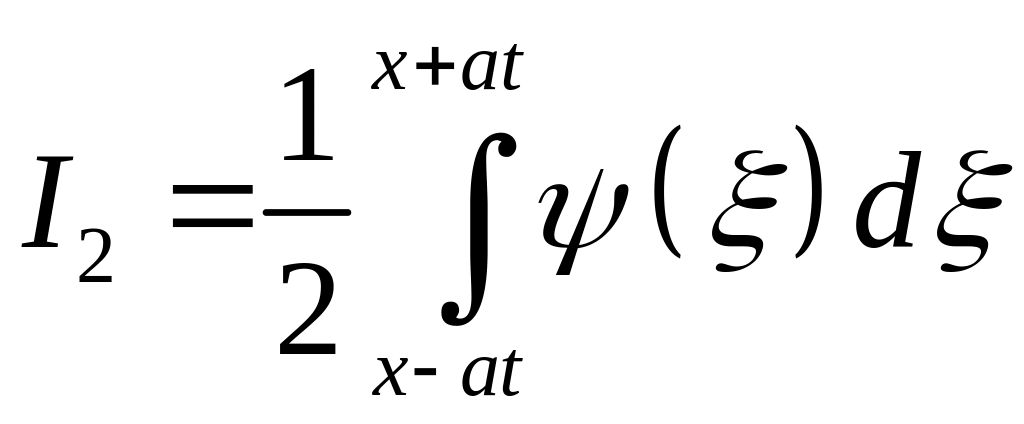Используя выражения для интегралов и , получаем окончательный ответ:
-
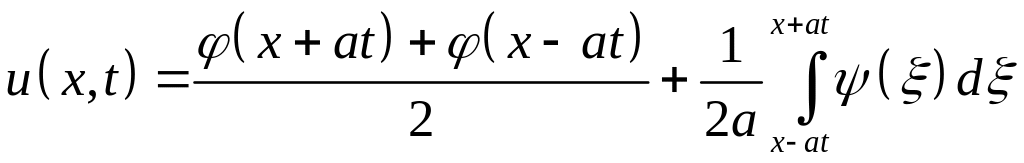
(6.14)
Полученное выражение (6.14) для решения задачи (6.10) носит название формулы Даламбера.
Формула Даламбера (6.14) получена нами с помощью метода интегрального преобразования Фурье. Из неё следуют единственность, устойчивость и существование решения задачи (6.10)5.
При этом решение представляется в виде суперпозиции двух бегущих волн:
-
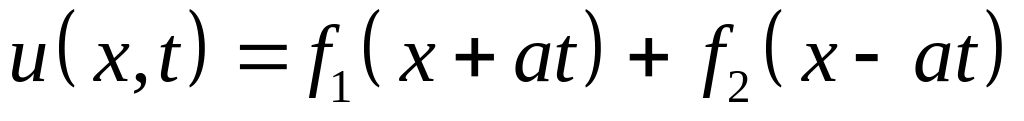,(6.15)
где
– правая бегущая волна:
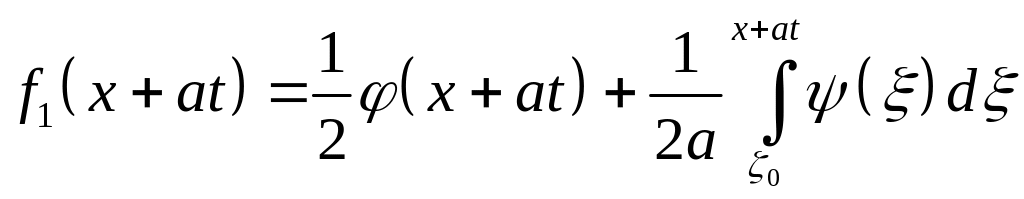
и
– левая бегущая волна:
.
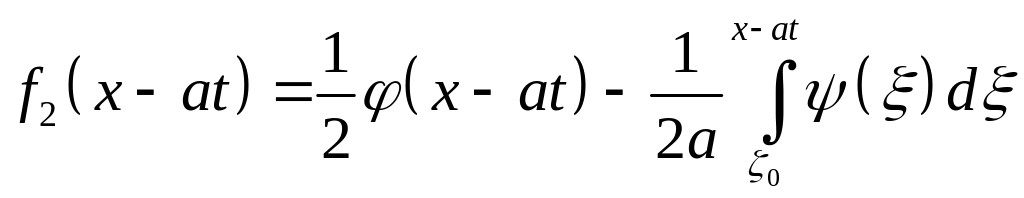Можно было сразу искать решение задачи (6.10) в виде (6.15). Такой подход к решению задачи носит название метода распространяющихся волн, или метода Даламбера. Рассмотрим его подробней. Предположим, что существует классическое решение задачи (6.10). Преобразуем однородное уравнение колебаний к каноническому виду, содержащему смешанную производную. Характеристическое уравнение для однородного уравнения колебаний имеет вид
и распадается на два уравнения:
, 
.
Характеристиками являются два семейства прямых:
, 
.
Сделаем замену переменных
, 
.
В переменных
и
однородное уравнение колебаний принимает
вид
-
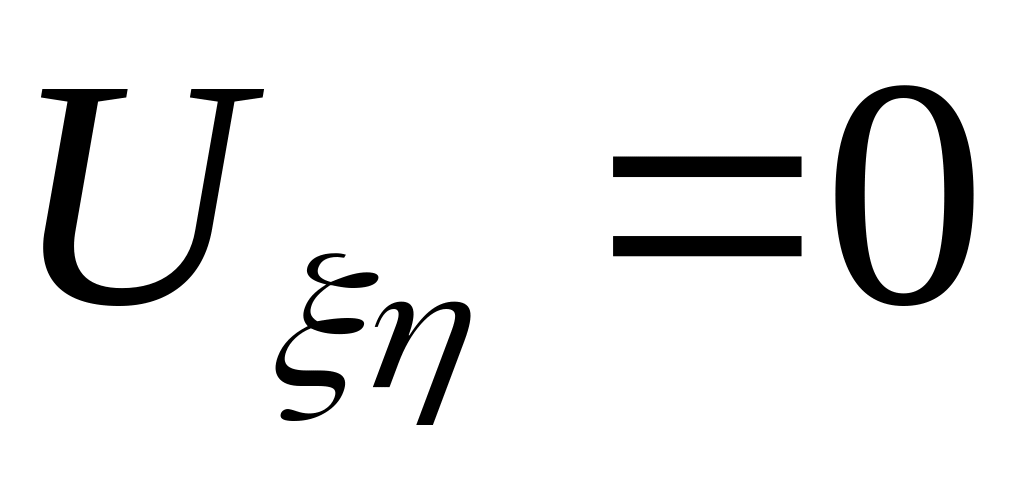,(6.16)
где
.
Общим интегралом уравнения (6.16) является функция
.
Отсюда вытекает, что общим интегралом однородного уравнения колебаний будет функция
-
.
(6.17)
Таким образом, функция (6.17) удовлетворяет
уравнению задачи (6.10) и всякое его решение
представимо в виде (6.17). Если функции
и
дважды непрерывно дифференцируемы, то
формула (6.17) даёт классическое решение
однородного уравнения колебаний.
Функции
и
определяются из начальных условий
задачи (6.10). Подставляя (6.17) в начальные
условия, получим
,
, 
,
где штрих означает производную по
полному аргументу. Обозначая аргументы
функций
и
через
и интегрируя второе из равенств, будем
иметь
,
, 
,
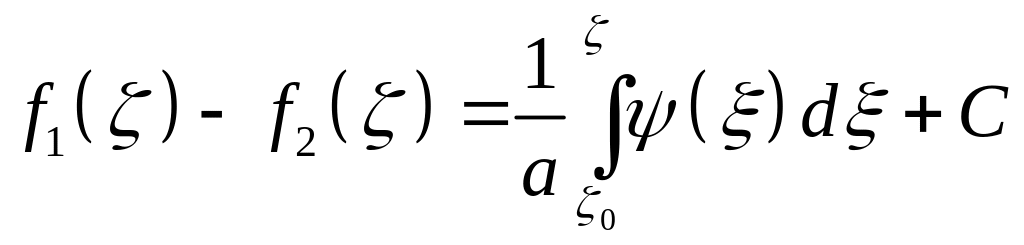где
и
– некоторые постоянные.
Складывая и вычитая два последних равенства, получим
,
,
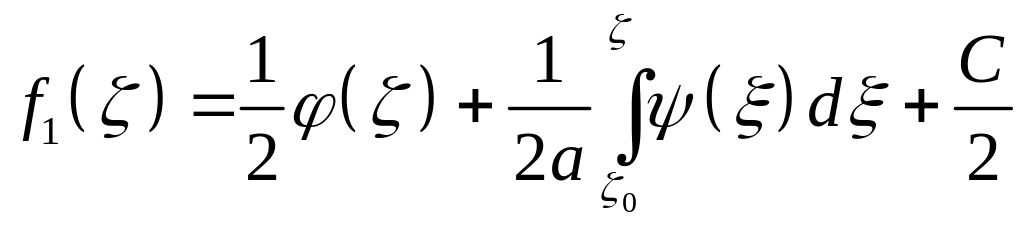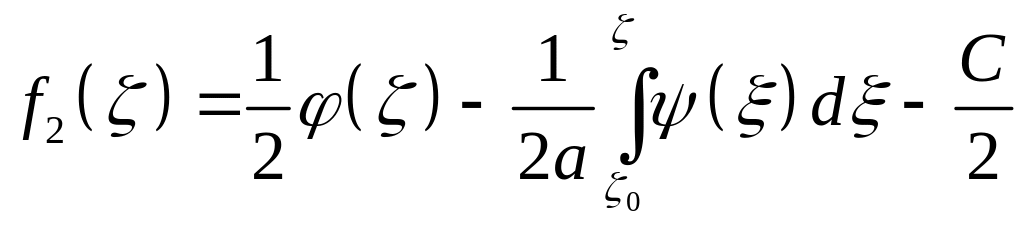и после подстановки
и
в формулу (6.17) придём к формуле Даламбера
(6.14).
Метод распространяющихся волн используется не только для решения задач на неограниченной прямой, но на полупрямой и на отрезке.
Решить начальную задачу на бесконечной прямой:
,
,
;
,
,
.
Решить начальную задачу на бесконечной прямой:
,
,
;
,
,
.
Решить начальную задачу на бесконечной прямой:
,
,
;
,
,
.
Решить начальную задачу на бесконечной прямой:
,
,
;
,
,
.
Решить начальную задачу на бесконечной прямой:
,
,
;
,
,
.
Решить начальную задачу на бесконечной прямой:
,
,
;
,
,
.
На конце полуограниченного стержня укреплена мембрана, оказывающая сопротивление продольным колебаниям стержня, пропорциональное скорости
.
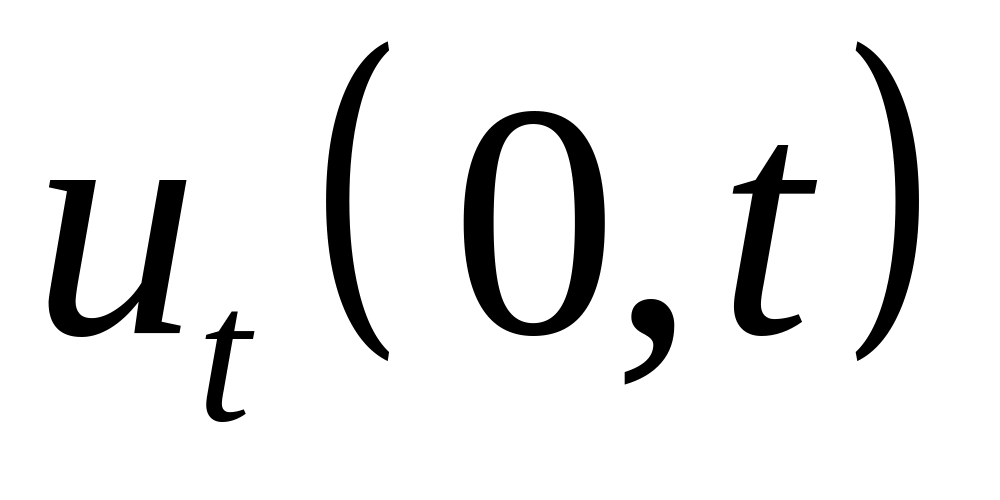Исследовать процесс колебания, если
заданы начальные смещения и
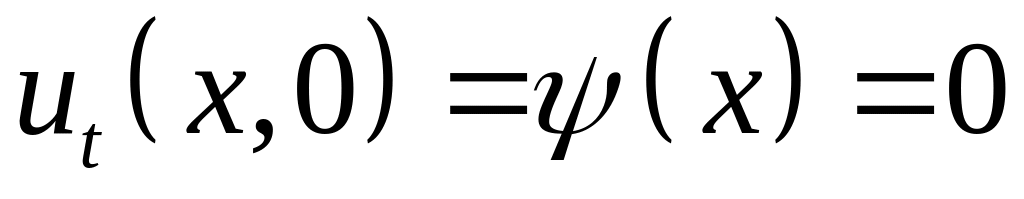.Пусть по неограниченной струне бежит волна
.
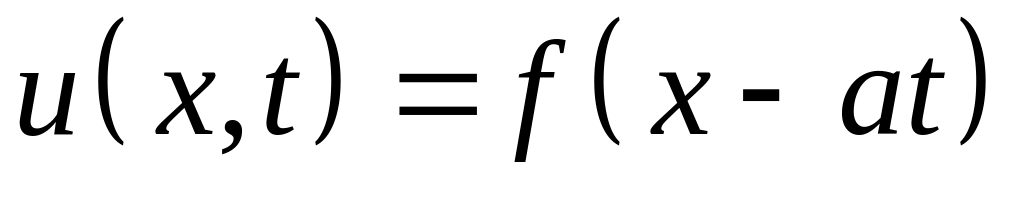Состояние струны в момент
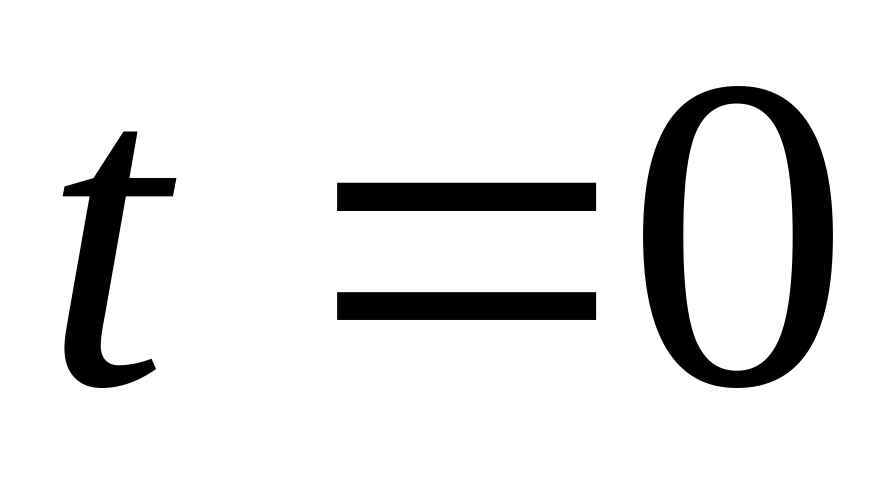принять за начальное и решить уравнение
колебаний при соответствующих начальных
условиях.Пусть в некоторой точке струны подвешен груз массы
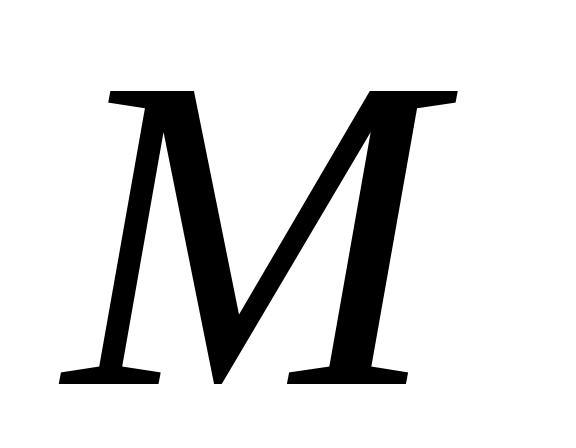и из области
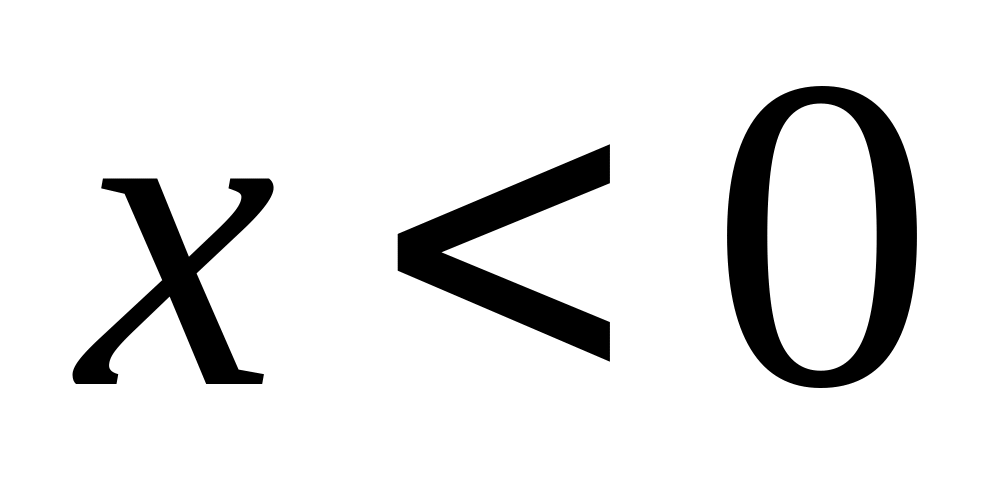бежит волна
.
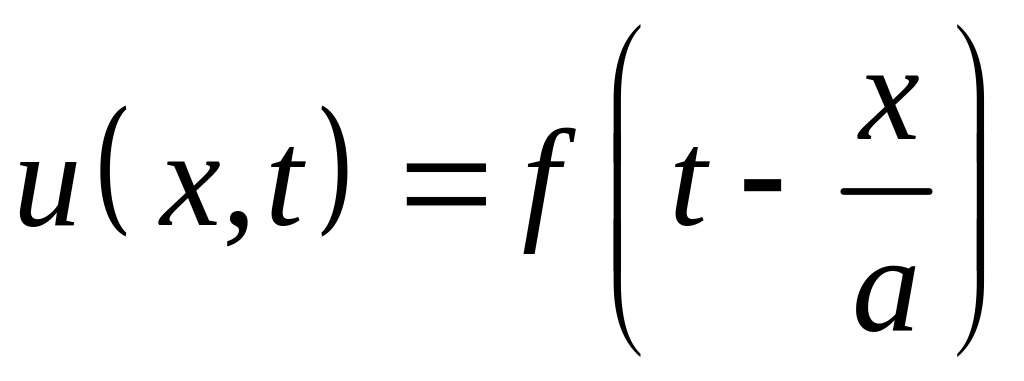Найти выражения для преломленной и отраженной волн.
Решить начально-краевую задачу на полупрямой:
,
,
;
,
,
;
,
.
Решить начально-краевую задачу на полупрямой:
,
,
;
, , ;
, .