Ставропольский государственный университет Кафедра теоретической физики Практическое занятие 5.

Тема: УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА.

УРАВНЕНИЕ КОЛЕБАНИЙ.

Смерек Ю.Л.

Ставрополь – 2009.

Цель: Освоить основные методы решения краевых задач для однородных и неоднородных уравнения колебаний: метод Даламбера и метод разделения переменных. Рассмотреть решение физических задач, приводящих к краевым задачам для уравнений гиперболического типа.

Формы работы:

• Самостоятельное изучение рекомендованной литературы.

• Выполнение коллективных и индивидуальных заданий.

Отчет:

• Ответы на контрольные вопросы.

• Защита результатов выполнения коллективных и индивидуальных заданий.

§ 1. Задачи для уравнений колебаний в ограниченной области с однородными граничными условиями

Рассмотрим начально-краевую задачу с однородными граничными условиями

, , , , , , .

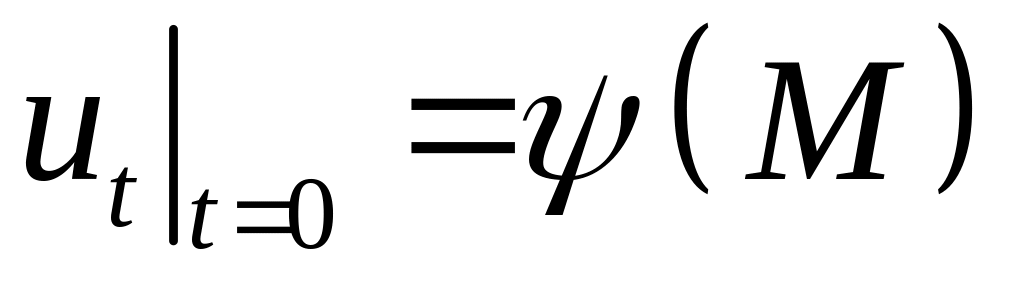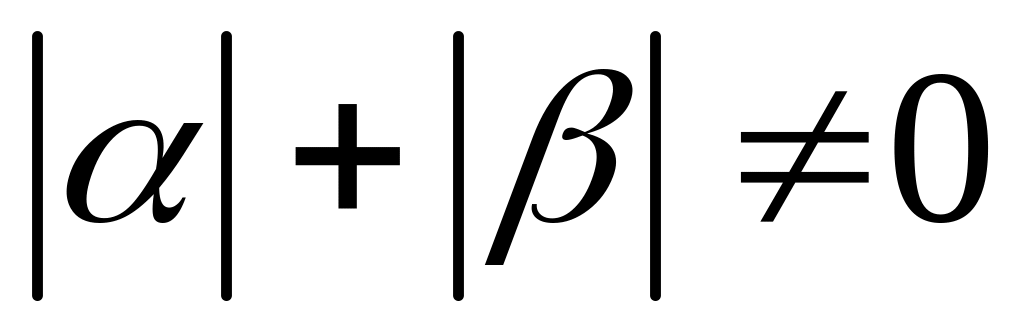(6.1)

Решение этой задачи можно представить в виде разложения

,

коэффициенты которого являются решением задачи Коши

, ,

, , ,

где и – собственные функции и собственные значения соответствующей задачи Штурма-Лиувилля для оператора Лапласа

,	(6.2)
,	(6.3)

, ,

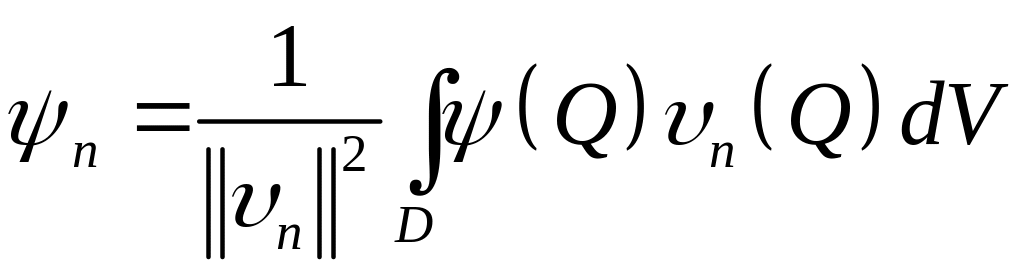– коэффициенты Фурье разложения функций , , по системе собственных функций ,

– квадрат нормы собственной функции.

Решение задачи Коши для функции записывается в виде

,

где – импульсная функция¹.

Таким образом, решение начально-краевой задачи для уравнения колебаний в случае однородных граничных условий записывается в следующем виде:

,

(6.4)

где значения , и определяются формулами (6.2) и (6.3). Первое слагаемое в формуле (6.4) представляет собой решение начально-краевой задачи для однородного уравнения колебаний с неоднородными начальными и однородными граничными условиями, а второе слагаемое – решение начально-краевой задачи для неоднородного уравнения колебаний с однородными начальными и однородным граничным условиями.

Пусть функция имеет вид . Физически это соответствует процессу колебаний объёма под действием периодической силы, распределённой с плотностью .

Предположим, сопротивление отсутствует, в начальный момент времени тело находилось в состоянии покоя и его граница остаётся неподвижной в процессе колебаний. Начально-краевая задача, моделирующая процесс таких колебаний, ставится следующим образом (для определённости рассмотрим случай синусоидальной зависимости от времени):

, ,

, , .

Решение этой задачи представляется формулой (6.4) при , которую мы запишем следующим образом:

,

где

, .

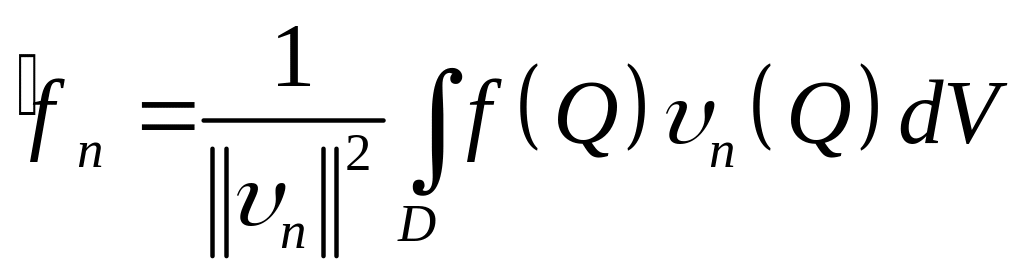(6.5)

Отсюда сразу видно, что если , то . Поэтому если ортогональна к собственной функции , то гармоника номера в объёме не возбуждается, какова бы ни была частота внешней силы.

Введ1м обозначение: . Величины являются собственными частотами области . Вычислим :

.

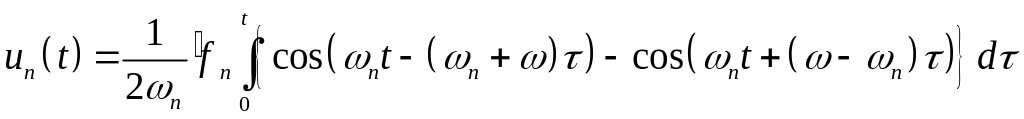Если , то применяя правило Лопиталя², получим

.

Таким образом, коэффициент номера будет неограниченно нарастать со временем (линейно по ) только в том случае, когда и . В этом случае наступает явление резонанса.

Итак, решение исходной задачи имеет вид:

а) если при всех , то

,

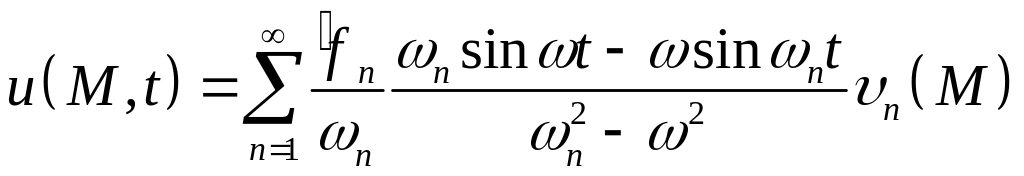(6.6)

где – задано соотношением (6.5);

б) если , то

,

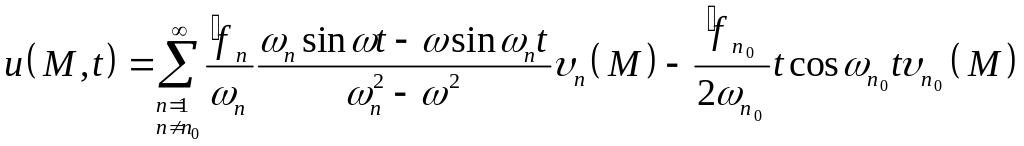(6.7)

значение также определено формулой (6.5).

Ещё раз подчеркнём, что для наступления резонанса, т.е. неограниченного нарастания колебаний со временем под действие внешней периодической силы , необходимо выполнение двух условий:

и .

Рассмотрим примеры решения начально-краевых задач для уравнения колебаний в ограниченных областях.

1. Решить начально-краевую задачу для уравнения колебаний на отрезке :

, , ,

, , .

Решение. Граничными условиями являются однородные граничные условия Дирихле. Поэтому собственными функциями в разложении (6.4) будут собственные функции отрезка с граничными условиями Дирихле

, ,

с квадратом нормы

.

Собственные значения имеют вид

,

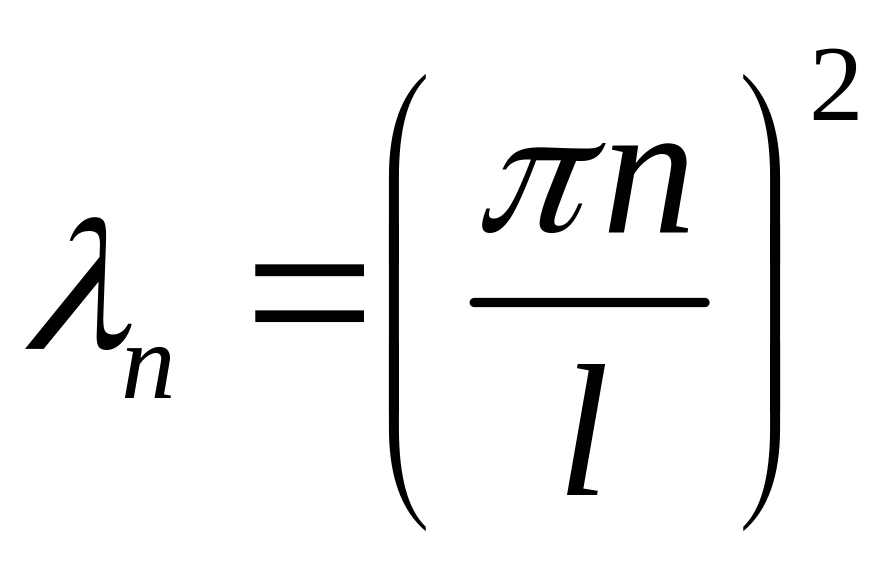Согласно формуле (6.4) общее решение начально-краевой задачи на отрезке с однородными граничными условиями Дирихле для неоднородного уравнения колебаний с неоднородными начальными условиями имеет вид

,

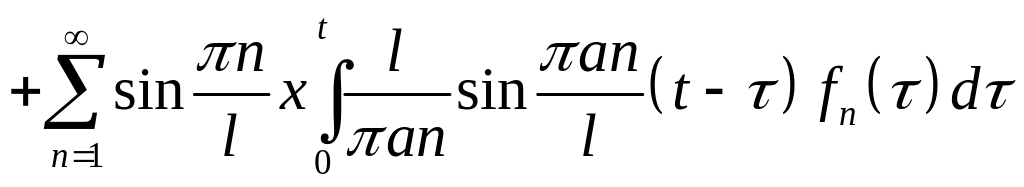(6.8)

где, что следует из формул (6.2) и (6.3), имеем

, , .

(6.9)

Поскольку первое начальное условие однородное, , а из однородности уравнения следует, что . В результате из формул (6.8) и (6.9) получим

,

где

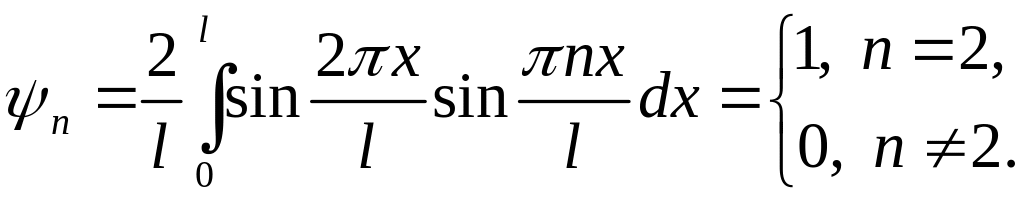
Таким образом,

.

Отметим, что решение задачи представляется в виде одного члена ряда. Это связано с тем, что в качестве второго начального условия выбрана собственная функция , поэтому в силу ортогональности системы собственных функций все коэффициенты , кроме коэффициента , равны нулю.

2. Решить начально-краевую задачу для неоднородного уравнения колебаний на отрезке :

, , ,

, , .

Решение. Воспользуемся формулой (6.8), в которой в силу однородности начальных условий , , а собственными функциями и собственными значениями являются собственные функции и значения задачи Дирихле на отрезке

, , , ,

,

где согласно (6.9)

Следовательно,

.

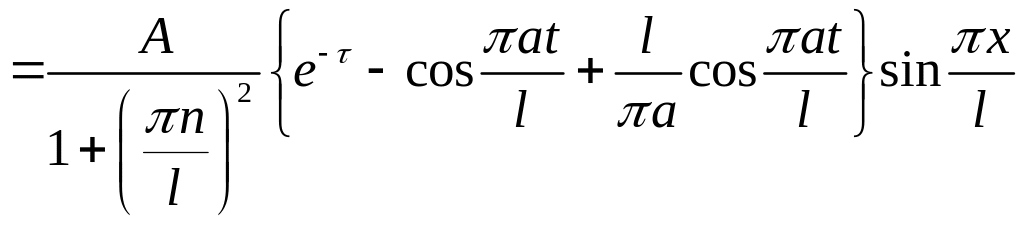Отметим, что, как и в задаче 1, решение представляется одним членом ряда с . Это объясняется тем, что зависимость от координаты в неоднородности уравнения задаётся собственной функцией .

3. Найти процесс колебаний однородной ненагруженной струны длины с закрепленными концами, если начальная скорость струны равна нулю, а начальное отклонение имеет вид

Решение. Пусть в положении равновесия струна расположена вдоль оси между точками и . Поскольку по условию струна однородная, то её линейная плотность постоянна , а в силу того, что рассматриваются малые колебания, постоянным остаётся натяжение .

Начально-краевая задача, описывающая процесс колебаний свободной струны с закрепленными концами, ставится следующим образом:

, , ,

, , .

Решение поставленной задачи записывается с помощью формулы (6.8), в которой , , , , ;

,

Таким образом,

,

где – собственные частоты струны.

Отметим, что в выражении для исчезают слагаемые, для которых , т.е. отсутствуют обертоны, для которых точка является узлом.

Энергия струны равна сумме энергий гармоник. Подсчитаем энергию -й гармоники. Выражение для неё имеет следующий вид:

,

и

.

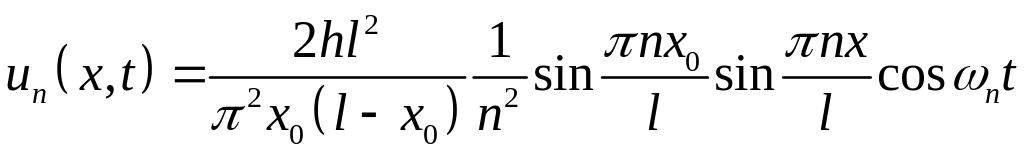Энергия -й гармоники струны состоит из двух слагаемых: кинетической энергии

и потенциальной энергии

.

В процесс колебаний струны происходит постоянная перекачка энергии из потенциальной в кинетическую, причём сумма потенциальной и кинетической энергий остаётся постоянной. При этом, когда кинетическая энергия -й гармоники достигает максимального значения (струна проходит положение равновесия), её потенциальная энергия обращается в нуль, и, наоборот, когда потенциальная энергия -й гармоники достигает максимального значения (струна находится в одном из крайних положений), её кинематическая энергия обращается в нуль. Поэтому

,

где – масса струны.

Из последней формулы вытекает, что энергия обертонов, для которых выполнено условие , равна нулю.