1. Статистические методы оценки качества продуции

Целью работы является изучение теоретических основ и получение практических навыков применения статистических методов при оценке качества продукции.

Задачей работы является практическое применение статистических методов при оценке качества лесопродукции.

1. Теоретическая часть

Используя методические указания [1] следует ответить на следующие вопросы:

1. С какой целью применяют метод проверки статистических гипотез при оценке качества продукции?

2. Какие порядок и правила проверки статистических гипотез?

3. С какой целью и в каком порядке выполняется проверка гипотезы об однородности результатов измерений показателей качества продукции?

4. С какой целью и в каком порядке выполняется проверка гипотезы о математическом ожидании показателя качества продукции?

5. С какой целью и в каком порядке выполняется проверка гипотезы равенства математических ожиданий двух одноименных показателей качества продукции ?

6. С какой целью и в каком порядке выполняется проверка гипотезы о дисперсии контролируемого показателя качества продукции?

7. С какой целью и в каком порядке выполняется проверка гипотезы о дисперсии двух одноименных показателях качества продукции?

8. С какой целью и в каком порядке производится построение доверительного интервала?

2. Практическая часть

Практическая часть состоит из 6 разделов (оценок), выполняемых в приведенной ниже последовательности.

Оценка 1. Проверка гипотезы об однородности результатов измерений показателя качества продукции (выявление грубых ошибок).

Проверку гипотезы об однородности результатов измерений выполняют, например, тогда, когда при контроле какого-либо ПК продукции в выборке несколько результатов наблюдений (измерений) группируются достаточно близко вокруг какого – то значения, а один результат резко отличается от них.

Проверка гипотезы об однородности результатов измерений сводится к исключению грубых ошибок. Грубая ошибка – это заведомо неверный результат измерений.

При анализе данных измерений возможно выявление резко выделяющихся значений измеряемых величин (грубых ошибок). Эти значения должны быть исключены из рассмотрения в самом начале обработки результатов измерений.

Грубая ошибка – наиболее часто результат невнимательности при выполнении измерений. Грубые ошибки возникают и вследствие резкого, непредусмотрительного изменения условий протекания технологического процесса или же в результате описок, неверных записей и т.д.

Наличие грубой ошибки в выборке нарушает характер распределения, изменяет его параметры, т.е. нарушает однородность наблюдений.

В результате статистической обработки выборки установлено, что:

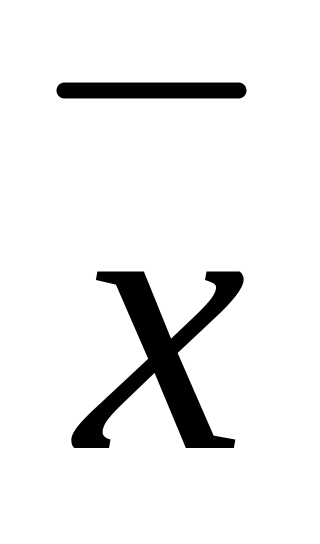• = 26,53 мм;

• S= 0,946 мм;

• Х_min = 24,60 мм;

• Х_max = 28,25 мм.

Проверим, являются ли эти члены выборки грубыми ошибками. Уровень значимости α = 0,05:

1. По формуле U_n =

а по формуле U₁ =

2. Для уровня значимости α = 0,05 и n = 50 находим значения квантеля β = 2,9.

3. U_n = 1,82 < β = 2,9 и U₁ = 2,04 < β = 2,9, следовательно, подозреваемые на грубую ошибку результаты измерений Х_min = 24,60 мм и Х_max = 28,25 мм не являются грубыми ошибками и не исключаются из выборки.

Оценка 2. Проверка гипотезы о математическом ожидании показателя качества продукции (выявление систематической ошибки).

Проверка гипотезы о математическом ожидании (генеральном среднем) показателя качества находит применений при оценке качества продукции, точности работы поточных линий, нормативов времени выполнения операций технологического процесса и др.

1. Рассчитаем наблюдаемое значение статистики

2. Сравним вычисленное значение статистики с табличной величиной (при α = 0,05)

U_набл = 10,12 > Uα/2 = 2,1, следовательно, расхождение между х и Т_с является доказанным, что говорит о наличие систематической ошибке. Следовательно, лесопильная рама нуждается в подналадке, путем устранения смещения наладки.

Оценка 3. Проверка гипотезы равенства математических ожиданий (генеральных средних) двух одноименных ПК продукции (выявление равенства (различия) систематических ошибок).

Применяется в случае сравнения ПК продукции с показателями эталона, либо с ПК сравниваемой продукции от разных производителей, либо на одном и том же потоке при изменении условий течения процесса.

Примем модель 1, считая, что СКО сравниваемых выборок известно.

1. Рассчитаем наблюдаемое значение статистики (у = 26,06, S_y = 0,831)

2. Сравнивая вычисленные значения статистики с его табличной величиной (при α = 0,05), видим, что t_набл = 2,61 > t_; = 2,01, следовательно, нулевая гипотеза отклоняется, на лесопильных потоках производятся доски не одинакового качества.

Т.к. следовательно, качество доски выше на потоке «y».

Оценка 4. Проверка гипотезы о дисперсии контрольного ПК применяется для оценки, находится ли рассеивание значения ПК в допустимых пределах (выявление случайной ошибки).

Проверка гипотезы о дисперсии играет большую роль в управлении качеством продукции, т.к. именно дисперсия характеризует такие важные конструктивные и технологические показатели, как точность работы машин и изготовление продукции, погрешности показания измерительных приборов, ритмичность производства, устойчивость работы автоматических линий и др.

1. Рассчитаем наблюдаемое значение статистики

2. Сравним вычисленное значение с его табличным значением (при α = 0,05, υ = 50 – 1 = 49)

²_набл = 172,03 > ²_a,v = 67, случайная ошибка будет больше нормативной, что ведет к браку за счет случайной ошибки, превышающей 5%. Нулевая гипотеза отклоняется, следовательно, лесопильная рама нуждается в подналадке.

Оценка 5. Проверка гипотезы о дисперсиях двух одноименных показателей качества продукции.

Метод сравнения дисперсии имеет особо важное значение в управлении качеством продукции, так как измеряемая дисперсией величина рассеивания показателя качества характеризует точность работы машин, станков, приборов, технологических процессов в целом, стабильность параметров сырья, технологических режимов и т.п. Метод сравнения дисперсий применяют, когда требуется оценить изменчивость показателей качества (их рассеивание) в зависимости от способа или режима обработки, применяемого оборудования, инструмента или сырья и т.д. Этот метод позволяет обнаружить наличие систематических погрешностей, приводящих к изменению во времени среднеквадратического отклонения.

1. Рассчитаем наблюдаемое значение статистики

2. Сравним вычисленное значение с его табличным значением (при α = 0,05, υ₁ = n₁ – 1 = 50 – 1 = 49, υ₂ = n₂ – 1 = 50 – 1 = 49)

F_набл = 1,3 < F_ = 1,46, следовательно, можно считать вариабельность одинаковой.

Оценка 6. Построение доверительного интервала.

Так как при механической обработке древесины имеет место, как смещение наладки, так и рассеивание значений ПК, то для оценки соответствия значений ПК установленным требованиям строят доверительный интервал, как для величины , так и для величины s по ниже изложенной методике.

Метод построения доверительного интервала находит применение при оценке надежности оборудования (технологических операций) и технологических процессов (ТП) по значениям показателей качества продукции.

Целью оценки надежности по показателю качества продукции является:

• определение возможности применения ТП для изготовления продукции с определенными значениями показателей качества;

• оценка изменения точностных характеристик ТП во времени и определение их соответствия требованиям НТД;

• получение информации для регулирования ТП (операций).

  1. Для α = 0,05 и К = n – 1 = 49, находим значения квантеля распределения Стьюдента t_y = 2,01

  2. Рассчитаем величину 

3. Запишем доверительный интервал для Х

Для построения доверительного интервала для Х используют модуль DS – «Описательная статистика» (среднее значение, стандартное отклонение) пакета анализа «AtteStat» среды Excel 2007. Результаты расчётов по показателю качества «Толщина доски» приведены в разделе 7.2.2. (подраздел 2, выделено зелёным цветом).

Сравнивания интервалы видим, что они совпали.

Сравнивая значение T_с = 25,8 мм с интервалом, видим, что оно не попадает в интервал, следовательно, имеет место систематическая ошибка, т.е. процесс не центрирован, М_е не равно 0, оборудование нуждаются в подналадке (такой же вывод получен при выполнении оценки №2).

4. Запишем доверительный интервал для S. Для К = n – 1 = 49 находим, используя интерполирование - ²₁ = 71 и ²₂ = 33.

Для построения доверительный интервал для Х используют модуль DS – «Описательная статистика» (среднее значение, стандартное отклонение) пакета анализа «AtteStat» среды Excel 2007. Результаты расчётов по показателю качества «Толщина доски» приведены в разделе 7.2.2. (подраздел 2, выделено зелёным цветом).

.

Сравнивания интервалы видим, что они близки по величине.

Сравнивая [₁] = 0,51 мм (см. раздел 7.2.2, подраздел 4.2), соответствующее нормативной доле дефектной продукции в 5%, с интервалом, видим, что оно не попадает в интервал I_S, следовательно, рассеивание (случайная ошибка) показателя качества больше нормативного, т.е. доля дефектной продукции будет больше нормы, с которой определена СКО; лесорама нуждается в подналадке.