Содержание отчета

1 Наименование и цель работы.

2 Временные диаграммы сигналов.

3 Исходные данные для расчета.

4 Результаты расчетов.

5 Спектральные диаграммы сигналов.

6 Ответы на контрольные вопросы (по заданию преподавателя).

7 Выводы по работе.

Контрольные поросы

1 Сравните спектральные диаграммы исследуемых Вами сигналов со спектральной диаграммой одиночного прямоугольного видеоимпульса. Проведите анализ.

2 Чему равна спектральная плотность неопределенного интеграла?

3 Как связаны скалярные произведения сигналов и их спектральных плотностей?

Краткие теоретические сведения

Спектральная плотность – это комплексно-значимая функция частоты, одновременно несущая информацию, как об амплитуде, так и о фазе элементарных синусоид.

Спектральная плотность и сигнал связаны между собой парой преобразований Фурье:

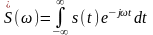(2.1)

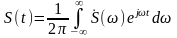(2.2)

Поскольку для представления спектров непериодических сигналов используются интегральные преобразования Фурье, эти спектры сплошные.

Спектральная плотность может быть представлена в виде:

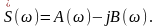
Вещественная часть спектральной плотности есть чётная функция частоты:

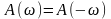
Мнимая часть спектральной плотности есть нечётная функция частоты:

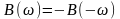
Если записать спектральную плотность в показательной форме, то можно выделить её модуль и аргумент:

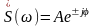
Модуль спектральной плотности называется амплитудным спектром сигнала:

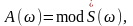
а аргумент спектральной плотности – фазовым спектром сигнала.

_.

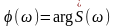Пара преобразований Фурье имеет фундаментальное значение в теории электросвязи, так как многие характеристики сигналов связаны между собой этими преобразованиями.

Все свойства спектральной плотности объединены в основных теоремах о спектрах.

При выполнении задания 2 применяют следующие теоремы о спектрах.

1. Линейность.

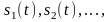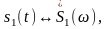
Если имеется некоторая совокупность сигналов причём ,…, то взвешенная сумма сигналов преобразуется по Фурье следующим образом:

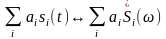(2.3)

Здесь 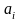- произвольные числовые коэффициенты.

2. Теорема о сдвигах.

_{Предположим, что для сигнала} известно соответствие 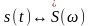. Рассмотрим такой же сигнал, возникающий на 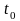секунд позднее. Принимая точку за новое начало отсчёта времени, обозначим смещённый сигнал как 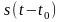. Введём замену переменной: 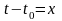. Тогда , _.

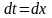_{В результате получаем:}

(2.4)

Модуль комплексного числа 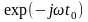при любых равен 1, поэтому амплитуды элементарных гармонических составляющих, из которых складывается сигнал, не зависят от его положения на оси времени. Информация об этой характеристике сигнала заключена фазовом спектре.

3. Теорема о спектре производной и неопределённого интеграла.

Пусть сигнал и его спектральная плотность заданы. Будем изучать новый сигнал 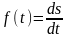и поставим цель найти его спектральную плотность .

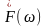По определению:

(2.5)

Преобразование Фурье – линейная операция, значит, равенство (2.5) справедливо и по отношению к спектральным плотностям. Получаем по теореме о сдвигах:

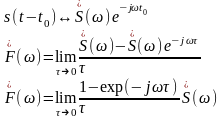
(2.6)

Представим экспоненциальную функцию рядом Тейлора:

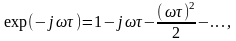
Подставляя этот ряд в (2.6) и ограничиваясь первыми двумя числами, находим

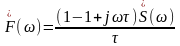
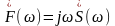(2.7)

Итак, дифференцирование сигнала по времени эквивалентно простой алгебраической операции умножения спектральной плотности на множитель 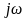. Поэтому говорят, что мнимое число является оператором дифференцирования, действующим в частотной области.

Вторая часть теоремы. Рассмотренная функция 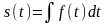является неопределённым интегралом по отношению к функции . Интеграл это есть , значит 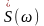- его спектральная плотность, а из формулы (2.7) равна:

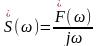(2.8)

Таким образом, множитель 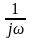служит оператором интегрирования в частотной области.

Полезным для расчетов является фильтрующее свойство δ-функции, которое заключается в следующем. Интеграл от произведения некоторой функции u(t) на δ-функцию равен значению этой функции при t, для которого δ(t) ≠ 0.

Например:

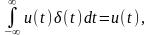
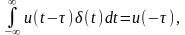(2.9)

Согласно (2.1) спектральную плотность δ-функции можно представить в виде:

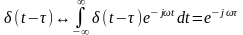(2.10)

На основании (2.8) и (2.9) и свойства линейности спектр суммы прямоугольных импульсов может быть получен суммированием спектров производных фронтов импульсов, и делением этой суммы на jω с учетом того, что для фронта прямоугольного импульса его производная равна