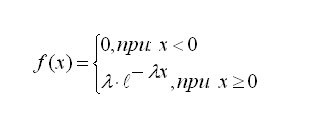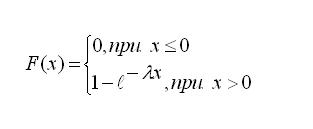2. Показательное (экспоненциальное) распределение

Экспоненциально распределенной называется такая случайная величина, для которой плотность вероятности имеет вид

(33)

Здесь - параметр распределения.

Проверим, что это плотность распределения:

, что и требовалось доказать.

Функция распределения вероятностей показательного распределения имеет вид

(34)

Графики f(x) и F(x) представлены на рис. 5.

Рис. 5. Графики плотности вероятности и функции вероятности для

показательного (экспоненциального) распределения

Найдём числовые характеристики показательного распределения:

*) Интегрируем по частям:

Итак, если непрерывная случайная величина имеет показательное распределение, то её числовые характеристики определяются по формулам:

(35)

Найдём вероятность попадания случайной величины Х, распределённой по показательному закону, в интервал (a,b). Используя формулы (3) и (34), получаем

(36)

Пример 3.2.1. Случайная величина Т – время работы радиолампы имеет показательный закон распределения. Найти вероятность того, что лампа проработает не менее 800 часов, если среднее время работы радиолампы 400 часов.

Решение. Имеем: M(T) = 400, значит, (см. формулы (35)) . Искомая вероятность

Ответ: 0,135.

Показательный закон распределения – единственный из законов распределения, который обладает свойством «отсутствия последействия» (то есть если промежуток времени Т уже длился некоторое время , то показательный закон распределения остаётся таким же и для оставшейся части Т - промежутка). Считают, что время жизни атома имеет показательное распределение Свойство отсутствия последействия имеет следующий смысл: каков бы ни был настоящий возраст, оставшееся время жизни не зависит от прошлого и имеет то же самое распределении, что и само время жизни.

Использование показательного распределения в математических моделях реальных явлений обычно связано именно с этим характерным свойством.

Показательное распределение используется в приложениях теории вероятностей, особенно в теории массового обслуживания (ТМО), в физике, в теории надежности. Оно используется для описания распределения случайной величины вида: длительность работы прибора до первого отказа, длительность времени обслуживания в системе массового обслуживания и так далее.

Рассмотрим, например, непрерывную случайную величину Т - длительность безотказной работы прибора. Функция распределения случайной величины Т, то есть F(t) = P{T < t}, определяет вероятность отказа за время длительностью t. Значит, вероятность безотказной работы за время t равна R(t) = P{T > t} =1 – F(t). Функция R(t) называется функцией надёжности.

Случайная величина Т часто имеет показательное распределение. В этом случае функция надёжности имеет вид R(t) = 1- F(t) = 1 – (1 - , то есть интенсивность отказов, то есть среднее число отказов в единицу времени.

Пример 3.2.2. Время обслуживания клиента на станции технического обслуживания имеет показательное распределение, причём чем дольше обслуживают в среднем каждого клиента, тем меньше значение параметра .