Контрольные вопросы

1. Почему тесты на неосознанные моторные реакции являются более надежными, чем тесты на осознанные реакции?

2. Каковы причины возможного расхождения результатов тестирования осознаваемой и неосознанной моторики?

3. Почему исследование морфологических признаков тела следует считать более убедительным при установлении диссимметрии, чем тестирование моторики?

4. Объясните механизм выявления ведущего глаза согласно пробе Розенбаха.

Литература

1. Брагина Н.Н., Доброхотова Т.А. Функциональная асимметрия человека. М.: Медицина, 1981 . - 225 с.

2. Гильде В. Зеркальный мир. М.: Мир, 1982. - 120 с.

3. Саган К. Драконы Эдема. М.: Знание, 1986. - С. 159-196.

Практическая работа № 35

БИФУРКАЦИОННАЯ ДИНАМИКА СИСТЕМ

Раздел программы: Новые направления науки о самоорганизации

Необходимые предварительные знания: – – –

Теоретическая часть

Полученные еще в прошлом веке выдающимся французским математиком А. Пуан­каре (1854–1912) результаты анализа решений некоторых дифференциальных уравнений (т.н. бифуркация решений), развитые затем отечественным ученым – физиком А.А. Андроновым (1901–1952) в области теории нелинейных колебаний, нашли неожиданное применение во 2-ой половине XX в. в науке о самоорганизации. Основополагающей работой в этом направлении стало классическое исследование видного английского математика А.М. Тьюринга (1912–1954) под названием “О химической основе морфогенеза”, опубликованное в 1952 г. В нем математически было показано, что при определенных условиях взаимодействие химической реакции и чисто физического процесса диффузии приводит к возникновению стационарной пространственной неоднородности концентраций вещества, т.е. структуры. Спустя несколько десятилетий выводы Тьюринга были блестяще подтверждены в биологических экспериментах. Более того, круг явлений, описываемых в рамках подхода Тьюринга, оказался очень широк: кроме биологических процессов сюда вошли некоторые химические, экологические процессы, а также процессы, относящиеся к гидродинамике, физике плазмы и т.д. В настоящее время теория бифуркаций вышла далеко за рамки естествознания и применяется в исторической науке, социологии, педагогике, медицине и других областях.

Ход работы

Примечание: Выполнение предусмотренных в работе вычислений намного ускоряется при использовании программируемого калькулятора. Программа расчетов весьма проста и здесь не приводится.

1. Уясните модельную ситуацию, предложенную отечественным исследователем Л.П. Кадановым.

Пусть на изолированном острове летом выводятся насекомые численностью x_i, которые кладут яйца и умирают. Из яиц на следующий год выводятся новые насекомые численностью x_i+1. Очевидно, численность потомства x_i+1 должна зависеть от численности родительского поколения x_i и от каких-то дополнительных факторов. Эта зависимость учитывается уравнением:

x_i+1 =  x_i (N – x_i),

где 0 – некоторый параметр (т.е. постоянная в условиях рассмотрения величина), N – максимально возможная численность популяции (обоснуйте это!).

Для унификации уравнения численность популяции нормируют по отношению к предельной величине, что математически оформляется делением обеих частей равенства на N ²:

где

Проделайте указанные преобразования и убедитесь в правильности записи унифицированного уравнения. В дальнейшем изложении штрихи будем опускать.

2. Проанализируйте унифицированное уравнение. Оно решается путем подстановки значений x_i ( ) с дальнейшим расчетом x_i+1, которое вновь считается исходным x_i и т.д. Такой последовательный расчет в математике называют рекуррентным (в переводе с латинского – “возвратным”). Однако результаты рассматриваемого расчета в данной задаче существенно зависят от величины параметра , называемого также параметром скорости роста.

Так, для небольших  (01) выполняется x_i0, независимо от выбора начального значения x₀. Убедитесь в этом, задав x₀ и  в соответствии с вышеуказанными интервалами. Результаты расчетов отразите в таблице 1, указав сверху нее значение .

= ____________ Таблица 1

x0	x1	x2	x3	x4	x5	x6	x7	x8

Анализ табличных результатов показывает, что при малых  популяция вымирает.

3. Продолжите анализ унифицированного уравнения, задав  большее, а именно 13. Результаты расчетов отразите в таблице 2, оформив ее по аналогии с таблицей 1.

Как можно увидеть, в данном случае популяция не вымирает (ср. п. 2), а стремится по численности к некоторому предельному значению x^*. Этот предел для каждого  может быть рассчитан аналитически путем решения уравнения:

x^*= x^*(1– x^*).

Объясните, почему справедливо такое уравнение. Оно является квадратным и имеет два решения: .

Первое решение реализуется (т.е. существует устойчиво) при малых  (01), а второе для 1, т.к. по условиям задачи должно быть . Для , очевидно, характерен годичный цикл численности.

4. Задайте  еще большее (33,4) и рассчитайте динамику популяции. Результаты расчета отразите в таблице 3, аналогичной по форме таблице 1. Как можно увидеть, в этом случае динамика численности заметно усложняется (ср. п. 3). А именно возникают два ее предельных (стационарных) значения, причем сама численность колеблется, попеременно приближаясь то к одному, то к другому пределу. В итоге будет наблюдаться ритмичность колебаний численности с периодом 2 года.

5. Таким образом, характер решения унифицированного уравнения численности популяции существенно зависит от величины параметра , входящего в уравнение. Для “малых”  стационарное значение равно 0, для “средних”  – оно ненулевое, для “больших”  возникают два стационарных состояния. Последняя ситуация и называется бифуркацией решения (и, соответственно, динамического поведения системы). Слово “бифур­кация” в переводе с латинского означает раздвоение, разветвление. В нашем случае она возникает, когда параметр  достигает первого критического значения ₁=3.

Примечание: Строго говоря, первая точка бифуркации соответствует ₀=1. Однако из двух значений x^* (см. п. 3) одно ( ) становится неустойчивым и не реализуется.

М

0 1 3 3,4 3,54 3,56 3,57



x_s

0,8

0,6

0,4

0,2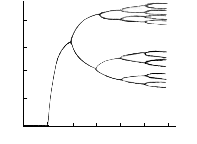

ожно показать, что второе критическое значение ₂=3,4 соответствует раздвоению каждой из ветвей решения, т.е. стационарных значений становится не 2, а 4. При этом возникает четырехстадийный цикл колебаний численности, т.е. четырехлетняя периодичность. Сле­дую­щее критическое значе­ние ₃=3,54 приводит к вось­мистадий­ному циклу, затем появ­ля­ют­­ся 16, 32, 64 и т.д. вет­вей. Соответствующие кри­ти­­чес­кие значения  очень ма­ло отличаются друг от друга. Наконец, при _ 3,57 пе­рио­дичность изменения чис­лен­ности исчезает (ветви ре­шений сливаются, а период повторения можно условно считать бесконечным). Нас­тупает хаотизация динамики (т.н. дина­ми­ческий, или де­тер­миниро­ван­ный хаос). На рисунке приведен сложный гра­фик зависимости стационарных сос­тояний числен­нос­ти от пара­метра скорости рос­та, рассчитан­ный с помощью ЭВМ.

6. Рассмотренная в п.п. 1–5 математическая модель является далеко не единственной, которая приводит к каскаду бифуркаций удвоения периода при изменении некоторого параметра, входящего в уравнение. В самом общем случае такая задача была впервые исследована американским математиком М. Фейгенбаумом в 1978 г. Разработанную им теорию называют теорией универсальности Фейгенбаума. Полученные в ней закономерности оказались общими для широкого класса гидродинамических, механических, электрических, биологических и др. систем.

Резюме

Теория бифуркаций позволяет раскрыть важные закономерности динамического поведения систем различной природы, в том числе – переход от упорядоченного поведения к хаотическому и обратно.

Контрольные вопросы

1. Какие биологические обоснования можно привести для введения величины N в исходное уравнение? Ответ поясните.

2. Уравнение динамики популяции, рассмотренное в данной работе, называется логистическим. Нет ли здесь противоречия с аналогичным названием в практической работе “Моде­лирование динамики популяций”, часть 1?

3. Какова динамика популяции при x₀=0? при x₀=N?

Литература

1. Шелепин Л.А. Вдали от равновесия. М.: Знание, 1987 (сер. “Физика”, № 8). – С. 41–51.

2. Ахромеева Т.С. и др. Парадоксы мира нестационарных структур. М.: Знание, 1985 (сер. “Математика, кибернетика”, № 5). – С. 18–29, 41–48.

Практическая работа № 36

ТЕОРИЯ КАТАСТРОФ В ЕСТЕСТВОЗНАНИИ

Раздел программы: Новые направления науки о самоорганизации.

Необходимые предварительные знания: Исследование функций на экстремум. Уравнение Ван-дер-Ваальса.

Теоретическая часть

Появление теории катастроф относят к началу 70-х гг. XX в., когда были опубликованы труды французского математика Рене Тома и, в частности, основополагающая его работа “Струк­турная устойчивость и морфогенез” (1972). В ней результаты новой теории применялись к решению проблемы биологического структурообразования. Принятое название теории также введено Р. Томом, поэтому последнего считают “отцом” теории катастроф. Однако корни этой теории простираются в глубь столетий и исходят из работ И. Ньютона (1642–1727), Л. Эйлера (1707–1783), Ж.-Л. Лагранжа (1736–1813), У.Р. Гамильтона (1805–1865) и, особенно, русского ученого А.М. Ляпунова (1857–1918) и француза А. Пуанкаре (1854–1912) по теории устойчивости динамических систем. В XX в. еще до публикации вышеупомянутой работы Р.Тома как им сами, так и другими математиками и физиками (Х. Уитни, А.А. Андроновым, В.И. Арнольдом и др.) также были получены результаты, заложившие основу теории катастроф. Эта теория позволяет чисто математическим путем описать, объяснить и предсказать разнообразные скачкообразные переходы динамических систем произвольной природы из одного устойчивого состояния в другое. В настоящее время благодаря универсальным возможностям теорию катастроф применяют в различных разделах физики, в космологии, биологии, психологии, социологии, экономической науке и т.д.