5. Уравнения, решаемые с помощью представления левой части уравнения в виде суммы неотрицательных слагаемых.

Пример 1.

Решить в целых числах уравнение:

Решение:

Т.к. и не принадлежат , то уравнение не имеет решений в целых числах.

Ответ: нет решений.

Пример 2. Решить уравнение в целых числах:

Решение:

Уравнение приводится к виду .

Отсюда имеем , а так как - целое число, то (x может быть только равен 0, 1, -1.

Легко увидеть, что только возможен.

Тогда (у и .

Ответ:

Пример 3.

Решить уравнение в целых числах:

Указание: преобразовать уравнение к виду

Ответ: (0, 0), (1,0), (0,1), (2,1), (1,2), (2,2).

6. Использование свойств простых чисел.

Пример 1.

Решить уравнение в натуральных числах:

Решение:

(*)

взаимно-простые, значит, равенство (*) возможно в 3 случаях.

а) б) в)

a) Нет решений, т.к. , б) в)

Ответ: (11;20), (100;1).

Пример 2.

Решить уравнение в простых числах.

Решение:

Так как и простое, т.е. нечетное, то – четное, т.е. .

Уравнение имеет в простых числах единственное решение Иначе: при нечетном, простом число кратно 3, т.е. не является простым числом. А четным быть не может (кроме ), т.к. должен быть простым числом.

Ответ:

Пример 3.

Решить уравнение в простых числах:

Решение:

Из и простоты получаем либо , либо . У этих систем решений в простых числах нет. Действительно, в первом случае имеем , откуда . Во втором случае имеем , поэтому если то – составное (т.к. тогда – целое, большее 1). В случае имеем , а при

Ответ: решений нет.

Пример 4.

Решить уравнение в простых числах:

Решение:

Из имеем , , где - целое. При y и z – два четных числа и они не могут быть одновременно простыми: Если , то , – два последовательных нечетных числа, значит одно из них делится на 3, тогда либо , либо . При , – не простое.

Ответ:

Пример 5.

Решить уравнение в простых числах

.

Решение:

Т.к. - четное число, то – нечётное, и потому число делится на 4. Следовательно, - четное число, и поскольку и должны быть простыми числами, то , а потому .

Ответ:

7. Учет четности и нечетности выражений.

Пример 1.

Доказать, что не существует решений у уравнения:

+ = 13

Решение:

Т.к. – четное, то нечетное. Корень из нечетного числа – число нечетное.

Аналогично и - нечетное число. Сумма двух нечетных чисел четно, т.е. в левой части мы имеем число четное, а в правой – нечетное.

Ответ: решений нет.

Пример 2.

Найти все пары простых чисел и , которые удовлетворяют уравнению

Решение:

1. Если хотя бы одно из чисел или четное, то справа будет стоять число четное, при этом, стоящее слева тоже обязано быть четным, а это возможно только в том случае, когда только одно из чисел четно.

2. Пусть (это единственное простое четное число), тогда непосредственно, решив биквадратное уравнение относительно , находим = 3.

3. Пусть =2, непосредственно убеждаемся, что в этом случае натуральных значений , удовлетворяющих уравнению, не существует.

4. Если и – нечетные числа: 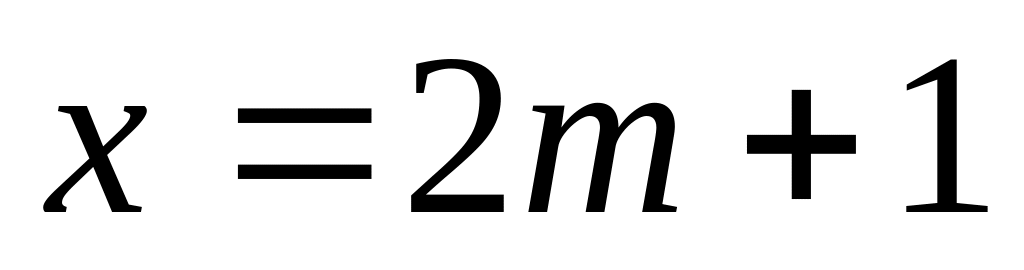и 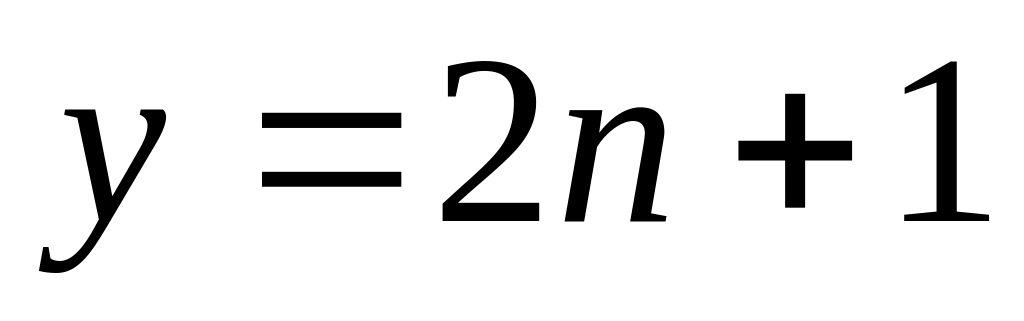, то левая часть первоначального уравнения при делении на 4 дает в остатке 3, при этом правая часть делится на 4 с остатком 1. Следовательно, не существует нечетных простых чисел, удовлетворяющих данному уравнению.

Ответ: .

Пример 3.

Решить систему уравнений в целых числах

Решение:

Если , , и удовлетворяют уравнениям системы, то – нечетное число.

Так как квадрат четного числа есть четное число, то – число нечетное:

Используя это представление для числа , получим , т.е. - четное число, значит и четное: . Число x = y + 7z нечетное.

Поэтому нечетное: . Из первого уравнения системы теперь следует, что – 8k = 7(z ) = 7(2y + 1) = 7(4y + 4y + 1).

Отсюда , что для целых чисел невозможно.

Ответ: решений нет.

Пример 4.

Решить в целых числах уравнение:

Решение:

Если и оба нечетны или одно из них нечетно, то левая часть уравнения есть нечетное число, а правая – четное. В этом случае решений нет.

Если же и , то 8 ,

т.е. 2(2 + 2 - 3 ) , что невозможно ни при каких целых и .

Ответ: решений нет.

Пример 5.

Доказать, что уравнение не имеет решений в целых числах:

Доказательство:

Так как -четное число, а 7 – нечётное, то должно быть нечетным, т.е. - нечетное. Пусть тогда данное уравнение можно переписать в виде (*)

Отсюда видно, что должно быть четным. Пусть тогда равенство (*) примет вид: что невозможно, т.к. число - чётное, а разность двух чётных чисел не может быть равна нечетному числу. Таким образом, данное уравнение не имеет решений в целых числах.

Пример 6.

Доказать, что уравнение не имеет решений в целых числах:

Решение:

Так как правая часть уравнения – нечетное число, то и левая часть должна быть нечетным числом. Поэтому или , или меньше 2.

Пусть для определенности , т.е.

Правая часть последнего равенства не делится на 5, а потому , но ни одно из целых чисел, которые удовлетворяют этому неравенству, не служат решением данного уравнения.

Итак, данное уравнение не имеет решений в целых числах.