Решение уравнений в целых числах Введение
Теория решения уравнений в целых числах является классическим разделом математики.
В ней не приходится писать сложные и громоздкие формулы, а необходимо проводить аккуратные рассуждения, базирующиеся на определенных понятиях теории чисел и связанные в стройную логическую конструкцию.
В рамках этой теории можно дать исчерпывающее решение рассматриваемого класса задач с четко описанным алгоритмом получения ответа.
Конкретные задачи такого рода были решены еще в Древнем Вавилоне около 4 тысяч лет назад. Древнегреческий мыслитель Диофант, который жил около 2 тысяч лет назад, в своей книге «Арифметика» решил большое количество уравнений в целых числах и в сущности описал общие полходы их решения.
Уравнения в целых числах – одна из древнейших математических задач, не потерявшая своей актуальности и сегодня. Алгебраические уравнения или системы уравнений с целыми коэффициентами, имеющие число неизвестных, превосходящее число уравнений, когда стоит задача найти целые или рациональные решения называются диофантовыми или неопределенными уравнениями.
Это пособие имеет целью раскрыть основные приемы решения диофантовых уравнений. Рассмотрим предварительно некоторые теоретические сведения, способствующие решению.
II. Решение нелинейных уравнений.
Одной из главных идей решения нелинейных уравнений в целых числах является ограничение перебора. Для этого могут использоваться различные подходы: разложение на множители, изучение остатков от деления на какое-то число, учет четности или нечетности числа и другие.
Выделим следующие группы нелинейных уравнений:
Уравнения, решаемые с помощью разложения на множители.
Суть метода: Сначала первоначальное уравнение путем группировки слагаемых и вынесения общих множителей приводится к виду, когда в левой части уравнения стоит произведение сомножителей, содержащих неизвестные, а справа стоит некоторое число.
Рассматриваются все делители числа, стоящего в правой части уравнения, затем решается система и выводится ответ.
Пример 1.
Решить
в натуральных числах уравнение:
Решение:
Представить 2001 в виде произведения двух разных натуральных чисел можно тремя различными способами:
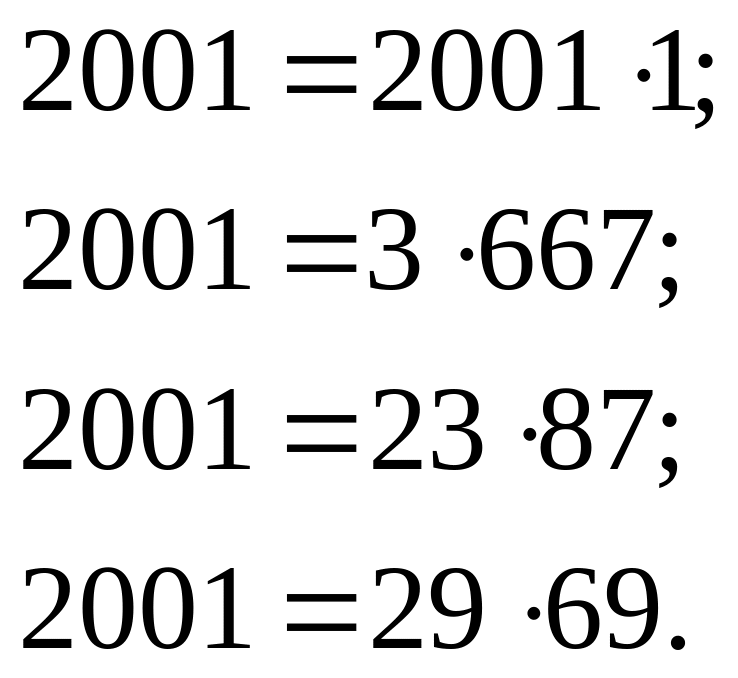
Т.к.
то
,
отсюда
или
,
или
,
или
отсюда
или
, или
, или
Ответ: (1001;1000); (335;332); (49;20); (55;32)
Пример 2.
Решить в целых числах уравнение:
Решение:
отсюда
или
следовательно
или
Ответ: (2;1), (0;1).
Пример 3.
Решить в целых числах уравнение
Решение:
или
или
или
или
или
или
Т.к.
и
,
то решениями уравнения являются пары
Ответ:
Пример 4.
Решить уравнение в целых числах:
Решение:
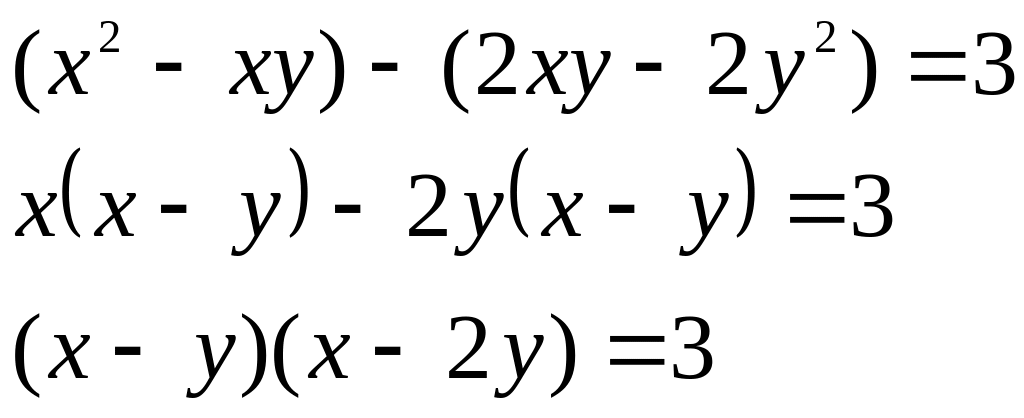
Ответ:
Пример 5.
Решить в целых числах уравнение
Решение:
Перенесем все члены уравнения в левую часть и к обеим частям полученного уравнения прибавим (-1):
2) Записав соответствующие системы уравнений и решив их, получим решение исходного уравнения.
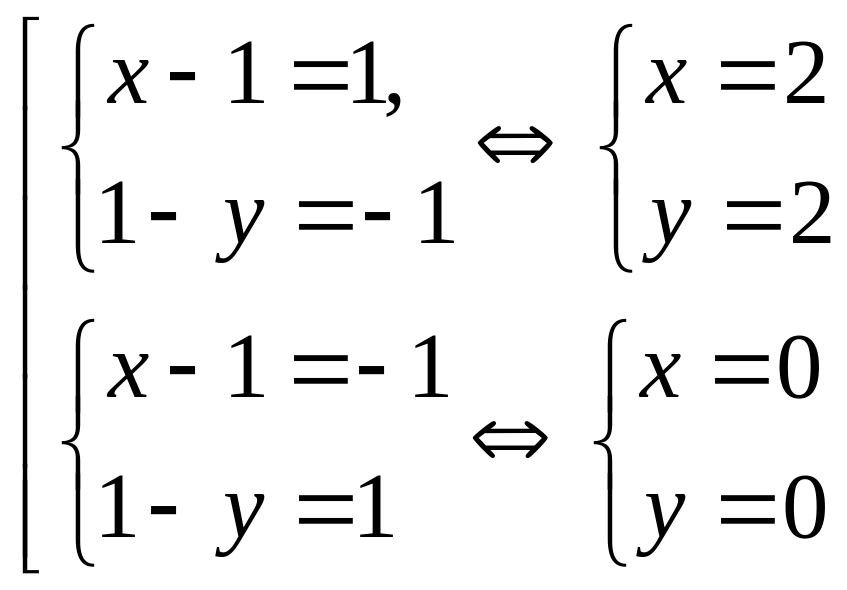Ответ:
(0;0), (2;2).
Пример 6.
Решить уравнение в натуральных числах
Решение:
Преобразуем уравнение к виду
Учитывая,
что
,
получим системы уравнений
1)
5)
2)
6)
3)
7)
4)
8)
Ответ:
